Exercícios Classificação dos estados

Nos exercícios abaixo, sempre que necessário, considere $(X_n{)}_{n\ge 0}$$(X_n)_{n\geq 0}$ uma cadeia de Markov sobre o conjunto de estados $S$$S$ com transições $P$$P$ e distribuição inicial $\lambda$$\lambda$. A v.a. $T_j$$T_j$ é o tempo da primeira visita a $j$$j$ e $N_j$$N_j$ é o número de visitas a $j$$j$ a partir do instante $1$$1$. Alguns exercícios podem exigir a Propriedade Forte de Markov, deixe explícito quando usar essa propriedade.

1. Considere a cadeia de Markov em $\{1,2,3,4\}$$\{1,2,3,4\}$ com matriz de transição

   $$\begin{array}{c}P=\left(\begin{array}{cccc}0& p& 0& 1-p\\ 1-p& 0& p& 0\\ 0& 1-p& 0& p\\ p& 0& 1-p& 0\end{array}\right),0\le p\le 1.\end{array}$$

   Classifique os os estados.

2. Considere a cadeia de Markov com espaço de estados $S=\{1,2,3\}$$S = \{1,2,3\}$ e matriz de transição

   $$\begin{array}{c}P=\left[\begin{array}{ccc}0.7& 0.2& 0.1\\ 0.3& 0.5& 0.2\\ 0.2& 0.4& 0.4\end{array}\right]\end{array}$$

   (2.1) Prove que $3$$3$ é recorrente verificando $\mathbb{P}(T_3>n\mid X_0=3)\le (0.9{)}^n\to 0$$\mathbb{P} (T_3 > n \mid X_0=3) \leq (0.9)^n \to 0$ quando $n\to \mathrm{\infty }$$n \to \infty$. (2.2) Prove que $3$$3$ é recorrente não-nulo mostrando que $\mathbb{E}[T_3\mid X_0=3]\le 10$$\mathbb {E}[T_3\mid X_0=3] \leq 10$.

3. Suponha que $\mathbb{P}(T_j\le k\mid X_0=i)\ge \alpha >0,$$\mathbb{P}(T_j \leq k \mid X_0=i) \geq \alpha > 0,$ para todo $i\in S$$i \in S$. Prove que

   $$\mathbb{P}(T_j>nk\mid X_0=i)\le (1-\alpha {)}^n.$$

4. Considere a cadeia de Markov com espaço de estados $S=\{1,2,3,4\}$$S = \{1,2,3,4\}$ e matriz de transição

   $$\begin{array}{c}P=\left[\begin{array}{cccc}0& 1& 0& 0\\ \frac{1}{2}& 0& \frac{1}{2}& 0\\ 0& 0& 0& 1\\ 0& \frac{1}{2}& 0& \frac{1}{2}\end{array}\right].\end{array}$$

   (4.1) Determine, para cada estado $i\in S$$i \in S$, se ele é transiente, recorrente não absorvente ou absorvente. (4.2) Identifique as classes de comunicação da cadeia. Quais classes são fechadas? (4.3) Calcule o período de cada estado (período é assunto da semana que vem).

5. O tempo da $k$$k$-ésima visita ao estado $j$$j$ é:

   $$\begin{array}{c}{T}_j^{(k)}=\{\begin{array}{ll}{T}_j,& \text{ se }k=1\\ min\{n>T_j^{(k-1)}:X_n=j\}& \text{ se }k>1.\end{array}\end{array}$$

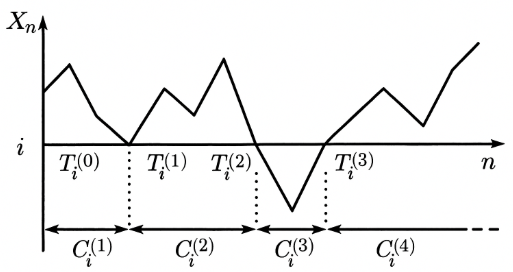
   Os ciclos da cadeia com relação ao estado $j$$j$ são definidos pelos tempos de visita ao estado $j$$j$ por

   $$\begin{array}{c}{C}_j^{(k)}:=\{\begin{array}{ll}{T}_j^{(k)}-T_j^{(k-1)}& \mathbf{\text{ se }}{T}_j^{(k-1)}<\mathrm{\infty }\\ 0& \text{caso sontrário}\end{array}\end{array}$$

   (5.1) Para $k\ge 2$$k\geq 2$, condicionado a $T_j^{(k-1)}<\mathrm{\infty }$$T_j^{(k-1)}<\infty$ é a v.a. $C_j^{(k)}$$C_j^{(k)}$ independente de $\{X_m:m\le T_j^{(k-1)}\}$$\{X_m : m\leq T_j^{(k-1)}\}$ ? (5.2) Mostre que condicionado a $T_j^{(k-1)}<\mathrm{\infty }$$T_j^{(k-1)}<\infty$ o evento $[C_j^{(k)}=n]$$[C_j^{(k)}=n]$ ocorre com probabilidade $\mathbb{P}(T_j=n\mid X_0=j)$$\mathbb P(T_j=n\mid X_0=j)$. (5.3) Use a Lei Forte dos Grandes Números para para mostrar que, com probabilidade 1 vale:

   $$\underset{k\to \mathrm{\infty }}{lim}\frac{T_j^{(k)}}{k}=m_j$$

   onde $m_j$$m_j$ é o tempo médio de recorrência.

6. Prove que $\mathbb{E}[N_j\mid X_0=i]=\frac{f_{ij}}{1-f_{jj}}$$\mathbb E [ N_j \mid X_0=i] = \frac{f_{ij}}{1-f_{jj}}$​.

7. (opcional) Agora consideremos uma cadeia de Markov $(X_n{)}_{n\ge 0}$$(X_n)_{n \ge 0}$ observada apenas em certos instantes. Suponha que $J$$J$ seja um subconjunto do espaço de estados e que observamos a cadeia apenas quando ela assume valores em $J$$J$. O processo resultante $(Y_m{)}_{m\ge 0}$$(Y_m)_{m \ge 0}$ pode ser obtido formalmente definindo

   $$Y_m:=X_{{\tau }_m},$$

   onde ${\tau }_m$$\tau_m$ denota o instante da $m$$m$-ésima visita da cadeia a $J$$J$

   $${\tau }_0:=min\{n>0:X_n\in J\}e{\tau }_{m+1}:=min\{n>{\tau }_m:X_n\in J\}.$$

   para $m=1,2,\dots$$m = 1, 2, \dots$. Supomos que $\mathbb{P}({\tau }_m<\mathrm{\infty }\mid X_0)=1$$\mathbb{P}(\tau_m < \infty\mid X_0) = 1$ para todo $m$$m$. Prove que a propriedade forte de Markov aplica-se para mostrar que, para $i_0,\dots ,i_{m+1}\in J$$i_0, \dots, i_{m+1} \in J$,

   $$\mathbb{P}(Y_{m+1}=i_{m+1}\mid Y_0=i_0,\dots ,Y_m=i_m)=\mathbb{P}(X_{{\tau }_1}=i_{m+1}\mid X_{{\tau }_0}=i_m)=a_{i_m{i}_{m+1}}$$

   onde $a_{ij}=p_{ik}+\sum _{k\notin J}{p}_{ik}{a}_{kj}$$a_{ij} = p_{ik} + \sum_{k\not\in J}p_{ik}a_{kj}$​. Conclua que o processo $(Y_m)$$(Y_m)$​ é também uma cadeia de Markov, com matriz de transição $(a_{ij})$$(a_{ij})$​ com índices restritos ao subconjunto $J$$J$​.

8. Uma partícula realiza passeio aleatório nos 8 vértices de um cubo. Em cada passo, ela permanece no mesmo vértice com probabilidade $1/4$$1/4$, ou move-se para cada um dos três vértices vizinhos com probabilidade $1/4$$1/4$ cada. Sejam $v$$v$ e $w$$w$ vértices diametralmente opostos; a cadeia parte de $v$$v$. Calcule: (a) o número médio de passos até o primeiro retorno a $v$$v$, (b) o número médio de passos até a primeira visita a $w$$w$, (c) o número médio de visitas a $w$$w$ antes do primeiro retorno a $v$$v$​​.

9. O objetivo deste exercício é deduzir equação de renovação:

   $$p_{ij}^{(n)}=\sum _{k=1}^n{f}_{ij}^{(k)}{p}_{jj}^{(n-k)}.$$

   (9.1) Mostre que

   $$[X_n=j]=\bigcup _{k=1}^n[T_j=k,X_n=j],$$

   e que a união é disjunta. Use a decomposição anterior para escrever

   $$\mathbb{P}(X_n=j\mid X_0=i)=\sum _{k=1}^n\mathbb{P}(T_j=k,X_n=j\mid X_0=i).$$

   (9.2) Condicione na informação de que a cadeia atinge $j$$j$ pela primeira vez no tempo $k$$k$. Mostre que

   $$\mathbb{P}(X_n=j\mid T_j=k,X_k=j,X_0=j)=\mathbb{P}(X_{n-k}=j\mid X_0=j)=p_{jj}^{(n-k)}.$$

   (depois do instante $k$$k$, o processo “recomeça” a partir do estado $j$$j$). (9.3) Separando os fatores. Conclua que

   $$\mathbb{P}(T_j=k,X_n=j\mid X_0=i)=\mathbb{P}(T_j=k\mid X_0=i)\mathbb{P}(X_{n-k}=j\mid X_0=j)=f_{ij}^{(k)}{p}_{jj}^{(n-k)}.$$

   (9.4) Substitua na soma do item (1) e obtenha

   $$p_{ij}^{(n)}=\sum _{k=1}^n{f}_{ij}^{(k)}{p}_{jj}^{(n-k)}.$$

   (9.5) Caso particular. Mostre que, para $i=j$$i=j$, a equação se reduz a

   $$p_{ii}^{(n)}=f_{ii}^{(n)}+\sum _{k=1}^{n-1}{f}_{ii}^{(k)}{p}_{ii}^{(n-k)},$$

   que é a forma clássica da equação de renovação para retornos ao mesmo estado.