Prazer, me chamo Teoria dos Grafos
Este texto foi originalmente publicado no Blog UFABC Divulga Ciência
A cidade de Königsberg ficava na antiga Prússia, hoje chamada de Kaliningrado, na atual Rússia. A cidade era cortada pelo rio Pregel, que dividia o seu curso ao redor de duas ilhas: Kneiphof and Lomse. Existiam 7 pontes ligando as duas partes principais de terra às duas ilhas, como mostrado na figura a seguir.
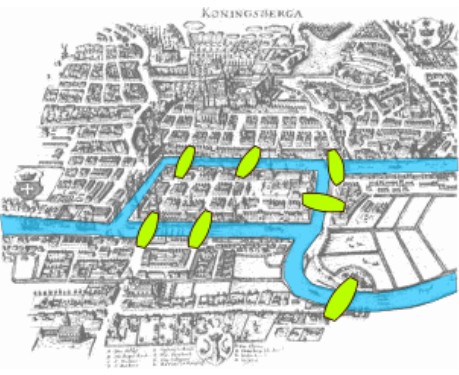

Existe uma lenda que diz que os antigos habitantes de Königsberg tentaram descobrir se era possível percorrer as sete pontes sem repeti-las. De alguma forma, esse problema acabou chegando aos ouvidos do grande matemático e físico suíço Leonhard Euler que, em 1736, o resolveu demonstrando matematicamente que tal feito era impossível. Com esse trabalho nascia a Teoria dos Grafos.
A Teoria dos Grafos é o ramo da matemática que estuda uma estrutura chamada grafo. De forma intuitiva, um grafo é uma coleção de pontos ligados por linhas. Esses pontos são chamados de vértices e as linhas, de arestas. A figura abaixo apresenta dois exemplos de grafos.
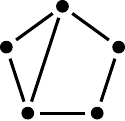
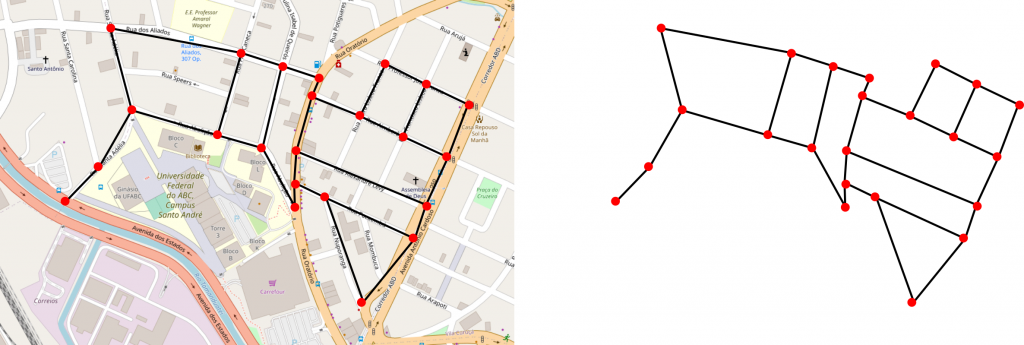
Grafos são úteis para modelar relações par a par entre objetos, o que os tornam uma estrutura adequada para modelar diversas situações práticas. Por exemplo, vértices podem representar cruzamentos de uma cidade e arestas, que há uma rua ligando dois cruzamentos (veja Figura 2). Como outro exemplo, vértices podem representar antenas de telecomunicações e uma aresta ligando dois vértices pode representar pares de antenas que devem operar em frequências distintas, caso contrário causariam interferência entre si. Além disso, não precisamos nos restringir a uma única classe de objetos a ser representa pelos vértices; por exemplo, podemos ter vértices que representam máquinas e outros que representam tarefas. Assim, podemos usar uma aresta ligando um vértice “máquina” a um vértice “tarefa” para representar quais tarefas podem ser executadas em quais máquinas. Para ampliar ainda mais a gama de problemas que podem ser modelados com grafos, podemos associar atributos tais como pesos, cores e direções aos seus vértices e/ou arestas. Por causa disso, diversos problemas práticos importantes, tais como roteamento de veículos, alocação de tarefas, projeto de layout de circuitos e sequenciamento de tarefas, podem ser modelados como problemas em grafos.
Essa riqueza de aplicações faz de grafos uma importante estrutura de dados para a Computação. Por ser uma estrutura tão útil, é importante descobrir quais leis governam essa estrutura, que podem então ser exploradas por “computeiros” no desenvolvimento de algoritmos eficientes para solucionar problemas do mundo real.
Mas o que seriam essas leis? Vejamos… Uma dessas leis diz que todo grafo suficientemente grande possui ao menos dois vértices que têm o mesmo número de arestas tocando neles (aqui, suficientemente grande significa ter pelo menos dois vértices). Por exemplo, no grafo da figura abaixo, cujos vértices foram rotulados para podermos referenciá-los, vemos que existem 2 arestas tocando cada um dos vértices \(v_1\) e \(v_3\).
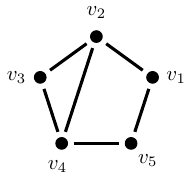
Se olharmos para os grafos exibidos anteriormente, sempre encontraremos um par de vértices que possui exatamente o mesmo número de arestas tocando-os. Meu caro leitor, aqui eu o convido a rabiscar alguns grafos no papel para conferir que tal par de vértices sempre aparece. Não importa o quão exótico e mirabolante seja o grafo que você desenhar, esse par de vértices sempre irá aparecer. Isso é LEI!
Agora, deixe-me ilustrar uma outra lei que sabemos ser respeitada pelos grafos. Mas antes de apresentá-la, eu preciso deixar claro que o que diferencia um grafo de outro é a sua estrutura de conexões. Isso quer dizer que um mesmo grafo pode ser desenhado de diversas formas distintas. Por exemplo, a figura abaixo apresenta dois desenhos do mesmo grafo. A rotulação dos vértices nos ajuda a perceber que os dois desenhos apresentam a mesma estrutura de conexões. Por exemplo, perceba que em ambos os desenhos temos um aresta ligando os vértices \(x_0)\) e \(x_1\) e que em ambos os desenhos não temos uma aresta ligando os vértices \(x_0\) e \(y_1\). E essa coerência com relação ao respeito das conexões em ambos os desenhos não vale somente para esses pares de vértices, elas são válidas para todos os pares de vértices do grafo. Portanto, esses são de fato desenhos do mesmo grafo.
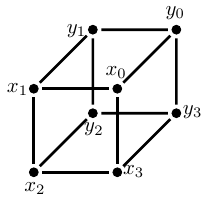
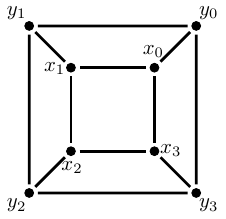
Em algumas aplicações é interessante encontrar um desenho do grafo no qual não há cruzamento de arestas, isto é, em que as arestas só se encontrem nos vértices, como no desenho à direita na figura acima. Sabemos que nem todo grafo pode ser desenhado dessa forma, por exemplo, os dois grafos da figura abaixo. O grafo da esquerda é chamado de \(K_{3,3}\) e o da direita de \(K_5\).
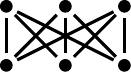
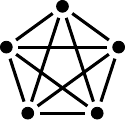
Grafos que podem ser desenhados sem cruzamento de arestas são chamados de grafos planares. Uma pergunta natural é: o que faz um grafo ser planar ou não? E é sobre isso que se trata a segunda lei que vamos mencionar, e que foi provada matematicamente em 1930 por Kuratowski. Essa lei nos diz que todo grafo que não pode ser desenhado sem cruzamento de arestas tem uma espécie de \(K_{3,3}\) ou \(K_5\) “dentro dele”. Isso quer dizer que as únicas estruturas de conexões que impedem um grafo de ser desenhado sem cruzamento de arestas são aquelas apresentadas na figura acima. Isso não é fantástico? Surpreendente?! Pense, de toda uma gama de conexões possíveis, apenas duas delas são responsáveis por impossibilitar que um grafo seja desenhado sem cruzamentos de arestas!
Agora, deixe-me dar uma palavrinha sobre como a pesquisa em teoria dos grafos é desenvolvida. Quando nós sabemos que uma lei é válida, isto é, que essa lei foi demonstrada verdadeira matematicamente, chamamos essa lei de teorema. A todo momento, pesquisadores estão descobrindo novas leis respeitadas pelos grafos, ou seja, novos teoremas. Às vezes, um pesquisador imagina que descobriu uma nova lei, mas ele não é capaz de argumentar logicamente o porquê da propriedade ser válida, isto é, de demonstrá-la matematicamente. Neste caso, o pesquisador anuncia essa possível lei à comunidade científica, que começa a trabalhar para verificar a veracidade ou falsidade dessa nova lei. Essa proposta de lei que ainda não foi confirmada é chamada de conjectura.
Para encerrar a nossa discussão, eu vou mencionar duas conjecturas em Teoria dos Grafos, isto é, duas possíveis leis cuja veracidade das afirmações é desconhecida até os dias atuais. Mas antes de enunciar essas conjecturas eu preciso explicar o que é um ciclo em um grafo. Um ciclo é um percurso fechado que não repete vértices dentro de um grafo. A figura abaixo ilustra um grafo no qual um ciclo foi destacado em vermelho.
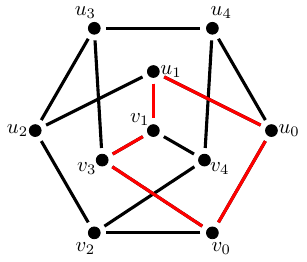
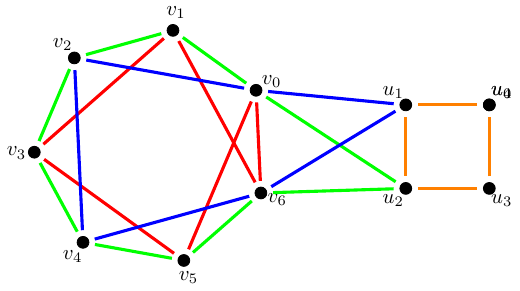
Dizemos que um grafo é par se todo vértice tem um número par de arestas incidentes a ele. Em 1968, Hajós conjecturou uma nova lei para grafos pares. Aqui cabe notar que Hajós não propôs uma lei para qualquer grafo, ele propôs uma lei que é válida apenas para grafos pares. Isso é muito comum em Teoria do Grafos. Quando categorizamos os grafos em algumas famílias levando em conta algum critério estrutural, como o caso dos grafos pares, geralmente conseguimos compreender melhor a estrutura de conexão dos membros de uma dada família e, com isso, conseguimos elencar leis que são válidas exclusivamente para esses membros. Esse é o caso da conjectura feita por Hajós que disse que qualquer grafo par com \(n\) vértices pode ter suas arestas coloridas usando-se no máximo \(\frac{n}{2}\) cores de forma que cada cor forme um ciclo. A figura abaixo ilustra um exemplo de um grafo par que respeita a lei proposta por Hajós. Note que esse grafo tem \(n = 11\) vértices. Pela lei proposta por Hajós, deveria ser possível colorir as arestas desse grafo usando no máximo \(5\) cores (\(\frac{11}{2} = 5,5\) e arredondamos para baixo) de forma que cada cor seja um ciclo. Como podemos ver pelas cores usadas na figura abaixo, tal coloração de fato é possível e, portanto, a conjectura proposta por Hajós é verdadeira para esse grafo.
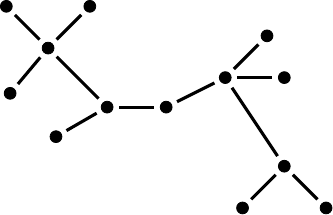
A segunda conjectura que eu gostaria de enunciar diz respeito a grafos que são árvores. Dizemos que um grafo é uma árvore se ele não possui ciclos. A figura abaixo ilustra um exemplo de um grafo que é uma árvore.
Para definirmos essa nova conjectura também precisamos do conceito de rotulação e rotulação graciosa. Uma rotulação é uma atribuição de números inteiros não negativos aos vértices de um grafo, em outras palavras, cada vértice recebe um rótulo que é um número inteiro não negativo. Uma rotulação graciosa de um grafo com \(m\) arestas é uma rotulação tal que, se fizermos a diferença absoluta dos dois rótulos dos vértices de cada aresta do grafo, obtemos os números da sequência \(1, 2, \ldots, m\).
A figura abaixo apresenta um exemplo de rotulação graciosa. O rótulo de cada vértice aparece inscrito dentro dele. Os números em vermelho próximos às arestas são obtidos pela diferença absoluta dos rótulos dos vértices de cada aresta. Por exemplo, note que a aresta com número \(4\) possui vértices com rótulos \(1\) e \(5\), e, de fato, \(|5 – 1| = 4\). Agora olhando apenas os números em vermelho, perceba que eles são os números da sequência \(1, 2, 3, 4\), que é a sequência desejada, uma vez que \(m = 4\). Portanto, a rotulação apresentada para o grafo do exemplo é uma rotulação graciosa.
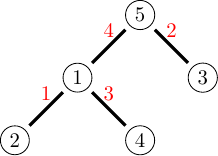
Um grafo para o qual existe uma rotulação graciosa é chamado de gracioso. Rosa, em 1967, conjecturou que toda árvore é graciosa, ou seja, que sempre existe uma rotulação graciosa para um grafo que é uma árvore.
Como vocês podem ter percebido, essas conjecturas estão sem respostas há muitos anos, mas nem todas são assim. A todo ano novas e novas leis em potencial (conjecturas) são propostas. Minha escolha por essas duas se deu principalmente pela simplicidade de enunciá-las e por suas relevâncias. Antes de encerrar, gostaria de mencionar que uma forma de lidar com esses problemas muito difíceis e antigos é verificar que a lei é válida para um grupo menor de grafos. Por exemplo, não sabemos se a conjectura de Hajós é valida para todos os grafos pares, mas sabemos que ela é válida para todos os grafos pares que são planares. Esse tipo de abordagem nos permite ir ganhando terreno aos poucos enquanto vamos compreendendo melhor a estrutura do problema.