Revisão de Álgebra Linear (1) – Operações vetoriais de 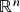 , (sub)espaços vetoriais
, (sub)espaços vetoriais
Para podermos lidar com campos vetoriais, é necessário poder manipulá-los algebricamente. Para tal, precisamos coletar as ferramentas para essa finalidade, fornecidas pela Álgebra Linear.
Operações vetoriais de 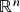 , axiomas de espaço vetorial
, axiomas de espaço vetorial
Lembremos que ![]() pode ser entendido como o conjunto das listas ordenadas de
pode ser entendido como o conjunto das listas ordenadas de ![]() números reais
números reais ![]() :
:
![Rendered by QuickLaTeX.com \[\begin{split} \vx &=(x_1,\ldots,x_n) \\ \Then x_j &=j\text{\emph{-\'{e}sima componente de} }\vx\ ,\\ &\phantom{=}j=1,\ldots,n\ .\end{split}\]](https://pedroribeiro.prof.ufabc.edu.br/wp-content/ql-cache/quicklatex.com-67961b2107b59222d0e398ff1c52a084_l3.png)
Por “ordenadas” entende-se que trocando duas componentes de ![]() de lugar muda a lista, a menos que tais componentes sejam iguais. Os elementos de
de lugar muda a lista, a menos que tais componentes sejam iguais. Os elementos de ![]() são denominados vetores em
são denominados vetores em ![]() ou vetores
ou vetores ![]() -dimensionais.
-dimensionais.
![]() é munido de duas operações vetoriais:
é munido de duas operações vetoriais:
- A soma (vetorial) de dois vetores
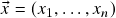 ,
, 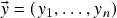 , dada por
, dada por ![Rendered by QuickLaTeX.com \[\begin{split}\vx+\vy &=(x_1+y_1,\ldots,x_n+y_n) \\ \Then x_j+y_j &=j\text{-\'{e}sima componente de }\vx+\vy\ ,\\ &\phantom{=}j=1,\ldots,n\ .\end{split}\]](https://pedroribeiro.prof.ufabc.edu.br/wp-content/ql-cache/quicklatex.com-ae7dfdcd0fca97d8968af7a3c3e3416c_l3.png)
- A multiplicação (pelo) escalar
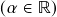 do vetor
do vetor 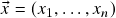 , dada por
, dada por ![Rendered by QuickLaTeX.com \[\begin{split} \alpha\vx &=(\alpha x_1,\ldots,\alpha x_n) \\ \Then \alpha x_j &=j\text{-\'{e}sima componente de }\alpha\vx\ ,\\ &\phantom{=}j=1,\ldots,n\ . \end{split}\]](https://pedroribeiro.prof.ufabc.edu.br/wp-content/ql-cache/quicklatex.com-79453152422b2b9638faa80fc20386d0_l3.png)
As operações vetoriais de ![]() satisfazem a seguinte lista de propriedades, chamadas axiomas de espaço vetorial real ou sobre
satisfazem a seguinte lista de propriedades, chamadas axiomas de espaço vetorial real ou sobre ![]() (em referência ao corpo de escalares
(em referência ao corpo de escalares ![]() , que é o conjunto dos números pelos quais podemos multiplicar vetores, chamados escalares. Não consideraremos outros corpos de escalares além de
, que é o conjunto dos números pelos quais podemos multiplicar vetores, chamados escalares. Não consideraremos outros corpos de escalares além de ![]() ). No que se segue,
). No que se segue, ![]() são vetores quaisquer e
são vetores quaisquer e ![]() são escalares quaisquer quando não especificados.
são escalares quaisquer quando não especificados.
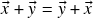 (comutatividade da soma);
(comutatividade da soma);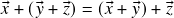 (associatividade da soma);
(associatividade da soma);- Existe um vetor
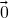 em
em 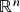 tal que
tal que 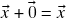 para todo vetor
para todo vetor 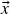 em
em 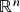 (existência de elemento neutro para a soma). A saber,
(existência de elemento neutro para a soma). A saber,
i.e. todas as componentes de![Rendered by QuickLaTeX.com \[\og=(0,\ldots,0)\ ,\]](https://pedroribeiro.prof.ufabc.edu.br/wp-content/ql-cache/quicklatex.com-d47e962b9d6a65caa90fce7cc7f7d3c4_l3.png)
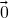 são iguais a zero;
são iguais a zero; - Dado um vetor
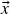 em
em 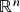 , existe um vetor
, existe um vetor 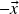 em
em 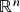 tal que
tal que 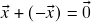 (existência de inverso para a soma). A saber,
(existência de inverso para a soma). A saber,
i.e. a![Rendered by QuickLaTeX.com \[-\vx=(-x_1,\ldots,-x_n)\ ,\]](https://pedroribeiro.prof.ufabc.edu.br/wp-content/ql-cache/quicklatex.com-570b82f68627473d9869295eca2affd1_l3.png)
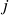 -ésima componente de
-ésima componente de 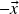 é igual a
é igual a 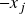 para todo
para todo 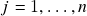 ;
; 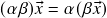 (associatividade da multiplicação escalar);
(associatividade da multiplicação escalar);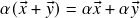 (distributividade da multiplicação escalar com respeito à soma vetorial);
(distributividade da multiplicação escalar com respeito à soma vetorial);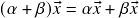 (distributividade da multiplicação escalar com respeito à soma escalar);
(distributividade da multiplicação escalar com respeito à soma escalar);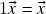 (elemento neutro para a multiplicação escalar).
(elemento neutro para a multiplicação escalar).
Exercício 1. Verifique os axiomas (a)-(h) para as operações vetoriais de
.
Exercício 2. Verifique que
é o único elemento neutro para a soma vetorial de
e que, para todo vetor
,
é o único inverso de
para a soma vetorial de
.
Alternativamente, os Exercícios 1 e 2 serão resolvidos num contexto mais geral mais adiante.
(Sub)espaços vetoriais
Definição 1. Um conjunto
munido de operações vetoriais de soma (vetorial)
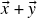
e multiplicação escalar
(
,
) satisfazendo os axiomas (a)–(h) enumerados acima é chamado de espaço vetorial (real ou sobre (o corpo de escalares)
). Neste caso, os elementos de
são chamados de vetores em
.
Propriedades das operações vetoriais que dependem apenas dos axiomas de espaço vetorial (identidades que seguem de um axioma específico dentre os axiomas (a)-(h) terão o axioma usado indicado sobre o sinal de igualdade quando necessário) valem para todos os espaços vetoriais, não apenas ![]() ! Em particular, tais propriedades não dependem das características específicas de
! Em particular, tais propriedades não dependem das características específicas de ![]() e sua operações vetoriais. Por exemplo:
e sua operações vetoriais. Por exemplo:
- Só existe um elemento neutro – portanto, justificadamente denotado por
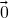 – para a soma vetorial de
– para a soma vetorial de 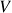 . (de fato, dados vetores
. (de fato, dados vetores 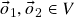 tais que
tais que
para todo vetor![Rendered by QuickLaTeX.com \[\vx+\vo_1=\vx+\vo_2=\vx\]](https://pedroribeiro.prof.ufabc.edu.br/wp-content/ql-cache/quicklatex.com-a1cf4d7e0dac1f962db6cb87e4e5aa55_l3.png)
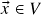 , tomando
, tomando 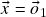 obtemos
obtemos
e tomando![Rendered by QuickLaTeX.com \[\vo_1+\vo_2=\vo_1\]](https://pedroribeiro.prof.ufabc.edu.br/wp-content/ql-cache/quicklatex.com-6615eaf7ae63a10b199b7555d967caa6_l3.png)
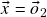 obtemos
obtemos
Concluímos daí e do axioma (a) que![Rendered by QuickLaTeX.com \[\vo_2+\vo_1=\vo_2\ .\]](https://pedroribeiro.prof.ufabc.edu.br/wp-content/ql-cache/quicklatex.com-f89d0a5fabf938ca2b1471c6e5f2ae9d_l3.png)
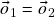 )
) - Dado
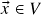 , só existe um inverso de
, só existe um inverso de 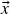 para a soma vetorial de
para a soma vetorial de 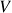 – portanto, justificadamente denotado por
– portanto, justificadamente denotado por 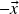 (notação:
(notação: 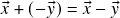 ). Em particular,
). Em particular, 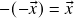 . (de fato, dado
. (de fato, dado 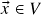 sejam vetores
sejam vetores 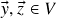 tais que
tais que 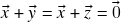 . Somando-se
. Somando-se 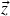 à primeira e última fórmulas, segue que
à primeira e última fórmulas, segue que
e![Rendered by QuickLaTeX.com \[\vz+(\vx+\vy)=\vz+\og\stackrel{(c)}{=}\vz\]](https://pedroribeiro.prof.ufabc.edu.br/wp-content/ql-cache/quicklatex.com-aa4aef389a2f9cd039bc63209fab0e62_l3.png)
de onde concluímos que![Rendered by QuickLaTeX.com \[\vz+(\vx+\vy)\stackrel{(b)}{=}(\vz+\vx)+\vy\stackrel{(a)}{=}(\vx+\vz)+\vy=\og+\vy\stackrel{(c)}{=}\vy\ ,\]](https://pedroribeiro.prof.ufabc.edu.br/wp-content/ql-cache/quicklatex.com-69a5f1dc595bc1590ac5bf99102a9653_l3.png)
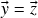 . A última identidade segue disso e de (a))
. A última identidade segue disso e de (a)) 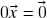 . (de fato,
. (de fato,
Somando![Rendered by QuickLaTeX.com \[0\vx+0\vx\stackrel{(g)}{=}(0+0)\vx=0\vx\ .\]](https://pedroribeiro.prof.ufabc.edu.br/wp-content/ql-cache/quicklatex.com-e40a68aa629963c36c9a0fa91fbb50b9_l3.png)
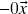 à primeira e última fórmulas, concluímos que
à primeira e última fórmulas, concluímos que
e![Rendered by QuickLaTeX.com \[(0\vx+0\vx)-0\vx\stackrel{(b)}{=}0\vx+(0\vx-0\vx)\stackrel{(d)}{=}0\vx+\og\stackrel{(c)}{=}0\vx\]](https://pedroribeiro.prof.ufabc.edu.br/wp-content/ql-cache/quicklatex.com-3d3e43318fb433d0bd033f4d7c6aaade_l3.png)
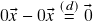 , logo
, logo 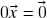 )
)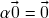 . (de fato,
. (de fato,
De maneira análoga à prova da propriedade anterior, somando-se![Rendered by QuickLaTeX.com \[\alpha\og+\alpha\og\stackrel{(f)}{=}\alpha(\og+\og)\stackrel{(c)}{=}\alpha\og\ .\]](https://pedroribeiro.prof.ufabc.edu.br/wp-content/ql-cache/quicklatex.com-bddfdefbb1f8146150142c3d4e8ef243_l3.png)
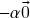 à primeira e última fórmulas, concluímos que
à primeira e última fórmulas, concluímos que
e![Rendered by QuickLaTeX.com \[(\alpha\og+\alpha\og)-\alpha\og\stackrel{(b)}{=}\alpha\og+(\alpha\og-\alpha\og)\stackrel{(d)}{=}\alpha\og+\og\stackrel{(c)}{=}\alpha\og\]](https://pedroribeiro.prof.ufabc.edu.br/wp-content/ql-cache/quicklatex.com-ad3e8f28a3b470b4898f6b540bfe9f78_l3.png)
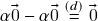 , logo
, logo 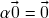 )
)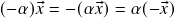 . Em particular,
. Em particular, 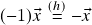 . (de fato,
. (de fato,
e![Rendered by QuickLaTeX.com \[(-\alpha)\vx+\alpha\vx\stackrel{(g)}{=}(-\alpha+\alpha)\vx=0\vx=\og\]](https://pedroribeiro.prof.ufabc.edu.br/wp-content/ql-cache/quicklatex.com-234b346058e0953575ab24f11f7b0629_l3.png)
O resultado desejado segue da unicidade do inverso para a soma vetorial de![Rendered by QuickLaTeX.com \[\alpha(-\vx)+\alpha\vx\stackrel{(f)}{=}\alpha(\vx-\vx)=\alpha\og=\og\ .\]](https://pedroribeiro.prof.ufabc.edu.br/wp-content/ql-cache/quicklatex.com-35466d599a05a2b1b8780047d5d1b44e_l3.png)
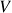 provada acima)
provada acima)- Se
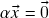 , então
, então 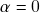 ou
ou 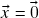 . Em particular, se
. Em particular, se 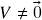 ,
, 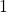 é o único escalar que satisfaz o axioma (h). (de fato, vimos acima que
é o único escalar que satisfaz o axioma (h). (de fato, vimos acima que 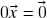 . Se, por outro lado,
. Se, por outro lado, 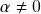 , temos que
, temos que
logo![Rendered by QuickLaTeX.com \[\frac{1}{\alpha}(\alpha\vx)\stackrel{(e)}{=}\left(\frac{\alpha}{\alpha}\right)\vx=1\vx\stackrel{(h)}{=}\vx=\frac{1}{\alpha}\og=\og\ ,\]](https://pedroribeiro.prof.ufabc.edu.br/wp-content/ql-cache/quicklatex.com-ee1494c29835bcf36ee16317a232ab23_l3.png)
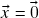 . Para a última afirmação, notar que se
. Para a última afirmação, notar que se 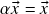 para todo
para todo 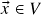 , então
, então
Tomando![Rendered by QuickLaTeX.com \[\alpha\vx-\vx=\alpha\vx+(-1)\vx\stackrel{(g)}{=}(\alpha-1)\vx=\vx-\vx\stackrel{(d)}{=}\og\ .\]](https://pedroribeiro.prof.ufabc.edu.br/wp-content/ql-cache/quicklatex.com-ded3f2aaa39779c5f49cdaf25a2accb7_l3.png)
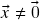 qualquer resulta em
qualquer resulta em 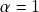 ).
).
Exercício 3. Prove a partir dos axiomas (a)-(h) e/ou de suas consequências provadas acima as seguintes propriedades, válidas para quaisquer vetores
e quaisquer escalares
- Se
e
, então
;
- Se
e
, então
;
;
. Mais em geral,
. (para a definição do símbolo de somatória num espaço vetorial, ver o início da aula 3)
Dentre os exemplos de espaços vetoriais, podemos citar:
- Obviamente,
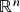 . Em particular,
. Em particular, 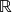
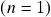 é espaço vetorial sobre si mesmo.
é espaço vetorial sobre si mesmo. - Dado
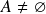 , seja
, seja 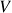 o espaço das funções de
o espaço das funções de 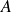 em
em 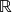 :
:
Definimos em tal![Rendered by QuickLaTeX.com \[ V=F(A,\RR)=\{f:A\To\RR\}\ .\]](https://pedroribeiro.prof.ufabc.edu.br/wp-content/ql-cache/quicklatex.com-edf31d88c261508db4af6904493ff57b_l3.png)
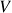 as operações vetoriais pontuais (a seguir,
as operações vetoriais pontuais (a seguir, 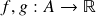 ,
, 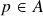 ,
, 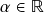 são quaisquer)
são quaisquer)
- Soma (vetorial):
![Rendered by QuickLaTeX.com \[(f+g)(p)=f(p)+g(p)\ ;\]](https://pedroribeiro.prof.ufabc.edu.br/wp-content/ql-cache/quicklatex.com-d8ad4a62870c22419b890d77983605d8_l3.png)
- Multiplicação escalar:
![Rendered by QuickLaTeX.com \[(\alpha f)(p)=\alpha f(p)\ .\]](https://pedroribeiro.prof.ufabc.edu.br/wp-content/ql-cache/quicklatex.com-03fd06c66039cce6202631d0029ca502_l3.png)
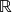 ). De fato, se
). De fato, se 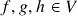 ,
, 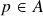 e
e 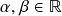 são quaisquer, então:
são quaisquer, então:
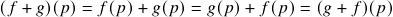 ;
;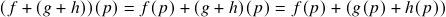
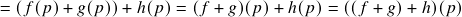 ;
;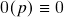 (i.e.
(i.e. 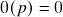 para todo
para todo 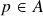 ) satisfaz
) satisfaz 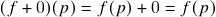 para todo
para todo 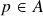 ;
;- Dado
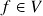 ,
, 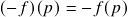
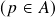 satisfaz
satisfaz 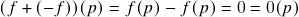 para todo
para todo 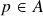 ;
; 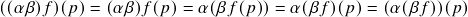 ;
;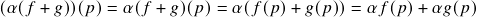
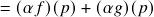 ;
;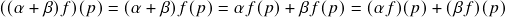
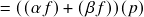 ;
;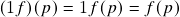 .
.
 ,
, 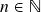 então
então 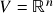 e as operações vetoriais pontuais de
e as operações vetoriais pontuais de 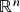 coincidem com as operações vetoriais usuais de
coincidem com as operações vetoriais usuais de 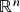 , logo as últimas satisfazem os axiomas (a)-(h), como apontado acima.
, logo as últimas satisfazem os axiomas (a)-(h), como apontado acima. - Soma (vetorial):
- Mais em geral, se
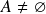 e
e 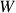 é um espaço vetorial (real), seja
é um espaço vetorial (real), seja 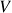 o espaço das funções em
o espaço das funções em 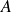 a valores em
a valores em 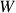 :
:
![Rendered by QuickLaTeX.com \[ V=F(A,W)=\{\vf:A\To W\}\ .\]](https://pedroribeiro.prof.ufabc.edu.br/wp-content/ql-cache/quicklatex.com-55a93db014c6d10348ef201b3af4c674_l3.png)
Definimos em tal
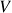 as operações vetoriais pontuais (a seguir,
as operações vetoriais pontuais (a seguir, 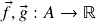 ,
, 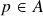 ,
, 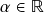 são quaisquer)
são quaisquer)- Soma (vetorial):
![Rendered by QuickLaTeX.com \[(\vf+\vg)(p)=\vf(p)+\vg(p)\ ;\]](https://pedroribeiro.prof.ufabc.edu.br/wp-content/ql-cache/quicklatex.com-f41aaa8756c164612ea7643c5ab8ba7e_l3.png)
- Multiplicação escalar:
![Rendered by QuickLaTeX.com \[(\alpha \vf)(p)=\alpha \vf(p)\ .\]](https://pedroribeiro.prof.ufabc.edu.br/wp-content/ql-cache/quicklatex.com-fe28bebde80c27491a45c25ead6fe3dc_l3.png)
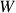 . Os cálculos são exatamente os mesmos.
. Os cálculos são exatamente os mesmos. - Soma (vetorial):
Mais exemplos podem ser obtidos a partir dos dados acima a partir da seguinte
Definição 2. Seja
um espaço vetorial, e
não-vazio. Dizemos que
é subespaço vetorial de
se, dados
e
quaisquer, então
;
.
Se
, dizemos que
é subespaço vetorial próprio de
.
Mostraremos que todo subespaço vetorial ![]() é um espaço vetorial se munido das operações vetoriais herdadas de
é um espaço vetorial se munido das operações vetoriais herdadas de ![]() (o que sempre assumiremos ser o caso). De fato, os axiomas (a), (b) e (e)-(h) são claramente satisfeitos em
(o que sempre assumiremos ser o caso). De fato, os axiomas (a), (b) e (e)-(h) são claramente satisfeitos em ![]() . O que nos resta fazer para obter a validade dos axiomas (c) e (d) em
. O que nos resta fazer para obter a validade dos axiomas (c) e (d) em ![]() é provar, respectivamente, que:
é provar, respectivamente, que:
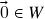 . (se
. (se 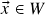 , segue de (ii) que
, segue de (ii) que 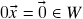 )
)- Se
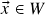 , então
, então 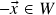 . (se
. (se 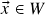 , segue de (ii) que
, segue de (ii) que 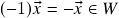 )
)
A vantagem de lidar com subespaços vetoriais é que verificar se ![]() é subespaço vetorial de
é subespaço vetorial de ![]() é bem mais simples do que verificar os axiomas (a)-(h) em
é bem mais simples do que verificar os axiomas (a)-(h) em ![]() . Em particular, ao verificarmos se
. Em particular, ao verificarmos se ![]() , é conveniente verificar se
, é conveniente verificar se ![]() . Se não for o caso, sabemos com certeza que
. Se não for o caso, sabemos com certeza que ![]() não é subespaço vetorial, mesmo se
não é subespaço vetorial, mesmo se ![]() não for vazio.
não for vazio.
(Contra)exemplos de subespaços vetoriais:
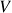 qualquer,
qualquer, 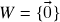 : claramente
: claramente 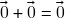 e vimos que
e vimos que 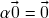 para todo
para todo 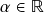 , logo
, logo 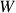 é subespaço vetorial de (V) – o chamado subespaço vetorial trivial de
é subespaço vetorial de (V) – o chamado subespaço vetorial trivial de 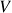 .
.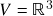 ,
, 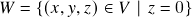 : claramente
: claramente 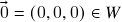 . Além disso, temos que se
. Além disso, temos que se 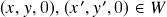 e
e 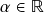 então
então
e![Rendered by QuickLaTeX.com \[(x,y,0)+(x',y',0)=(x+x',y+y',0)\in W\]](https://pedroribeiro.prof.ufabc.edu.br/wp-content/ql-cache/quicklatex.com-c72cd62032e97331f069696e4e240783_l3.png)
![Rendered by QuickLaTeX.com \[ \alpha(x,y,0)=(\alpha x,\alpha y,0)\in W\ .\]](https://pedroribeiro.prof.ufabc.edu.br/wp-content/ql-cache/quicklatex.com-36d0e35a47ced5561eb01c49d76c6695_l3.png)
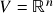 ,
, 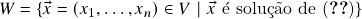 , onde \eqref{ch1e2} é o sistema linear homogêneo
, onde \eqref{ch1e2} é o sistema linear homogêneo (1)
Claramente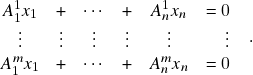
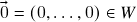 . Além disso, se
. Além disso, se 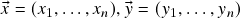 pertencem a
pertencem a 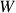 e
e 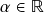 , então
, então
e![Rendered by QuickLaTeX.com \[ \left{\begin{array}{cccccr} A^1_1(x_1+y_1) & + & \cdots & + & A^1_n(x_n+y_n) & =0 \\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ A^m_1(x_1+y_1) & + & \cdots & + & A^m_n(x_n+y_n) & =0 \end{array}\right.\]](https://pedroribeiro.prof.ufabc.edu.br/wp-content/ql-cache/quicklatex.com-49b35920836c9e25fcd32e3b2ffa0313_l3.png)
logo![Rendered by QuickLaTeX.com \[ \left{\begin{array}{cccccr} A^1_1(\alpha x_1) & + & \cdots & + & A^1_n(\alpha x_n) & =0 \\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ A^m_1(\alpha x_1) & + & \cdots & + & A^m_n(\alpha x_n) & =0 \end{array}\right.\ ,\]](https://pedroribeiro.prof.ufabc.edu.br/wp-content/ql-cache/quicklatex.com-d5116a51cd735cc32d8dddf12143154c_l3.png)
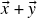 e
e 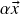 também pertencem a
também pertencem a 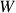 . Veremos mais adiante que esse é um exemplo genérico: todo subespaço vetorial de
. Veremos mais adiante que esse é um exemplo genérico: todo subespaço vetorial de 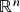 é o espaço de soluções de algum sistema linear homogêneo. Por outro lado, se o lado direito de alguma das equações de (1) não fosse zero (i.e. o sistema passasse a ser não-homogêneo), então
é o espaço de soluções de algum sistema linear homogêneo. Por outro lado, se o lado direito de alguma das equações de (1) não fosse zero (i.e. o sistema passasse a ser não-homogêneo), então 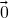 não pertenceria a
não pertenceria a 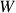 pois nesse caso tal equação obviamente não pode ser satisfeita. Logo, nesse caso
pois nesse caso tal equação obviamente não pode ser satisfeita. Logo, nesse caso 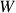 não pode ser subespaço vetorial de
não pode ser subespaço vetorial de 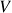 .
.

One Comment