O que é um algoritmo?

• Um conjunto de regras bem definidas que:

  • recebem uma entrada
  • produzem uma saída

• É uma ferramenta para resolver um problema de maneira sistemática:

  • calcular o produto de dois números
  • ordenar um conjunto de itens
  • encontrar o menor caminho entre uma origem e um destino

O que é um algoritmo?

• Consideramos que todo problema possui uma entrada e uma saída bem definidas.

• Dizemos que um algoritmo está correto (ou que ele resolve o problema em questão) se para qualquer caso de entrada do problema, ele produz a saída correta.

• Iremos sempre supor que a entrada recebida por um algoritmo satisfaz as restrições definidas na descrição do problema.

O que é um algoritmo?

• Exemplo: se o problema é ordenar um conjunto de inteiros, um algoritmo estará correto se e somente se for capaz de ordenar qualquer conjunto de inteiros.
  • Se houver algum número real ou imaginário, por exemplo, dentre o conjunto de números, o algoritmo não necessariamente irá ordená-los.

Por que estudar algoritmos?

• Algoritmos (juntamente com estruturas de dados) são muito importantes em praticamente todas as áreas da Ciência da Computação

  • Roteamento, criptografia, computação gráfica, banco de dados, ...

• Permite inovação tecnológica, superando até mesmo o avanço exponencial da lei de Moore.

  • Google PageRank, Projeto Genoma Humano, ...

Por que estudar algoritmos?

• Auxilia com novos pontos de vista em outras áreas.

  • Economia, evolução, mecânica quântica, ...

• Desafiador e divertido.

  • Exige muita criatividade, raciocínio lógico e capacidade analítica

Por que estudar algoritmos?

Suponha que os computadores fossem infinitamente rápidos e que a memória do computador fosse gratuita. Você teria alguma razão para estudar algoritmos? A resposta é sim, se não por outra razão, pelo menos porque você ainda gostaria de demonstrar que o método da sua solução termina, e o faz com a resposta correta.
(Cormen, T. H.; Leiserson, C. E.; Rivest, R. L.; Stein, C.)

O que é análise de algoritmos?

• Objetiva prever o comportamento/desempenho de um algoritmo sem ter que implementá-lo.

• Esse comportamento envolve o uso de recursos como memória, largura de banda e tempo.

• Análise da corretude.

O que é análise de algoritmos?

• Uma vez que descrevemos um algoritmo para um problema, existem três principais perguntas que sempre devemos fazer:

1. O algoritmo está correto?
2. Quantos recursos o algoritmo consome?
3. É possível fazer melhor?

O algoritmo está correto?

• A corretude de um algoritmo pode ser afirmada quando se diz que o algoritmo é correto com respeito à determinada especificação (isto é, para cada entrada ele produz a saída esperada).

  • corretude parcial: se o algoritmo retornar uma resposta, ela deve estar correta
  • corretude total: que requer que o algoritmo tenha um fim

Quantos recursos o algoritmo consome?

• Descrever o comportamento em função do tamanho da entrada, contando o número de passos básicos ou unidades de memória que são consumidos pelo algoritmo.

  • Pior caso
  • Caso médio

É possível fazer melhor?

• Esse algoritmo é a melhor maneira de resolver o problema, ou existem abordagens que consomem menos recursos?

  • É possível encontrar um algoritmo que requer um menor número de passos básicos ou unidades de memória para o problema?
  • Qual é menor quantidade de recursos necessários para resolver um problema, e o quão longe estamos dela?

Exemplo: multiplicação

• Antes de discutir a teoria e ferramentas para responder essas perguntas, vamos ver o exemplo do algoritmo de mutliplicação de dois números que aprendemos no ensino fundamental:
  • multiplicar o multiplicando $(X)$ pelo multiplicador $(Y)$, dígito por dígito, adicionando os resultdos com os deslocamentos adequados

Exemplo: multiplicação

Seja $x=1234$ e $y=5678$, então:

$\def\arraystretch{1} \begin{array}{crrrrrrr} & & & & 5 & 6 & 7 & 8 \\ & & & \times & 1 & 2 & 3 & 4 \\ \hline & & & 2 & 2 & 7& 1& 2 \\ & & 1 & 7 & 0 & 3 & 4 & 0 \\ & 1 & 1 & 3 & 5 & 6 & 0 & 0 \\ \ + & 5 & 6 & 7 & 8 & 0 & 0 & 0 \\ \hline & 7 & 0 & 0 & 6 & 6 & 5 & 2 \end{array}$

Algortimo

• Vamos ver uma implementação dessa ideia em python.
• Só podemos multiplicar dígitos
• Usaremos as funções auxiliares para transformar um número em uma lista de dígitos, e vice-versa

def digitos(x):
    d = [ int(a) for a in str(x) ]
    d.reverse()
    return d

def inteiro(digitos):
    return sum( [ 10**(len(digitos)-i-1)*digitos[i] for i in range(len(digitos))])

Algortimo

Uma possível implementação:

def multiplicaFundamental( X, Y ): # X e Y são inteiros
    x = digitos(X)
    y = digitos(Y)
    parcelas = [] # multiplicação por cada dígito
    for deslocamento,xDigito in enumerate(x):
        parcial = [0 for i in range(deslocamento)]  # 0s de deslocamento
        transporte = 0  
        for yDigito in y:
            produto = digitos( xDigito * yDigito + transporte )
            parcial.insert( 0, produto[0] )
            transporte =  produto[1] if len(produto) > 1 else 0
        parcial.insert(0, transporte)
        parcelas.append(inteiro(parcial))
    return sum(parcelas)

O algoritmo está correto?

• Para qualquer entrada que ele recebe, ele devolve a saída esperada?

• Seja $x=x_{n-1}\dots x_1x_0$, em que $x_i$ é um dígito de de 0 a 9. Note que o algoritmo calcula:
  $\sum_{i=0}^{n-1} y \times x_i \times 10^i$
  o que equivale exatamente a $x\times y$

• Como não fizemos nenhuma suposição sobre $x$, $y$ ou $n$, a análise acima indica que o algoritmo está correto

Quantos recursos o algoritmo consome?

• Vamos considerar o consumo de tempo (podemos modificar ligeiramente o algoritmo para mantar a soma parcial a cada dígito, mantendo o consumo de memória constante).

• Uma ideia inicial seria fazer várias simulações com diferentes valores de $x$ e $y$, e medir o tempo

  • Desvantagens
    • Depende de características do ambiente em que é executado
    • Não permite comparações genéricas com algoritmos que foram testados em outros ambientes
    • Não permite um estudo teórico/analítico sobre o algoritmo

Quantos recursos o algoritmo consome?

• Como mencionado, nos preocupamos com o número de passos básicos realizados
• Note que no algoritmo de multiplicação, para obter o primeiro produto parcial ($y \times x_0$) precisamos de $n$ multiplicações de 1 dígito, e talvez $n-1$ somas para o transporte. Isto é, no máximo $2n$ operações básicas (soma e multiplicação de 1 digito).
• O mesmo raciocínio se aplica para todos os dígitos de $x_i$ de $x$, isto é, no máximo $2n^2$ operações.
• Analogamente, a soma final consome no máximo outras $2n^2$ operações.

Quantos recursos o algoritmo consome?

• Podemos concluir que o algoritmo consome $cn^2$ operações básicas, em que $c$ é uma constante que independe do número de dígitos $n$.
• Dizemos que o algoritmo tem um tempo de execução $O(n^2)$ (veremos com mais detalhes mais adiante no curso)
• PERGUNTA: O que acontece se o tamanho da entrada (o número de dígitos) dobra? E se quadruplica?

Quantos recursos o algoritmo consome?

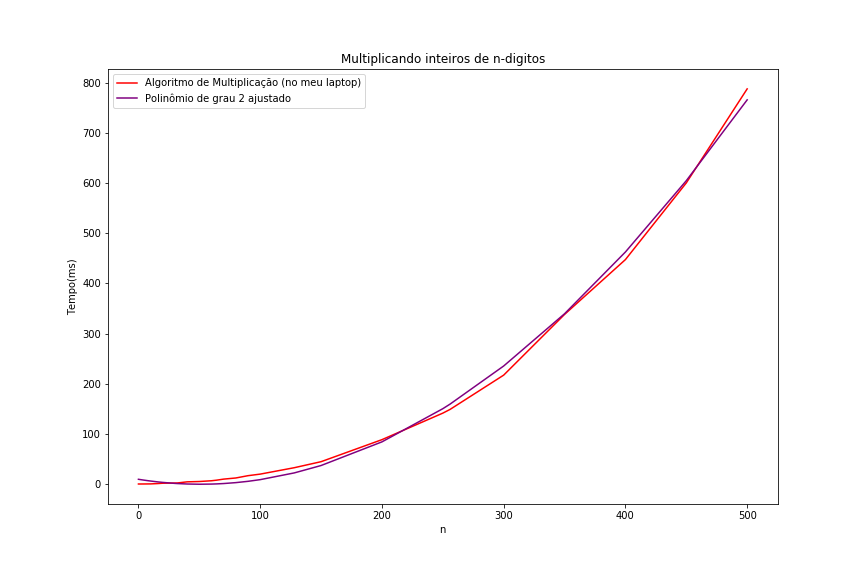
Dá pra fazer melhor ?

• É possível encontrar $x\times y$ com menos do que $cn^2$ operações básicas?

• Até agora, talvez você nunca tenha pensado nisso, mas aresposta é sim!

• Existem algoritmos melhores do que esse que aprendemos no colégio.

Exemplo

Seja $x=1234$ e $y=5678$. Vamos dividir os dígitos desses números tal que $x = \underbrace{12}_{a}\underbrace{34}_{b},y = \underbrace{56}_{c}\underbrace{78}_{b}$

• (1) Calcular $a\cdot c = 672$
• (2) Calcular $b\cdot d = 2652$
• (3) Calcular $(a+b)(c+d) = 134 \cdot 46 = 6164$
• (4) Calcular $(3)-(2)-(1) = 2840$
• Calcular $(1)\cdot 10^4 + (2) + (4)\cdot 10^2 = 6720000 + 2652 +284000 = 7006652 = 1234\cdot 5678$

Exemplo

• Por que funciona?
  • Seja $x = 10^\frac{n}{2}a + b, y = 10^\frac{n}{2}c + d$
  • Então:
    $\begin{aligned} xy &= (10^\frac{n}{2}a + b)(10^\frac{n}{2}c + d) \\ & = 10^n \underbrace{ac}_{(1)}+ 10^\frac{n}{2}\underbrace {(ad + bc)}_{(?)} + \underbrace{db}_{(2)} \end{aligned}$

Exemplo

• Para caucular o termo $(ad + bc)$ mais eficientemente, podemos usar a truque de Gauss:

$(a+b)(c+d) = ac + ad + bc + bd$

$\therefore (ad + bc) = \underbrace{\underbrace{(a+b)(c+d)}_{(3)} - \underbrace{ac}_{(1)} - \underbrace{bd}_{(2)}}_{(4)}$

• Como já teríamos que calcular (2) e (1) de qualquer maneira, reduzimos o número de computações para calcular $(ab+bc)$ calculando (3) e subraindo (2) e (1).

Algoritmo de Karatsuba

• O algoritmo de Karatsuba aplica a idea recursivamente:
  1. Recursivamente calcule $ac$
  2. Recursivamente calcule $bd$
  3. Recursivamente calcule $(a+b)(c+d)$
  4. Cacular e retornar $x\cdot y=10^n \underbrace{ac}_{(1)}+ 10^\frac{n}{2}(\underbrace {(a+b)(c+d)}_{(3)}-\underbrace{ac}_{(1)}-\underbrace{db}_{(2)}) + \underbrace{db}_{(2)}$
• O caso base da recursão é quando os números a multiplicar só tem 1 dígito.
• Requer 3 multiplicações recursivas e algumas adições em cada chamada

Algoritmo de Karatsuba

• O algoritmo de Karatsuba calcula recursivamente
  $\begin{aligned} xy &= (10^\frac{n}{2}a + b)(10^\frac{n}{2}c + d)\\ & = 10^n ac+ 10^\frac{n}{2}(ad + bc) + db \end{aligned}$
• Para um único passo, claramente essa expressão é equivalente a $xy$. - É possível provar por indução em $n$ que o algoritmo está correto (experimente fazer como exercício).

Algoritmo de Karatsuba

• Qual é a complexidade do algoritmo de Karatsuba?
• Verimos isso mais formalmente no decorrer do curso, mas em termos gerais:
  • A cada chamada, dividimos um problema de tamanho $n$ em três poblemas de tamanho $\frac{n}{2}$, até chegar em um problema de tamanho 1.
  • Se dividirmos um número $n$ pela metade $\log_2(n)$ vezes, portanto, o número de níveis $l$ da recursão é $\log_2(n)$
  • No primeiro nível, temos $3$ chamadas. No segundo nível, cada chamada dá origem a outras $3$, portanto $3^2$,..., e no último nível, $3^l$ chamadas.
  • A complexidade é então:
    $O(3^{\log_2(n)})= O(n^{log_2 3})\approx O(n^{1.6})$

Algoritmo de Karatsuba

def digitos(x):
    return [ int(a) for a in str(x) ]

def inteiro(digitos):
    return sum( [ 10**(len(digitos)-i-1)*digitos[i] for i in range(len(digitos))])

def karatsuba( X, Y ):
    return karatsuba_recursivo( digitos(X), digitos(Y))

Algoritmo de Karatsuba

def karatsuba_recursivo( x, y ):  
    n = max( len(x), len(y) )
    # acrescenta zeros se os tamanhos forem diferenes
    while len(x) < n:
      x.insert(0,0)
    while len(y) < n:
      y.insert(0,0)
    if n == 1:
      return x[0]*y[0] # caso básico, multipliação de dois dígitos
    meio = round(n/2)
    a = x[:meio] # [ x[0], x[1], ..., x[meio-1] ]
    b = x[meio:] # [ x[meio], ..., x[n-1] ]
    c = y[:meio]
    d = y[meio:]
    p1 = karatsuba_recursivo( a , c )
    p2 = karatsuba_recursivo( b , d )
    p3 = karatsuba_recursivo( digitos( inteiro(a) + inteiro(b) ) , digitos( inteiro(c) + inteiro(d) ) )
    return  p1 * 10**(2*(n - meio)) + (p3-p2-p1) * 10**(n-meio) + p2

Comparando os dois algoritmos

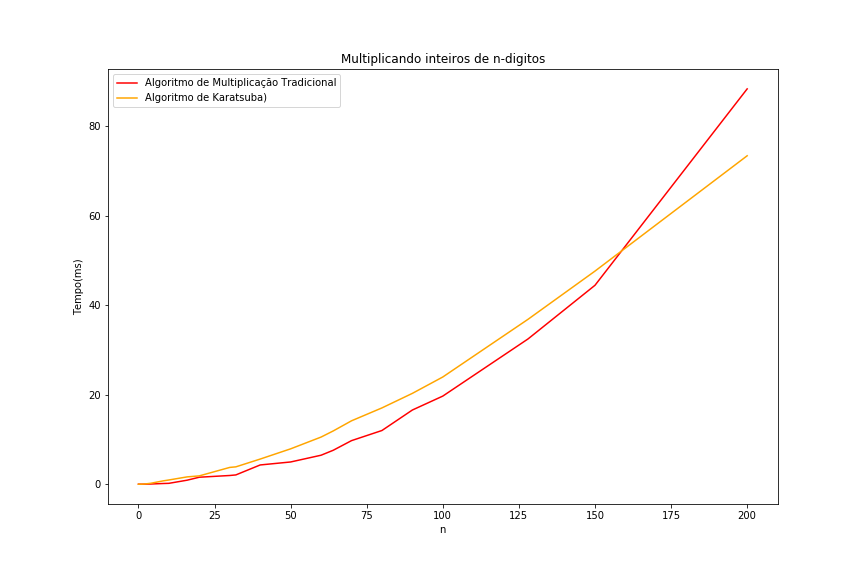
Comparando os dois algoritmos

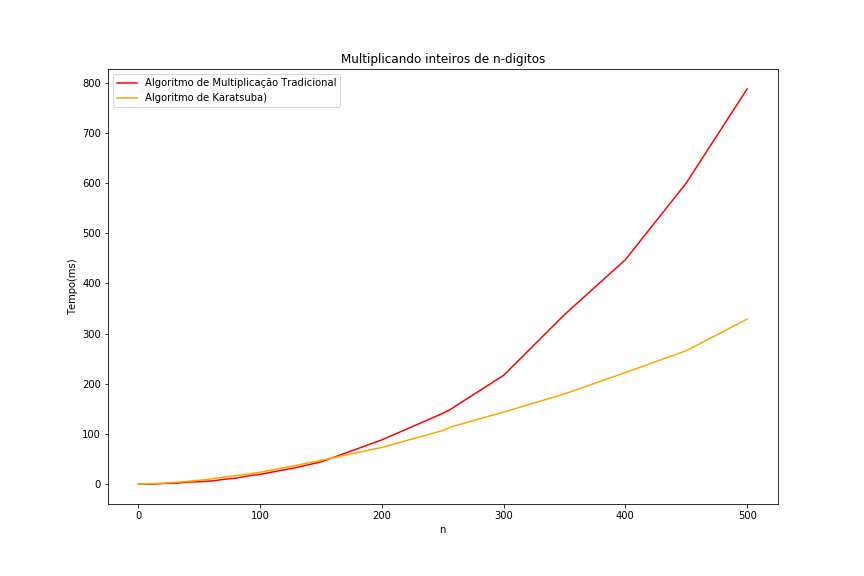
É possível fazer melhor?

• Sim!
  • Toom-Cook(1963) - Ao invés de quebrar em 3 problemas de tamanho $\frac{n}{2}$, quebra em 5 problemas de $\frac{n}{3}$, com tempo de execução $O(n^{1.465})$
  • Schönhage-Strassen (1971) - tempo de execução $O(n\log(n)\log\log(n))$
  • Furer (2007) - tempo de execução $n\log (n) 2^{O(\log(n))}$
  • Harvey-Hoever (2019) - tempo de execução $O(n \log(n))$
• Existem diversos algoritmos para esse problema

É possível fazer melhor?

• Um limite trivial inferior é $O(n)$, pois na melhor das hipóteses temos que percorrer todos os dígitos, mas não se conhece (nem mesmo se sabe se é possível) um algoritmo com esse desempenho.

• Também não se conhece um limite do menor custo possível

Restante do curso

• Vocabulário básico para projeto e análise de algoritmos (notação assintótica).

• Técnicas de projeto de algoritmos (divisão e conquista, algoritmos gulosos, programação dinâmica).

  • Não existem receitas prontas para solução de problemas em geral.

• Uso e análise de estruturas de dados.

  • Uma única estrutura não funciona bem para todos os propósitos.

• Problemas em NP-Completo e o que fazer com eles.

  • Em geral consideramos eficiente um algoritmo que seja rápido e veremos vários problemas para os quais bons algoritmos existem. Mas existem vários problemas para os quais não se conhece solução eficiente.