Árvore de busca em profundidade

• A execução do algoritmo de busca em profundidade gera uma árvore chamada árvore de busca em profundidade.

Árvore de busca em profundidade

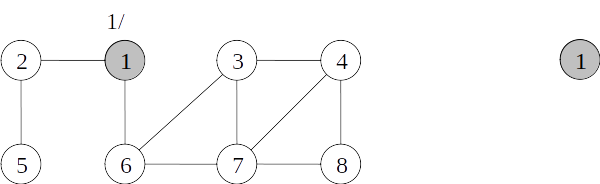
Árvore de busca em profundidade

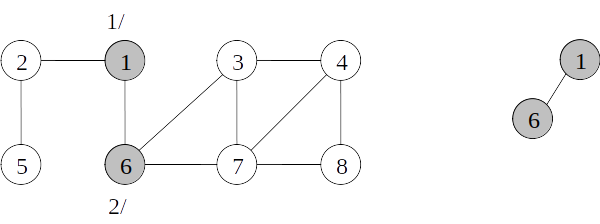
Árvore de busca em profundidade

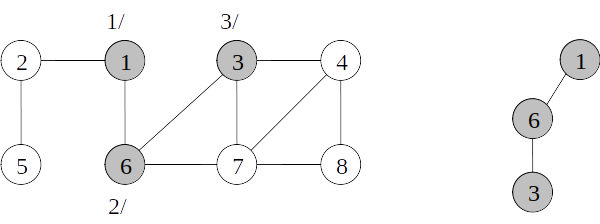
Árvore de busca em profundidade

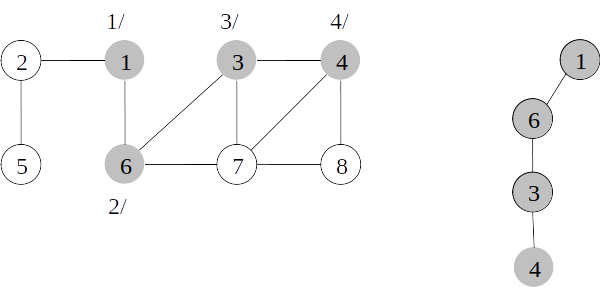
Árvore de busca em profundidade

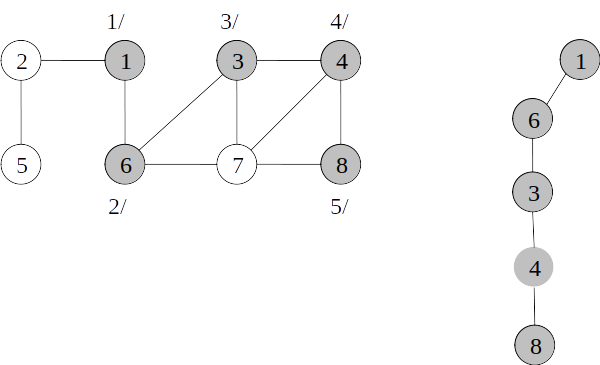
Árvore de busca em profundidade

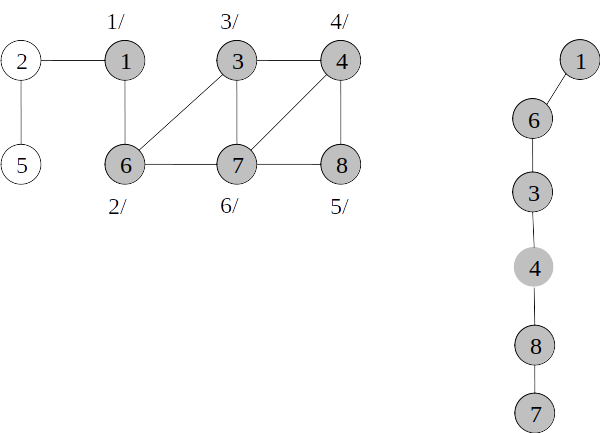
Árvore de busca em profundidade

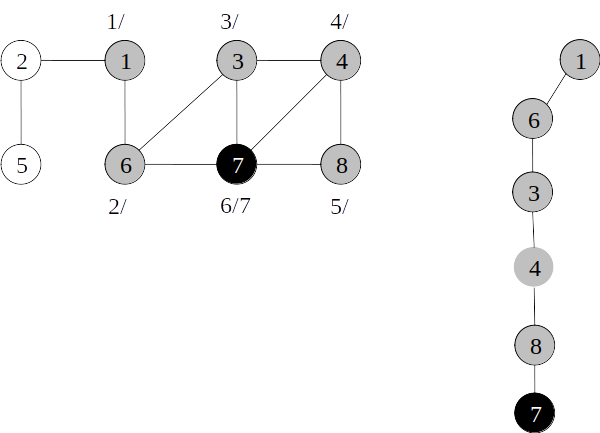
Árvore de busca em profundidade

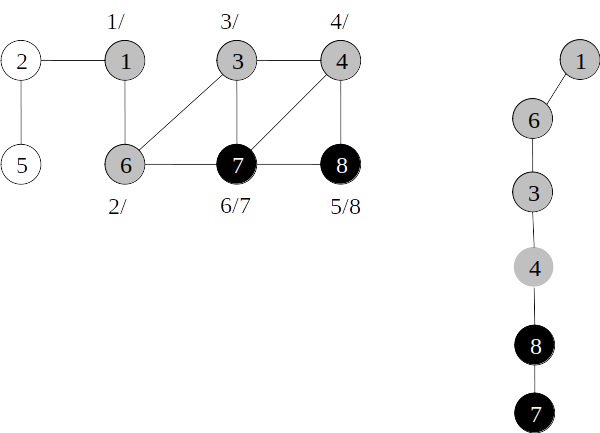
Árvore de busca em profundidade

Árvore de busca em profundidade

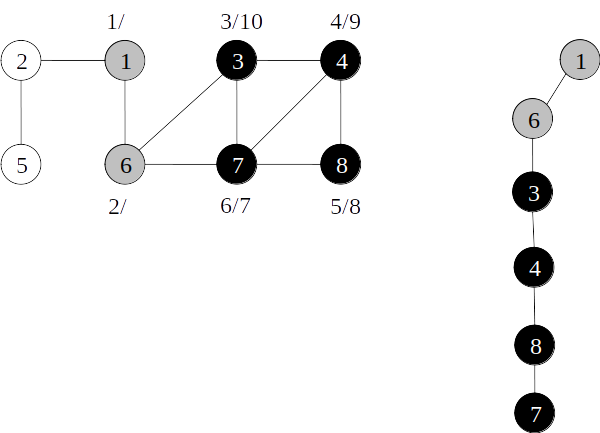
Árvore de busca em profundidade

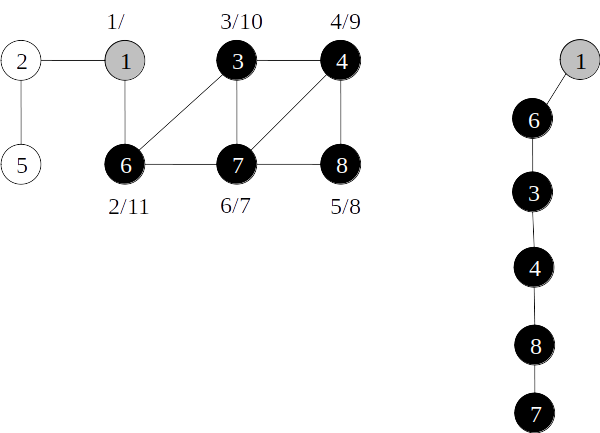
Árvore de busca em profundidade

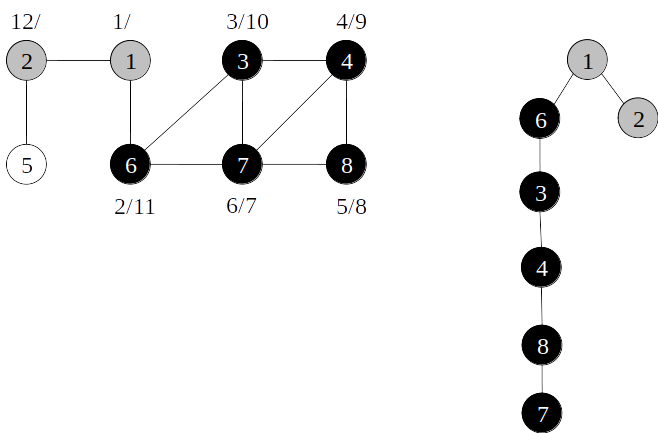
Árvore de busca em profundidade

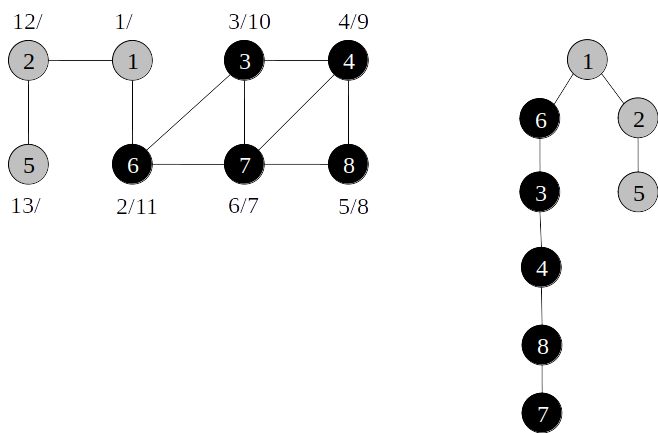
Árvore de busca em profundidade

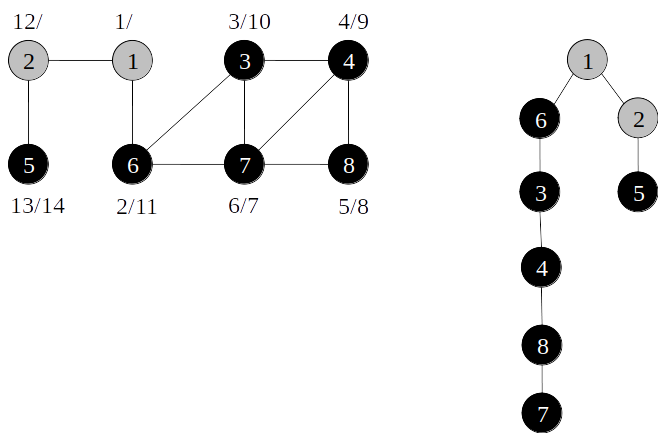
Árvore de busca em profundidade

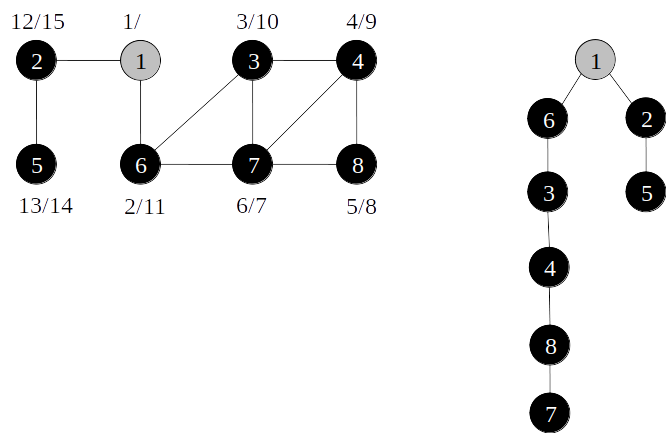
Árvore de busca em profundidade

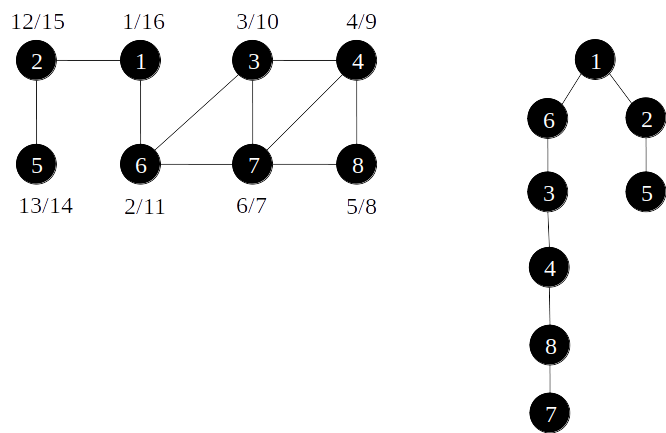
Árvore de busca em largura

• A execução do algoritmo de busca em largura gera uma árvore chamada árvore de busca em largura.

Árvore de busca em largura

Árvore de busca em largura

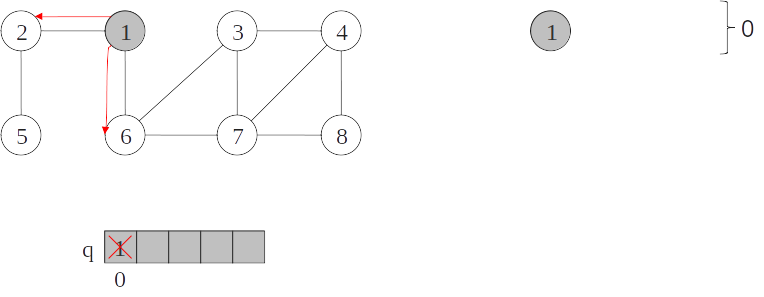
Árvore de busca em largura

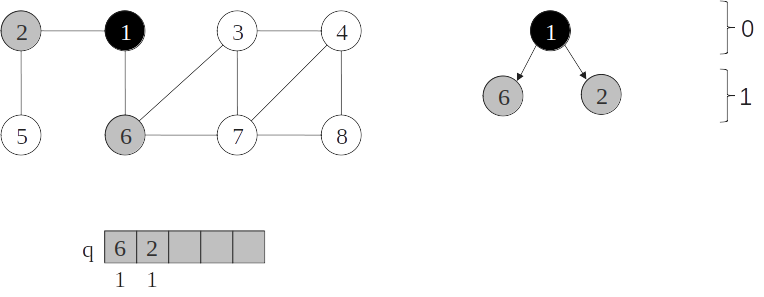
Árvore de busca em largura

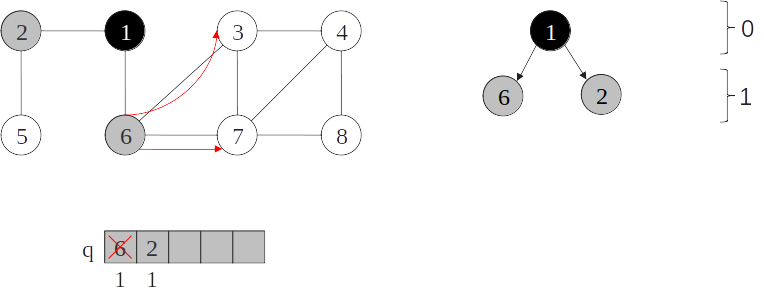
Árvore de busca em largura

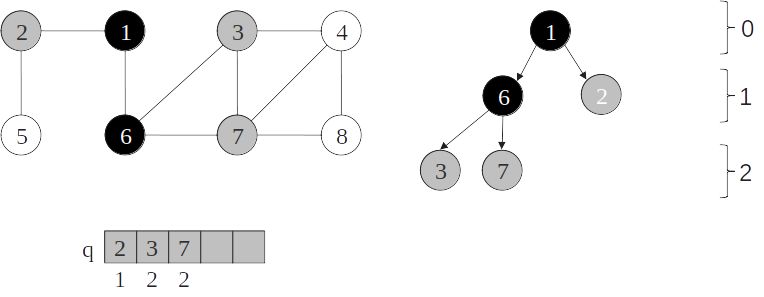
Árvore de busca em largura

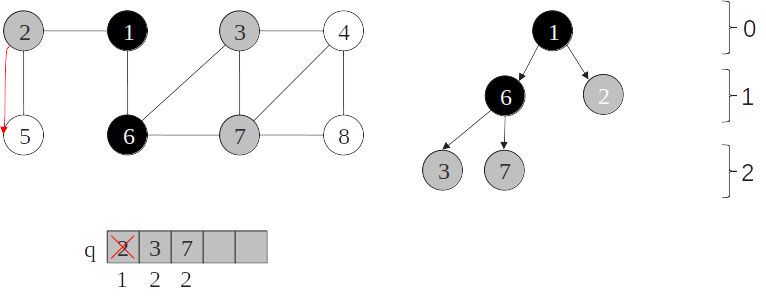
Árvore de busca em largura

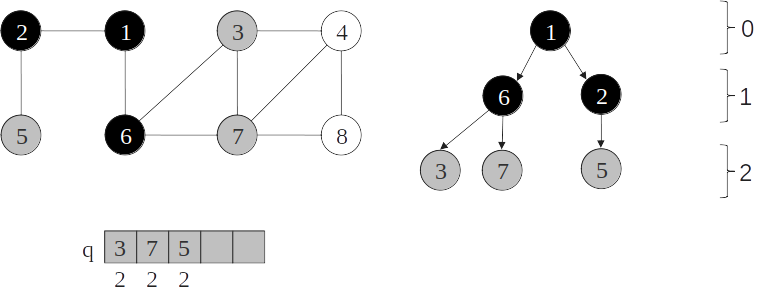
Árvore de busca em largura

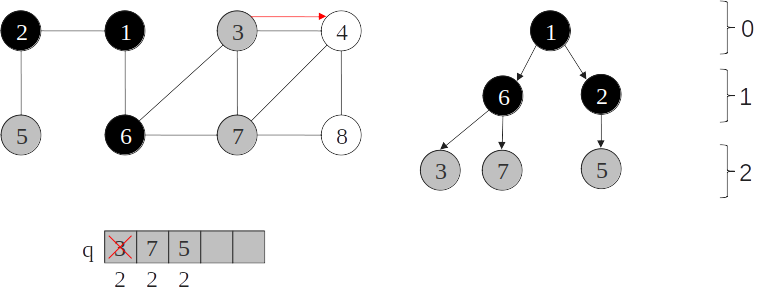
Árvore de busca em largura

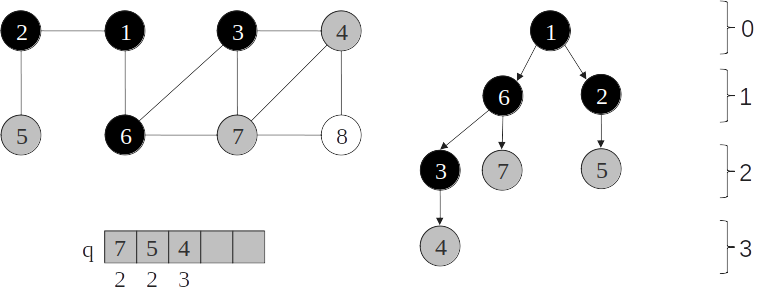
Árvore de busca em largura

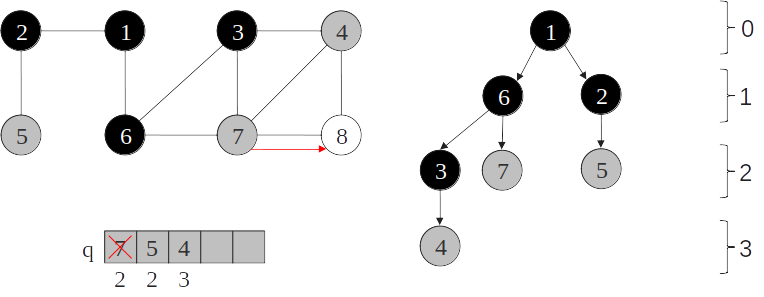
Árvore de busca em largura

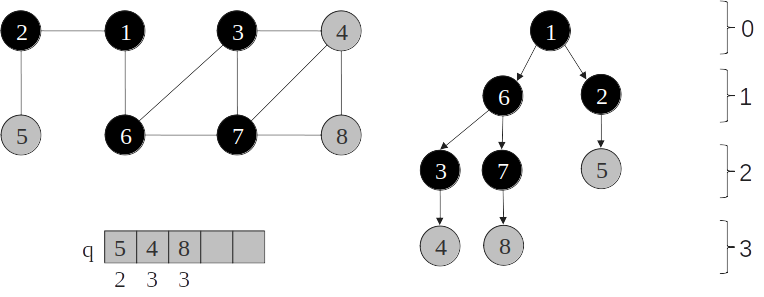
Árvore de busca em largura

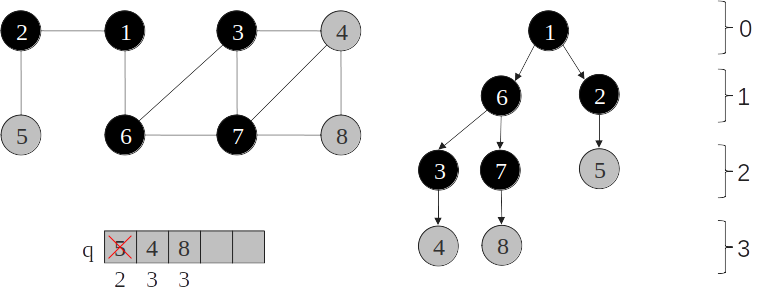
Árvore de busca em largura

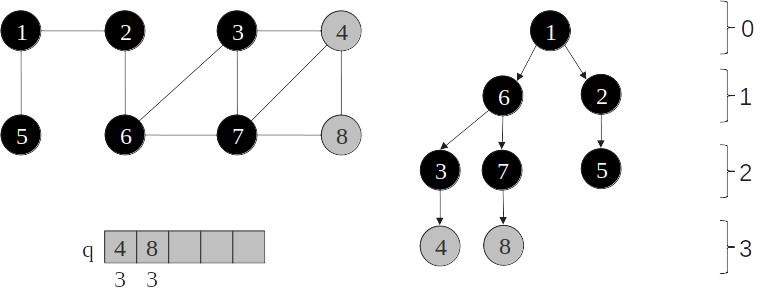
Árvore de busca em largura

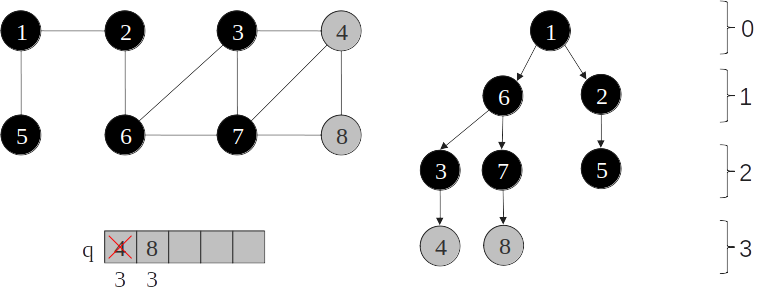
Árvore de busca em largura

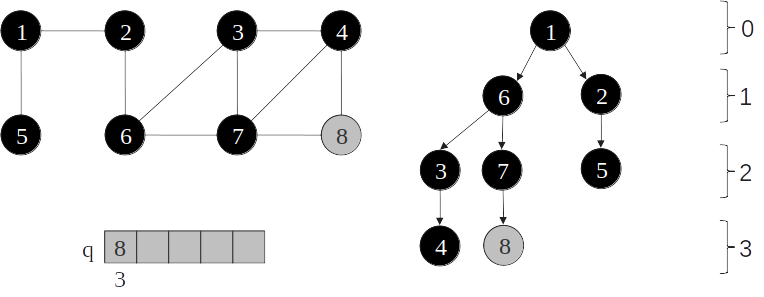
Árvore de busca em largura

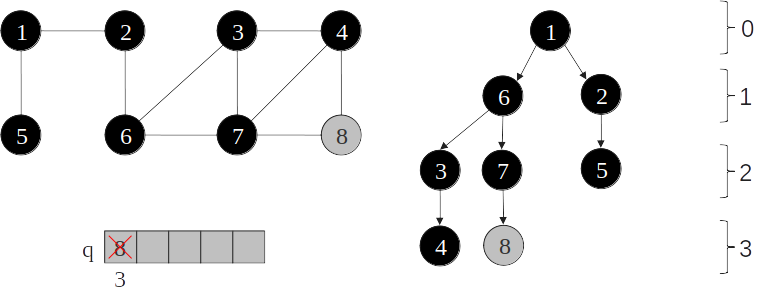
Aplicações de busca em Grafos

• Diversos problemas podem ser resolvidos utilizando a busca em largura ou profundidade (ou adaptações desses algoritmos)
  • Distância entre Vértices
  • Components conexas (em grafos não direcionados)
  • Verificação de Grafos acíclicos
  • Ordenação topológica
  • Componentes fortemente conexas

Menor distância até vértices

• Dado um grafo G, a distância entre dois vértices $u$ e $v$, denotada por $dist_G(u, v)$ é a menor quantidade de arestas de um caminho entre $u$ e $v$.
• Quando não existe caminho entre $u$ e $v$, definimos $dist_G(u, v) = \infty$.
• Ao percorrer o grafo, o algoritmo de busca em largura visita os vértices de acordo com sua distância ao vértice inicial $s$.
• Assim, durante esse processo, uma simples modificação do algoritmo pode facilmente calcular a distância entre $s$ e $v$, para todo vértice $v \in V(G)$
• O algoritmo salva essa distância em um atributo $v$.distancia.

BuscaLarguraDistancia

Buscar Componentes

• Os algoritmos BuscaLargura e BuscaProfundidade visitam todos os vértices que são alcançáveis a partir de $s$, isto é, todos os
  vértices que estão na mesma componente conexa que $s$ está.
• Se o grafo é conexo, então as buscas irão visitar todos os vértices do grafo.
• No entanto, se o grafo não é conexo, existirão ainda vértices não visitados ao fim de uma execução desses dois algoritmos

Buscar Componentes

• Após a execução de um algoritmo de busca a partir de um certo nó, todos os nós daquela componente estão marcados como visitados ("pintados de preto")
• Podemos usar os algoritmos de busca como uma sub-rotina
  • Iterar sobre todos os nós do vértice.
  • Ao encontrar algum nó não visitado, fazemos uma chamada a um dos algoritmos de busca
  • Adicionamos um novo campo $v$.componente a cada nó $v$, correspondente ao primeiro vértice (vértice representante da componente) de uma nova chamada do algoritmo de busca

Buscar Componentes

Buscar Componentes

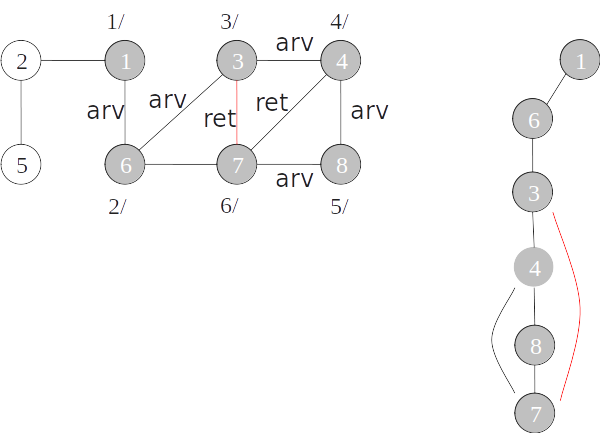
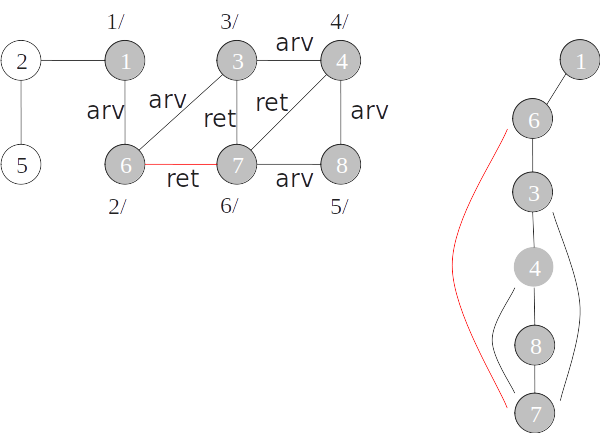
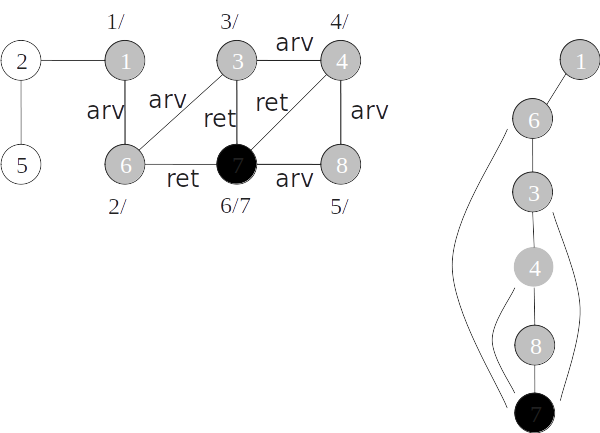
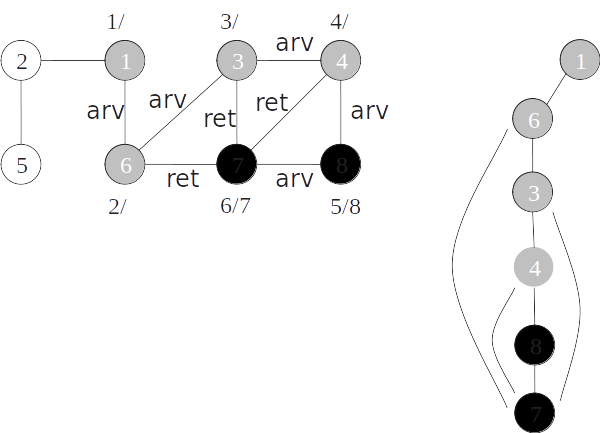
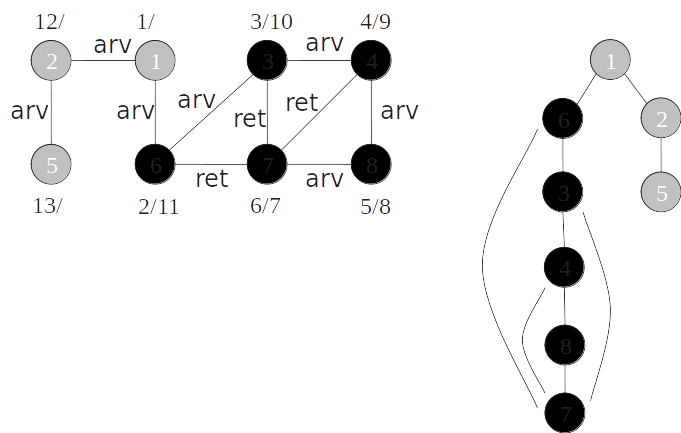
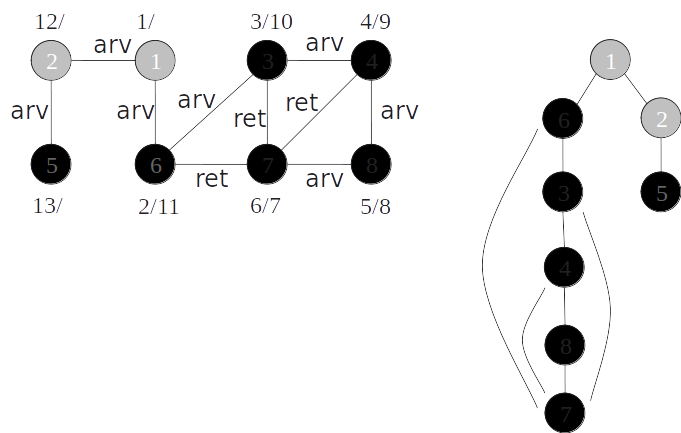
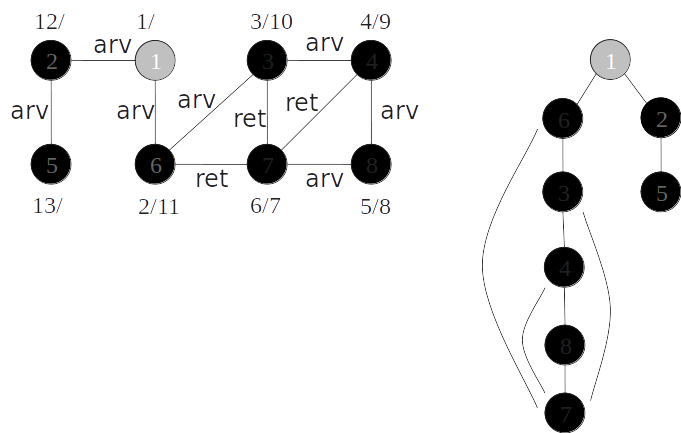
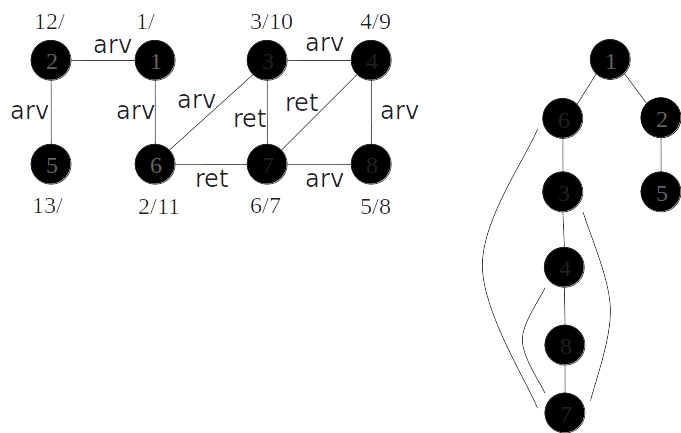
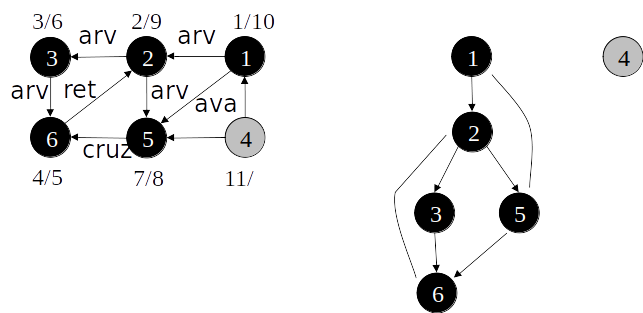
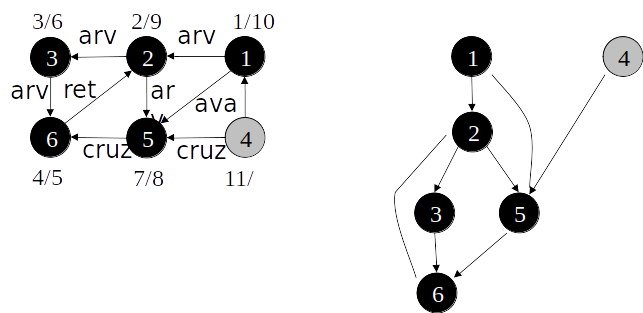
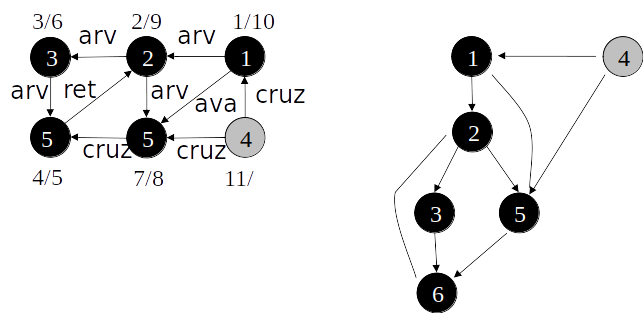
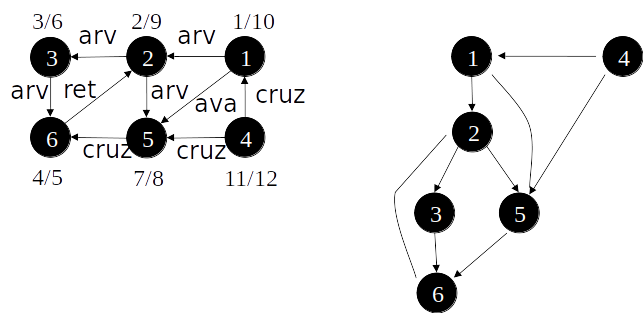
Classificação de arestas

• As arestas de um grafo podem ser classificadas conforme a sua árvore de busca em profundidade:
  • Arestas de árvore: arestas que ocorrem na árvore de busca em profundidade;
  • Arestas de retorno: arestas que ligam com um nó antecessor na árvore;
  • Arestas de avanço: arestas que ligam com um nó descendente na árvore;
  • Arestas de cruzamento: demais arestas.

Classificação de arestas

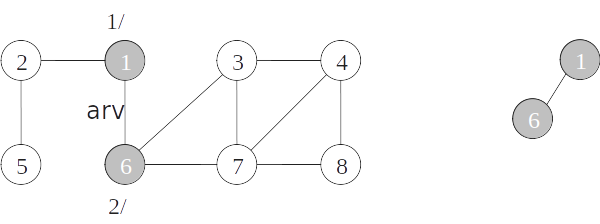
Classificação de arestas

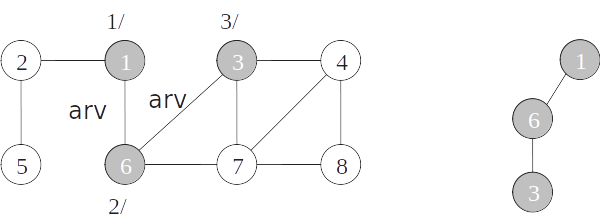
Classificação de arestas

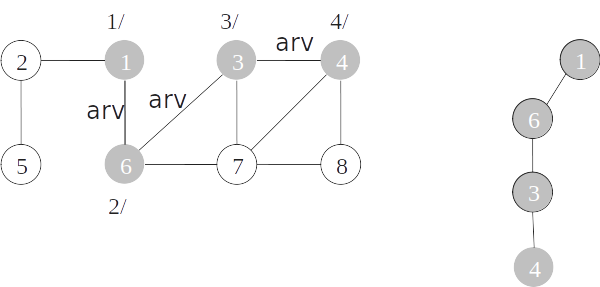
Classificação de arestas

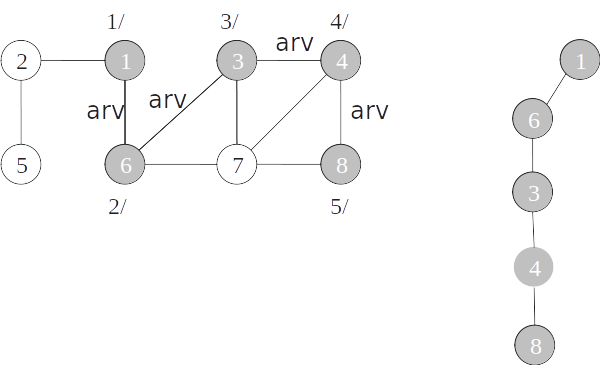
Classificação de arestas

Classificação de arestas

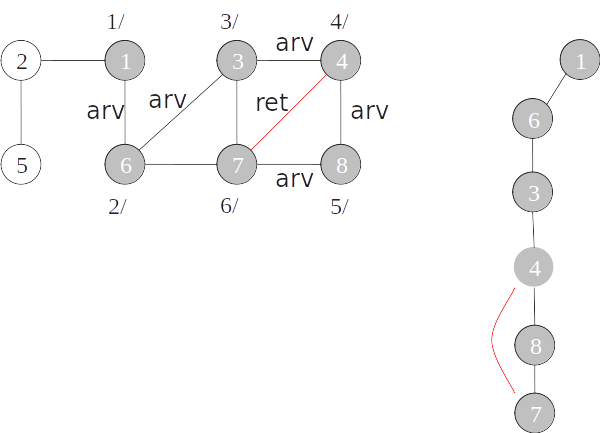
Classificação de arestas

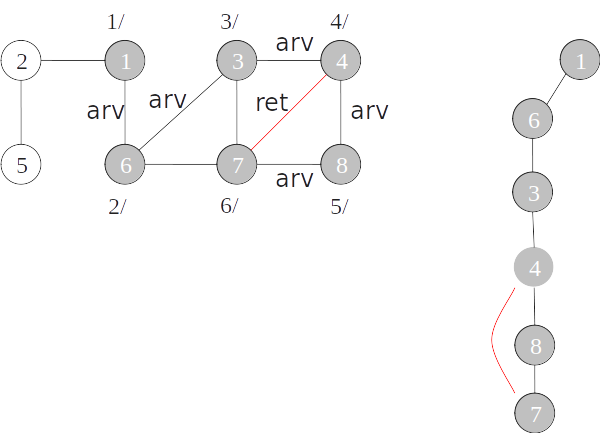
Classificação de arestas

Classificação de arestas

Classificação de arestas

Classificação de arestas

Classificação de arestas

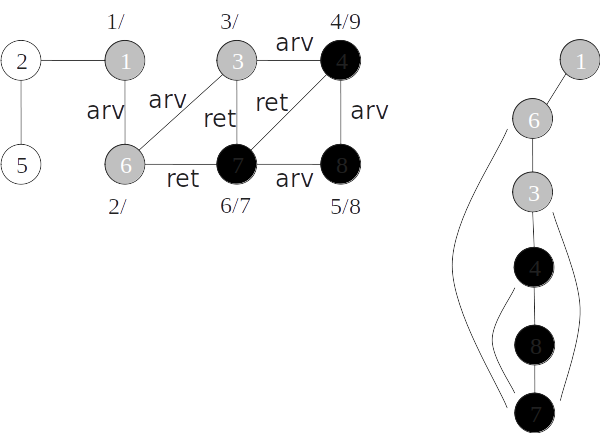
Classificação de arestas

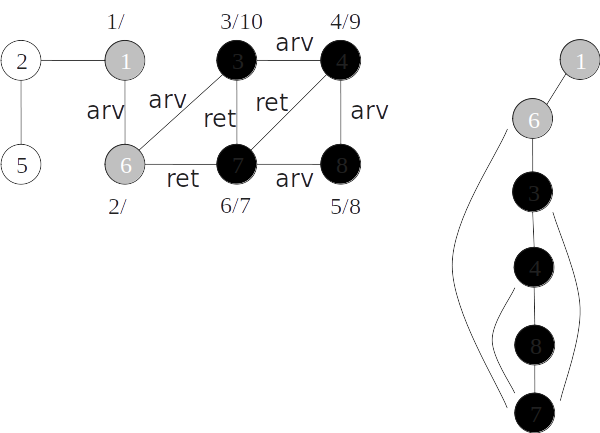
Classificação de arestas

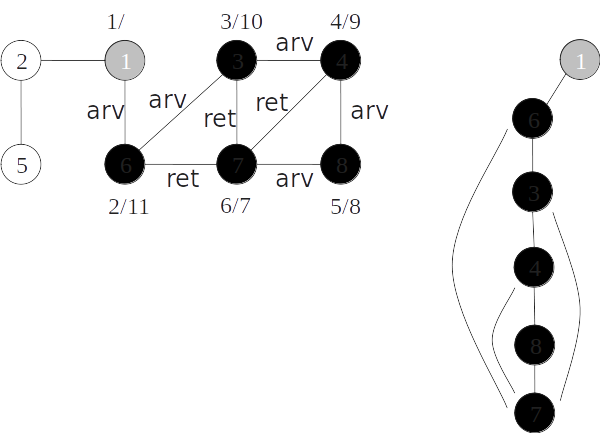
Classificação de arestas

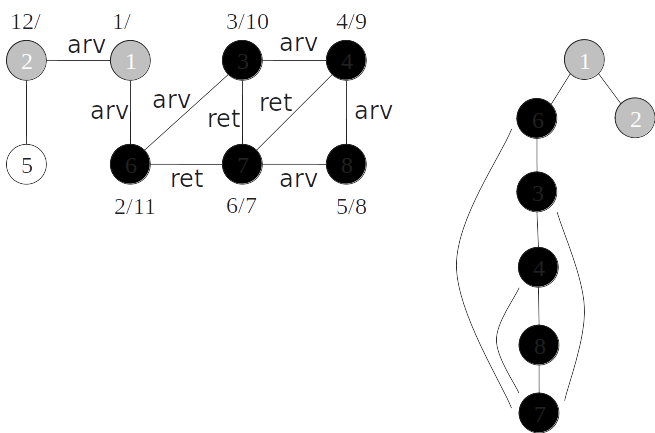
Classificação de arestas

Classificação de arestas

Classificação de arestas

Classificação de arestas

Classificação de arestas

• Em um grafo não orientado todas as arestas são de árvore ou de retorno.

• A algoritmo de busca em profundidade funciona igualmente bem para grafos direcionados.

• Nesse caso, podem ocorrer arestas de avanço e de cruzamento.

Busca em profundidade

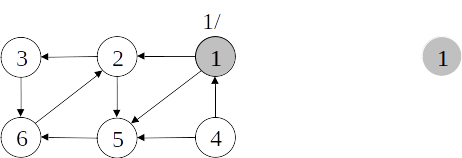
Busca em profundidade

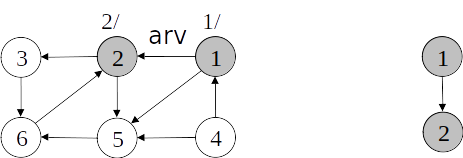
Busca em profundidade

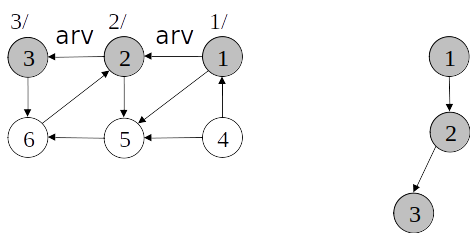
Busca em profundidade

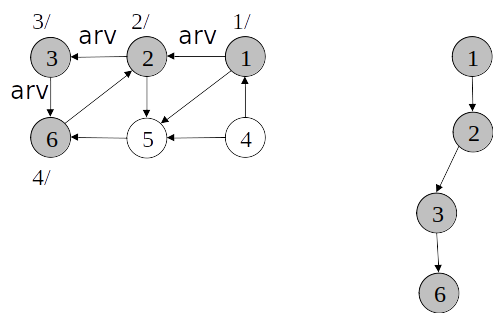
Busca em profundidade

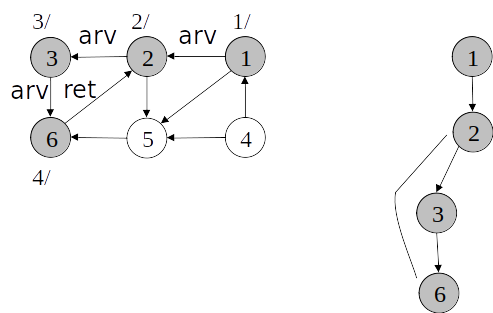
Busca em profundidade

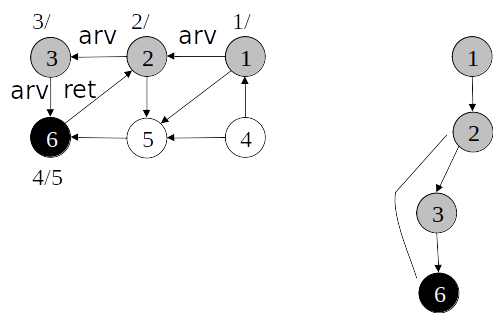
Busca em profundidade

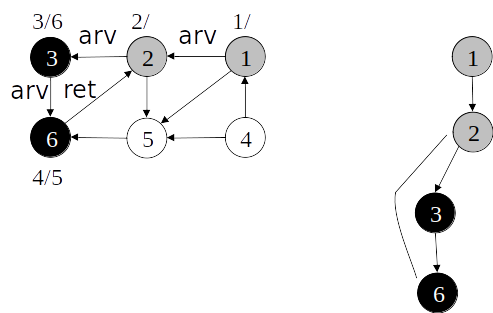
Busca em profundidade

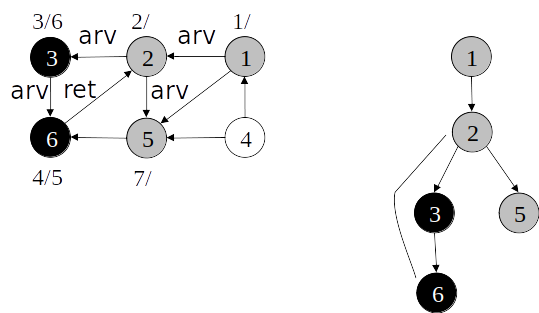
Busca em profundidade

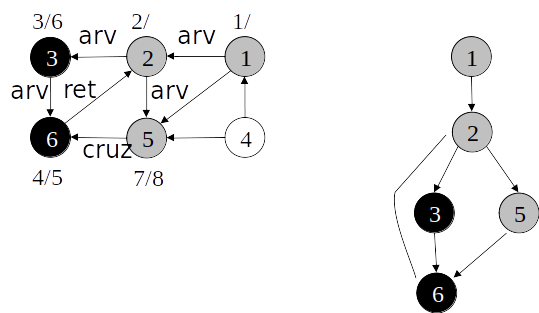
Busca em profundidade

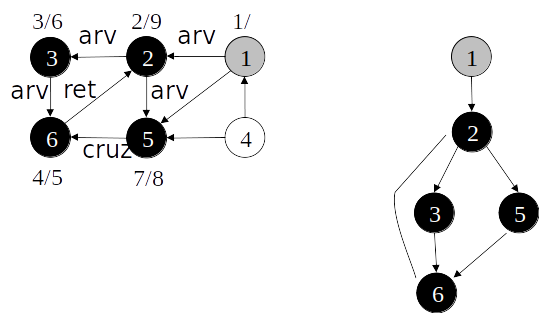
Busca em profundidade

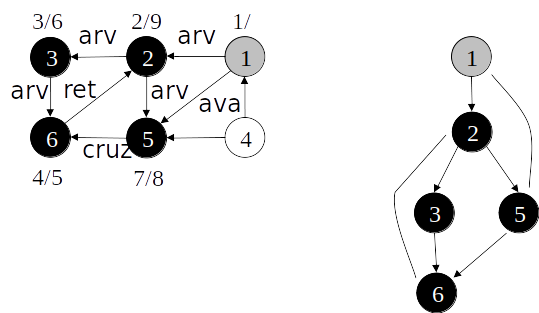
Busca em profundidade

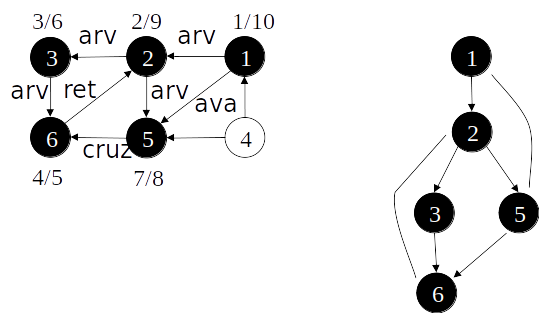
Busca em profundidade

Busca em profundidade

Busca em profundidade

Busca em profundidade

Detecção de ciclos

• A busca em profundidade pode ser usada para verificar se um grafo é acíclico ou contém um ou mais ciclos.
• Se uma aresta de retorno é encontrada durante a busca em profundidade em $G$, então o grafo tem ciclo.

Detecção de ciclos

• Um grafo direcionado $G$ é acíclico se e somente se a busca em profundidade em $G$ não apresentar arestas de retorno.
• O algoritmo de busca em profundidade pode ser modificado para detectar ciclos em grafos orientados simplesmente verificando se um vértice $w$ adjacente a $v$ possui cor cinza na primeira vez que a aresta $(v, w)$ é percorrida.

Detecção de ciclos

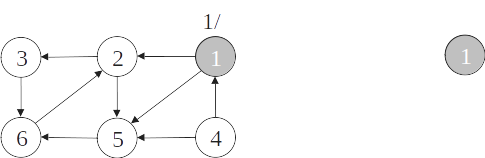
Detecção de ciclos

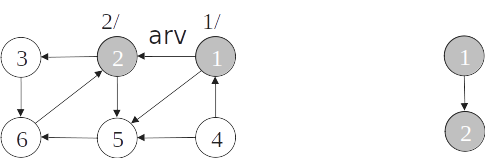
Detecção de ciclos

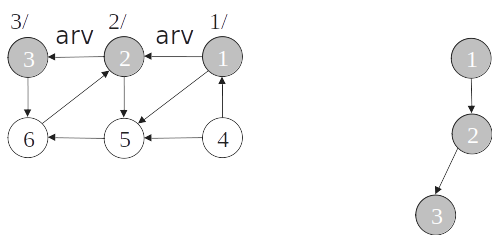
Detecção de ciclos

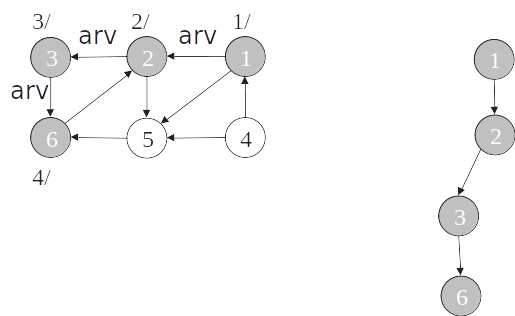
Detecção de ciclos

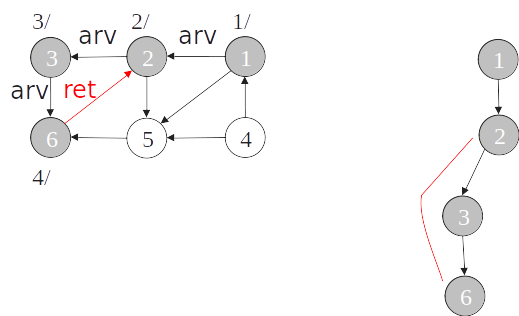
O grafo é cíclico

Detecção de ciclos

• Como o algoritmo de detção de ciclos é uma adaptação da busca em profundidade, é fácil perceber que a complexidade é a mesma daquele algoritmo

• Um grafo direcionado sem ciclos (acíclico) é também chamado de DAG (directed acyclic graph).

• Um DAG é diferente de uma árvore, pois um nó pode ter dois "pais".

Ordenação topológica

• DAGS podem ser utilizados, por exemplo, para indicar precedências entre eventos.
  • O grafo de disciplinas e recomendações de pré-requisitos, por exemplo, é um DAG.
• A ordenação topológica é uma ordenação linear de todos os vértices, tal que se $G$ contém uma aresta $(u,v)$ então $u$ aparece antes de $v$.
• Pode ser vista como uma ordenação de seus vértices, de tal forma que todas as arestas estão direcionadas da esquerda para a direita.
  • No caso do grafo de disciplinas, indica a ordem em que as disciplinas devem ser cursadas

Ordenação topológica

• A ordenação topológica de um dag pode ser obtida utilizando-se uma busca em profundidade.
• Para isso deve-se fazer o seguinte algoritmo:
  • Para um DAG, gaça uma busca em profundidade;
    • Quando um vértice é pintado de preto, insira-o na cabeça de uma lista de vértices;
    • Retorne a lista de vértices.

Ordenação topológica

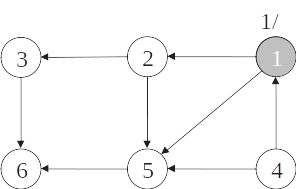
Ordenação topológica

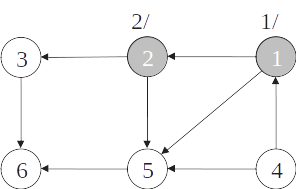
Ordenação topológica

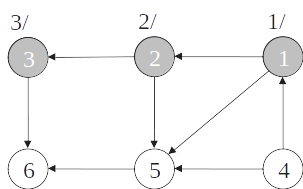
Ordenação topológica

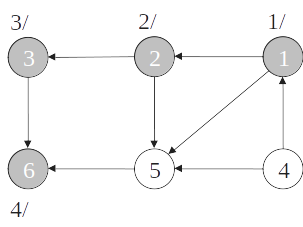
Ordenação topológica

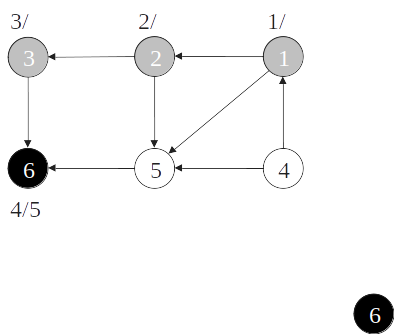
Ordenação topológica

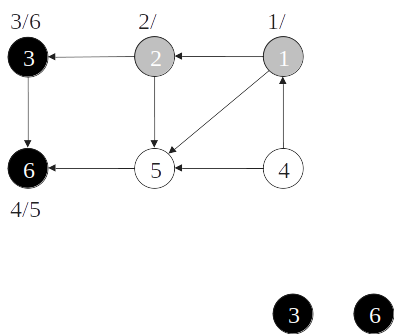
Ordenação topológica

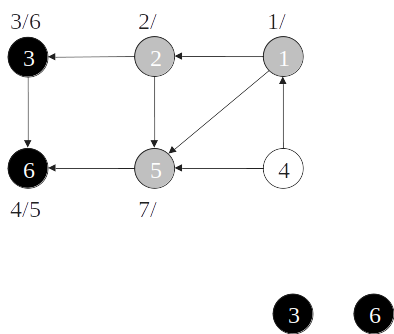
Ordenação topológica

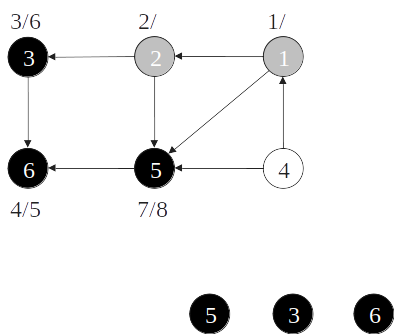
Ordenação topológica

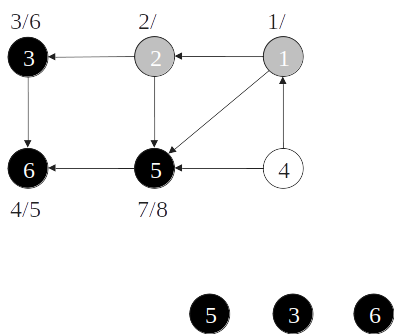
Ordenação topológica

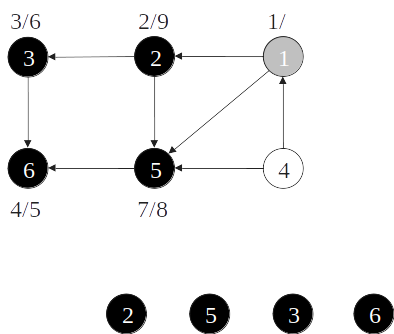
Ordenação topológica

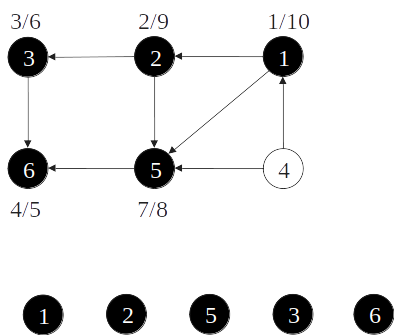
Ordenação topológica

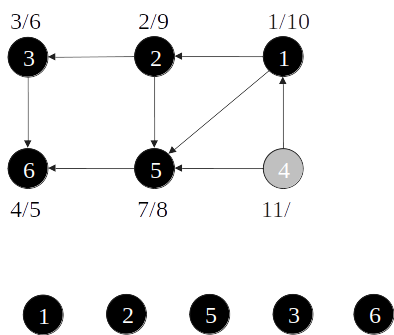
Ordenação topológica

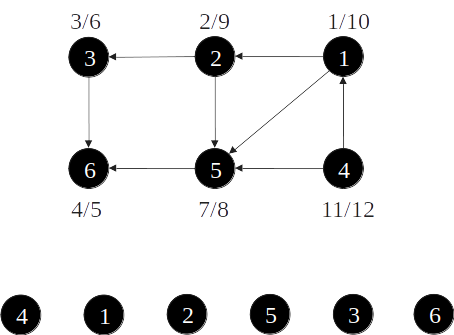
Ordenação topológica

Ordenação topológica

• Inserir um elemento na cabeça da lista é $O(1)$, e essa etapa é feita uma vez para cada nó.
• Portanto, o que domina a complexidade do algoritmo é a busca, e a ordenação topológica tem a mesma complexidade da busca em profundidade.

Componentes fortemente conectados

• Relembrando: Componentes fortemetne conectadas de um grafo $G = (V, E)$ é um conjunto maximal de vertices $C \subseteq V$, de tal maneira que todo o vértice de $C$ é alcançável de qualquer outro.

• Como encontrar as componentes fortemetne conectadas de um grafo?

Componentes fortemente conectados

• No grafo abaixo, se fizermos uma passada da busca em profundidade a partir de um nó amarelo, encontraremos a componente conexa amarela

• Entretanto, se começarmos por qualquer nó azul (ou verde), a busca irá percorrer também os nós amarelos

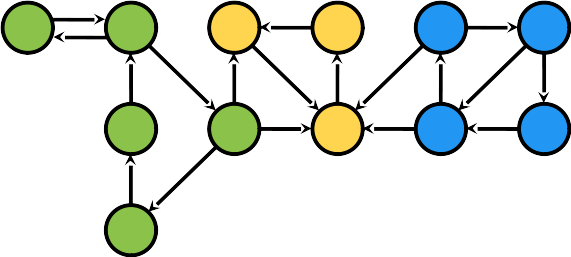
Componentes fortemente conectados

• Busca em profundidade pode encontrar componentes fortemente conexas em alguns casos.

• Entretanto, em alguns casos mais de uma (ou eventualmente o grafo inteiro) componente pode ser percorrida em uma execução da busca em profundidade a partir de um certo nó.

• Como podemos contornar esse problema?

Componentes fortemente conectados

• Se "comprimirmos" os nós de uma componente conexa em um único nó, o grafo será um DAG

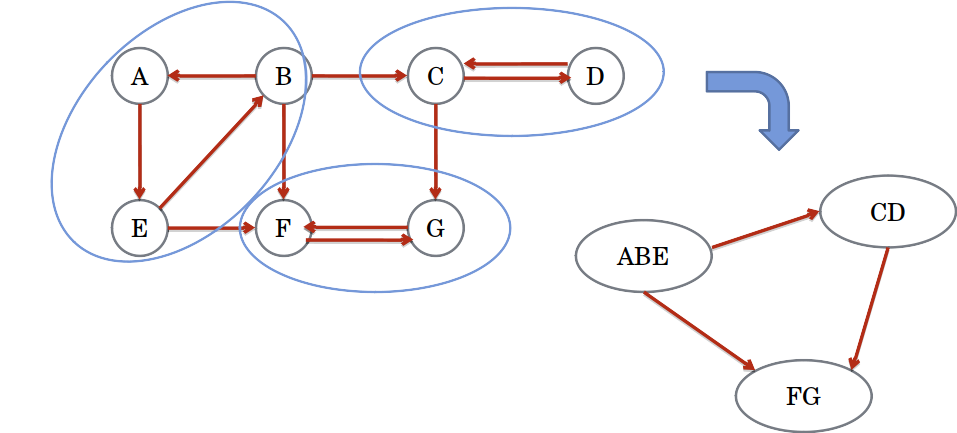
Componentes fortemente conectados

• Se "comprimirmos" os nós de uma componente conexa em um único nó, o grafo será um DAG

• Lema: Seja $C$ e $C'$ duas componentes distindas em um dígrafo $G$. Seja $u, v \in C$, e $u’, v’ \in C’$. Se $G$ contém um caminho $u-u’$, então $G$ não pode conter o caminho $v’v$.

• Prova:

  • Se $G$ conter ambos $u-u’$ e $v’v$, então eles são alcançáveis entre si.
  • Como qualquer vértice de uma componente conexa é alcançável a partir de outra do mesmo componente, então qualquer vértice de $C$ e $C'$ são alcançáveis entre si.
  • Então $C$ e $C'$ não são componentes conexas (contradição)

Componentes fortemente conectados

• A transposta $G^T$ (obtida por meio da mudança de orientação de cada aresta) de um grafo G tem as mesmas componentes conexas de $G

Componentes fortemente conectados

• Prova informal:
  • em uma componente conexa, os vértices forma um ciclo
  • reverter as arestas, continua um ciclo
  • O grafo comprimido de $G$ é um DAG
  • O grafo reverso ainda é um DAG
  • Então as componentes de $G$ e $G^T$ são as mesmas

Algoritmo de Kosaraju

• Excute a busca em profundidade e marque o tempo de finalização (em que passo o nó é pintado de preto) de cada vértice
• Construa $G^T$
• Execute a busca em profundidade novamente iterando sobre os nós em ordem reversa ao tempo de finalização calculado no passo 1
• Cada subcomponente encontrada na segunda iteração será uma componente fortemente conectada

Algoritmo de Kosaraju

• Calcule o tempo de finalização de cada vértice usando busca em profundidade.

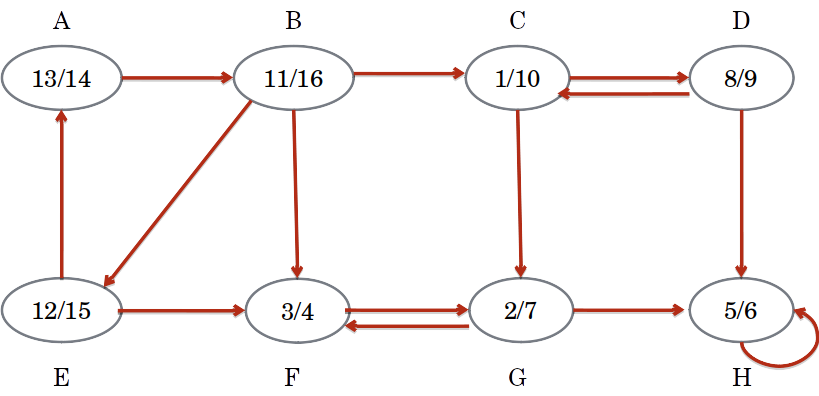
Algoritmo de Kosaraju

• Reverter as Arestas
  

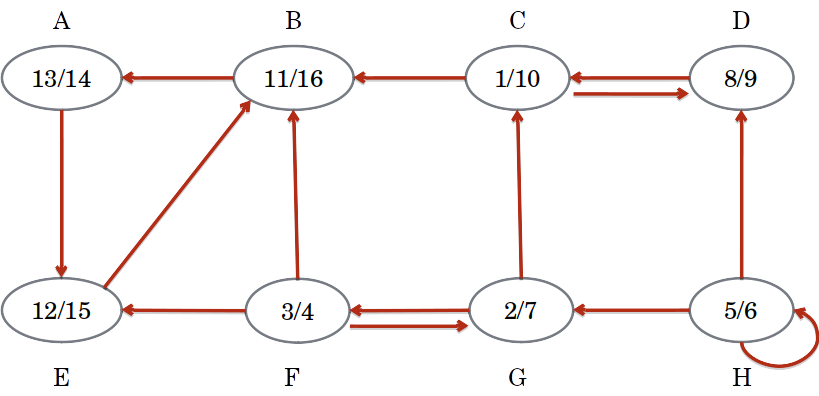
Algoritmo de Kosaraju

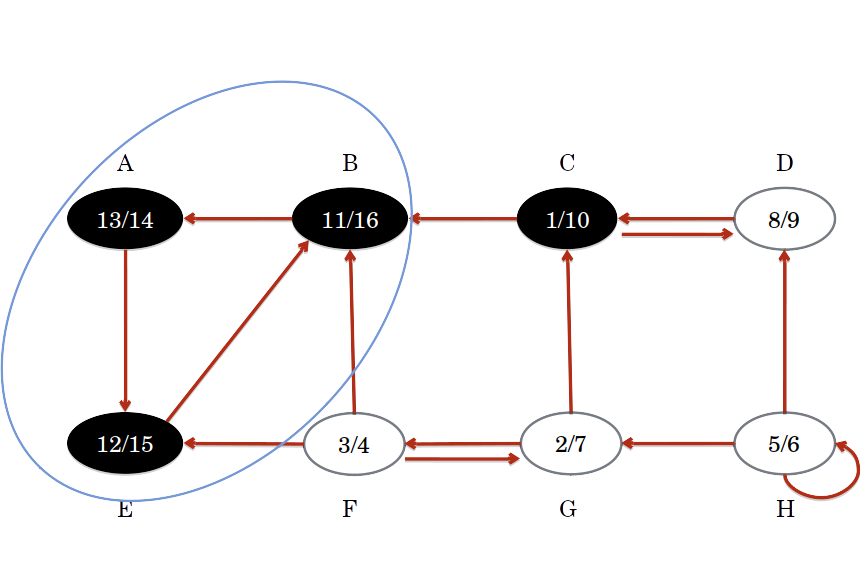
Algoritmo de Kosaraju

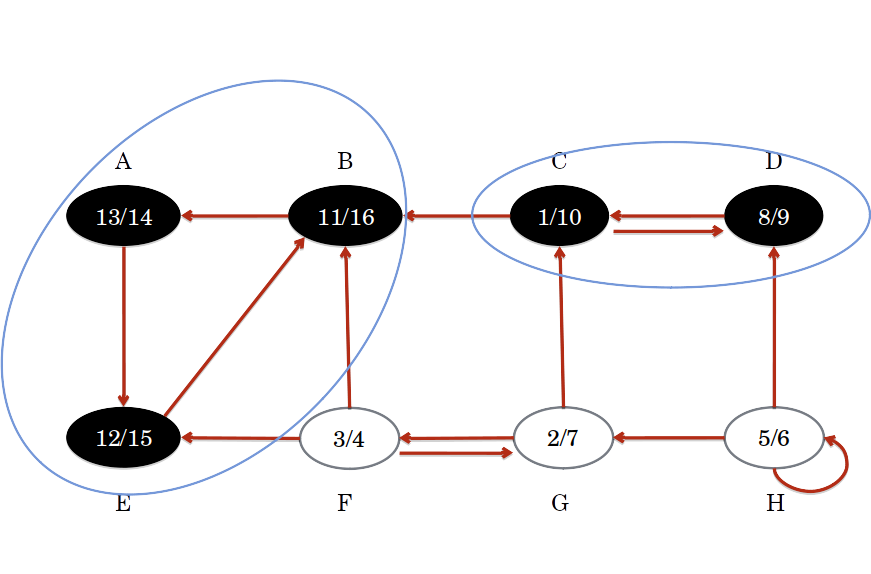
Algoritmo de Kosaraju

Algoritmo de Kosaraju

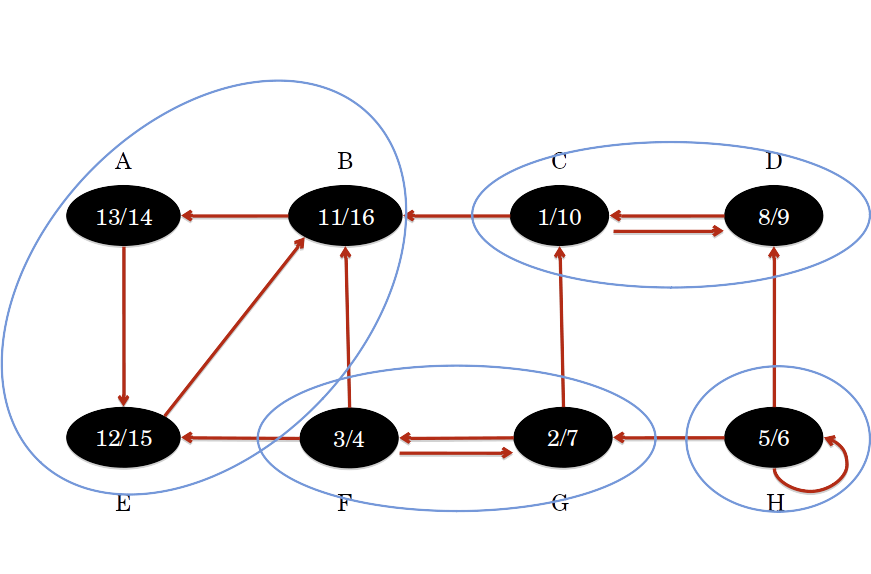
Algoritmo de Kosaraju

• Por que funciona?
  • As arestas que conectam duas componentes são exploradas depois que as arestas de um componente conexa são exploradas.
  • $G^T$ pode ser comprimido em um DAG
  • Usar a ordem reversa na sugunda busca em profundidade implica que estamos percorrendo as areastas do DAG em ordem topológica reversa.
  • Como estamos percorrendo os os nós em ordem reversa de prioridade, não corremos o risco de "pular" de uma componente fortemente conectada para outra sem iniciar uma nova busca em profundidade a partir de um outro nó
  • Todos os vértices das componentes já visitadas estão marcados como visitados

Algoritmo de Kosaraju

• Criar o grafo reverso tem custo $O(|E|)$
• Executamos duas passagens completas da busca em profundidade, portanto a complexidade é a mesma dessa busca.