Algoritmos Gulosos

• Constrói uma solução por meio de uma sequência de decisões

  • visa melhorar o cenário a curto prazo
  • em geral, não há garantias que levará ao melhor resultado global (e geralmente não encontra a solução ótima)

• Geralmente são rápidos e fáceis de implementar

  • A complexidade geralmente é fácil de analisar
  • Não é trivial provar é de fato ótima

Algoritmos Gulosos

• Princípio:
  • Faça uma escolha de cada vez
  • Nunca retroceda
  • Espere que a estratégia funcione

Algoritmos Gulosos

• Algoritmos gulosos são eficientes se:

  • A cada passo, fazemos a melhor escolha
  • O problema tem sub-estrutura ótima

• Problemas que tem sub-estrutura ótima, a solução ótima do problema é composta pelas soluções ótimas dos sub-problema menores

Sacando dinheiro no caixa

• Dados:
  • um certo valor $n$ que quero sacar no caixa eletrônico
  • As notas disponíveis naquele caixa eletrônico (por exemplo, $50, $10, $5 e $1)
• Como entregar o dinheiro usando a menor quantidade de notas?
• Mais formalmente, encontrar os valores para $a_1$, $a_2$, $a_3$ e $a_4$ tal que:
  $n=a_1\times 50+a_2\times 10+a_3\times 5+a_4$
• Minimizando
  $\min\sum a_i$

Sacando dinheiro no caixa

• Como resolver?
• Uma solução força bruta é:
  • no máximo, o número de notas é $n$
  • testar todas as combinações em que $a_1\leq n$, $a_2\leq n$, $a_3\leq n$ e $a_4\leq n$
  • selecionar as combinações em que $n=a_1\times 50+a_2\times 10+a_3\times 5+a_4$
  • Selecionar a que $\sum a_i$ é mínimo
• Complexidade: temos que gerar todas as combinações de $n$ quatro a quatro, então a complexidade é $\Theta(n^4)$

Sacando dinheiro no caixa

• Uma estratégia gulosa é atribuir o máximo possível da nota de maior valor

ContaDinheiro(n)
i = 1
notas = [50,10,5,1]
Enquanto (i <= tamanho(notas))
  a[i] = n % notas[i] //divisão inteira
  n = n - a[i]

Sacando dinheiro no caixa

• É fácil ver que a complexidade é $O(|notas|)$
• Ele está correto?
• Ele é ótimo?

Sacando dinheiro no caixa

• Ele está correto?
• A invariante de laço é que, antes do passo $k$, $n_k = n_{k-1} + \sum_i^{k-i} notas[i]\times a[i]$

$\begin{aligned} n_{k} & = n_k + \sum_i^{k} notas[i] \times a[i] \\ & = \left(n_{k-1} - (notas[k] \times a[k])\right) + \sum_i^{k} notas[i] \times a[i] \\ & = n_{k-1} + \left(\sum_i^{k} notas[i] \times a[i] - (notas[k] \times a[k])\right) \\ & = n_{k-1} + \sum_i^{k-i} notas[i]\times a[i] \end{aligned}$

Sacando dinheiro no caixa

• Ele é ótimo?
• Considere que temos apenas notas de $1 e $5.
  • Se $n < 5$, só podemos atribuir notas de $1
  • Se $n \geq 5$, seja $x$ o número de notas de $5 atribuídas pela estratégia gulosa e $y$ o número de notas de $1
  • Para torcar uma nota de $5, precismos de 5 vezes o número de notas de $1. Se trocarmos $x' \leq x$ das notas de $5 por notas de $1, a soma de notas é $x-x'+y+(5x') = x+y+(4x')$
  • Portanto o número de notas não aumenta apendas se fizermos 0 trocas
  • Podemos estender esse racicínio para as demais notas.

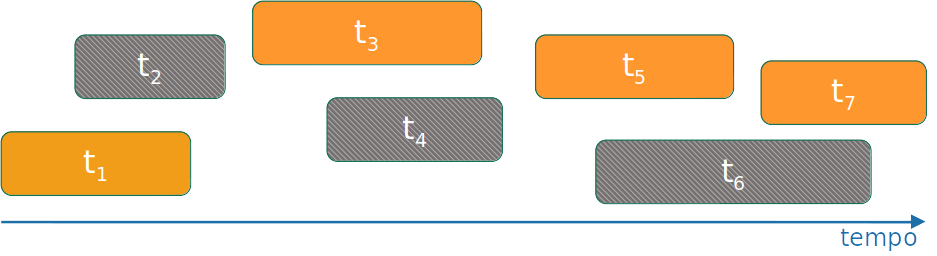
Escalonamento de tarefas

• Seja um conjunto de tarefas $T = \{t_1,\cdots,t_n\}$ a serem executas
  • Cada tarefa $t_i \in T$ tem um tempo inicial $s_i$ e tempo final $f_i$.
  • Se selecionada, essa tarefa ocupa o intervalo de tempo $[s_i,f_i)$

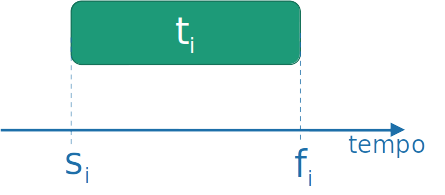
Escalonamento de tarefas

• Duas tarefas $t_i$ e $t_j$ são compatíveis se os intervalos $[s_i,f_i)$ and $[s_j,f_j)$ não se sobrepõem

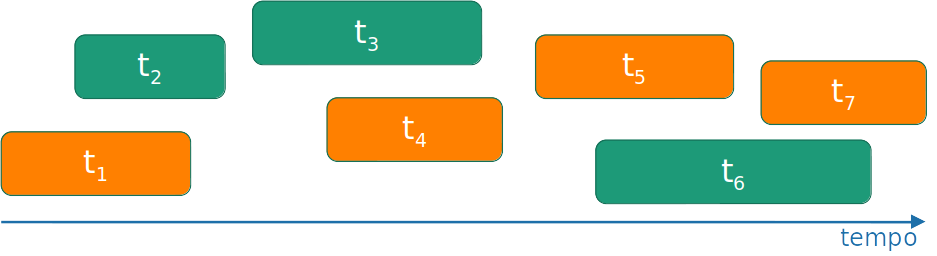
Escalonamento de tarefas

Dado um conjunto $T={t_1,...,t_n}$ com $n$ tarefas em que cada $t_i \in T$ tem um tempo inicial $s_i$ e um tempo final $f_i,$ encontrar o maior subconjunto de tarefas mutuamente compatíveis.

Algoritmo guloso

• Selecione a atividade que você pode adicionar com o menor tempo de finalização.
• Repita

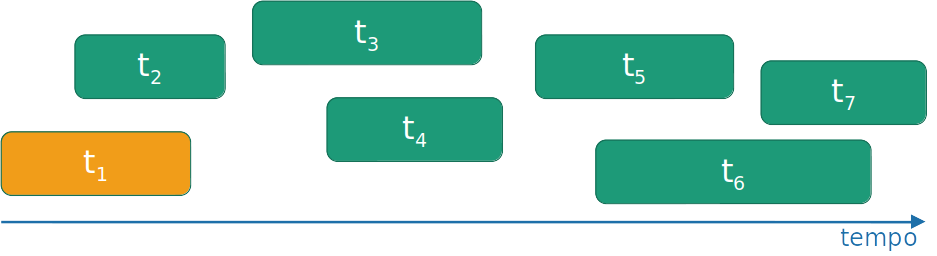
Algoritmo guloso

• Selecione a atividade que você pode adicionar com o menor tempo de finalização.
• Repita

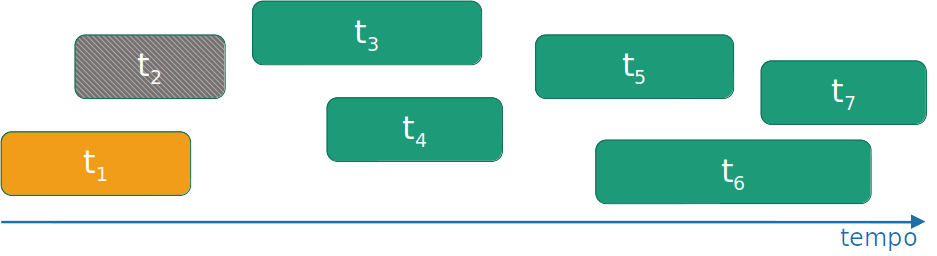
Algoritmo guloso

• Selecione a atividade que você pode adicionar com o menor tempo de finalização.
• Repita

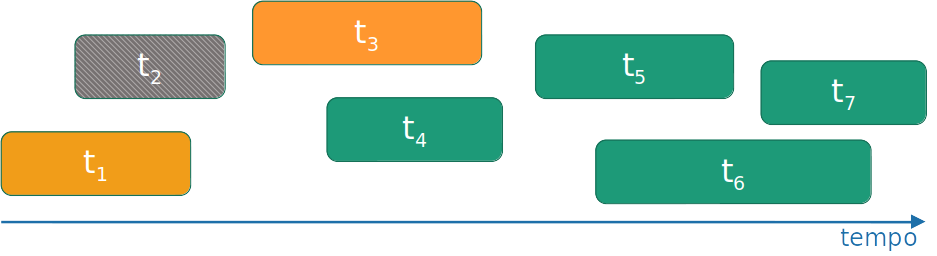
Algoritmo guloso

• Selecione a atividade que você pode adicionar com o menor tempo de finalização.
• Repita

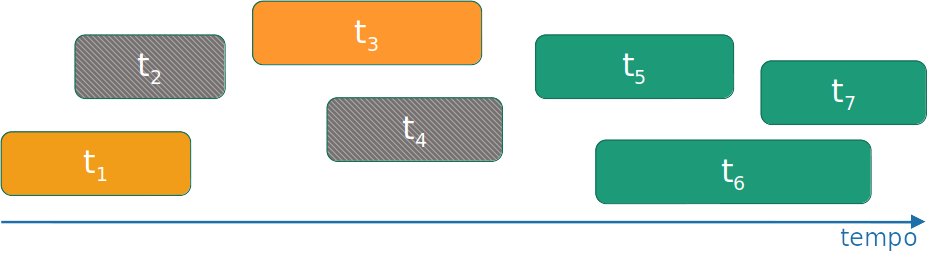
Algoritmo guloso

• Selecione a atividade que você pode adicionar com o menor tempo de finalização.
• Repita

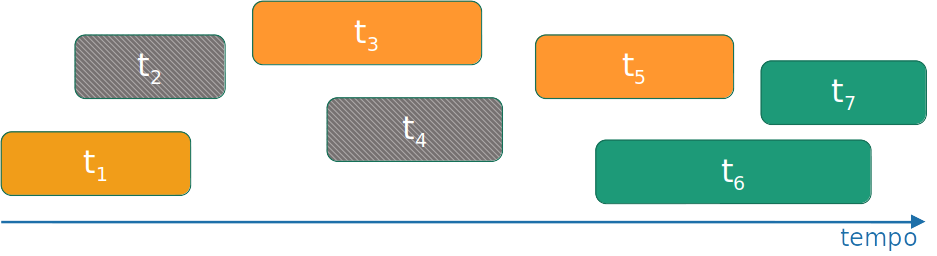
Algoritmo guloso

• Selecione a atividade que você pode adicionar com o menor tempo de finalização.
• Repita

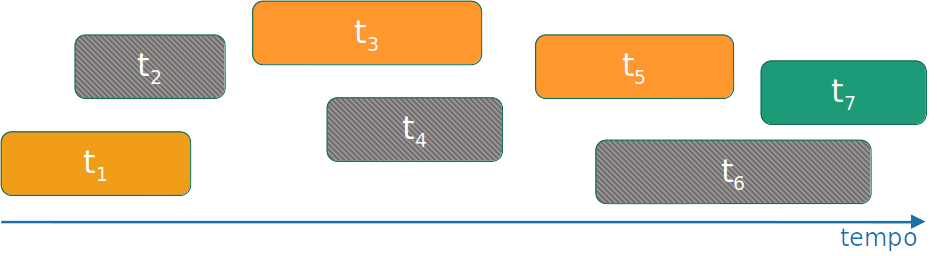
Algoritmo guloso

• Selecione a atividade que você pode adicionar com o menor tempo de finalização.
• Repita

Algoritmo EscalonaCompatível

Algoritmo EscalonaCompatível

• É fácil notar que o laço da linha 5 é executado em $O(n)$, pois percorre a lista de tarefas

• A complexidade do algotirmo é dada pela ordenação das tarefas, que pode ser executada em $O(n\log n)$

Por que é um algoritmo guloso?

• Em cada passo, o algoritmo faz uma escolha:
  • Examina uma tarefa de cada vez: ou adiciona a tarefa na lista de compatíveis, ou descarta se não for compatível
  • Deixa várias possibilidades para as escolhas das tarefas futuras
  • Espera que essa escolha seja a melhor possível (uma vez que a tarefa é adicionada ou descartada, não volta atrás para ver se poderia fazer uma escolha melhor).

Lema

Dado conjunto $T={t_1,...,t_n}$ com $n$ tarefas em que cada $t_i \in T$ tem um tempo inicial $s_i$ e um tempo final $f_i$, o algoritmo EscalonaCompativel(T,n) retorna uma solução ótima para o problema de Escalonamento de tarefas compatíveis.

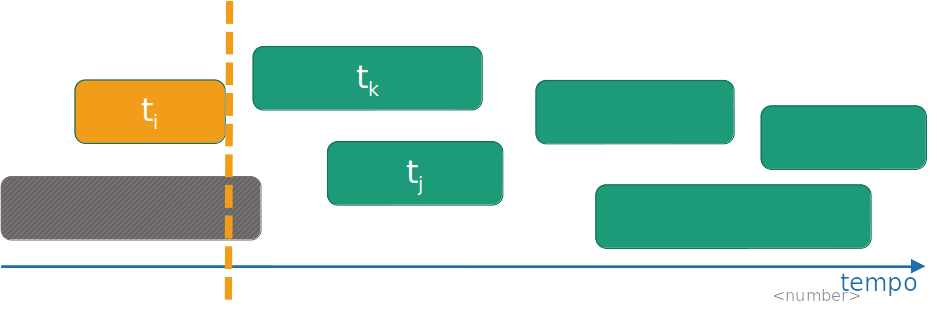
Prova

• Suponha que acabamos de selecionar $p_i$, e ainda existe uma solução $S$ que extende nossas escolhas atuais

• Considere também que a próxima tarefa com menor tempo de término é a $t_k$

Prova

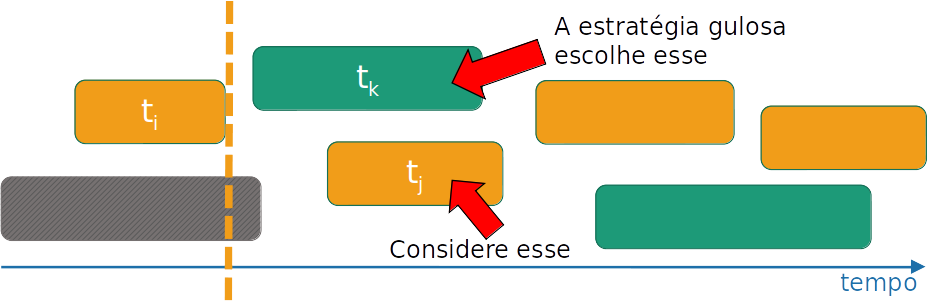
• Se $t_k \in S$, então ela será a próxima selecionada, de acordo com a estratégia.
• Se $\exists S | t_k \notin S$, considere a segunda atividade $t_j$ com menor tempo de término após $t_i$, e assuma que $t_j \in S$

Prova

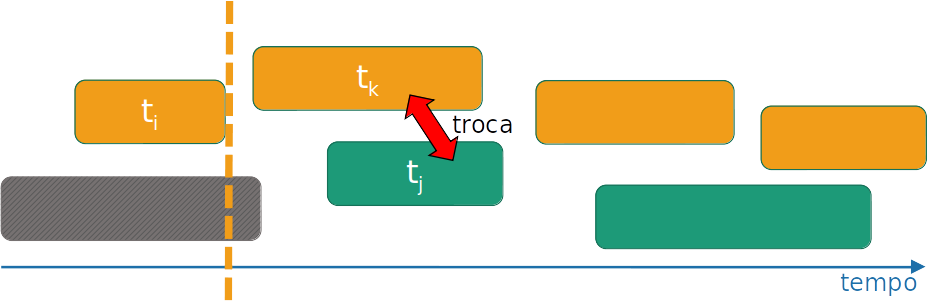
• Se trocarmos $t_k$ por $t_j$, temos que:
  • $t_k < t_j$, então a troca não interfere em nada após $t_j$
  • trocamos uma tarefa por outra, o que não afeta a quantidade de tarefas da solução
• Portanto, a solução que inclui $t_k$ também é ótima!

Prova

• Nós nunca excluímos uma solução ótima
• Ao final da execução do algoritmo, nós obtemos uma solução
• Então essa solução deve ser ótima!

Indução

• Hipótese indutiva: ao adicionar o $k$-ésima tarefa, existe uma solução ótima que extende a solução atual
• Caso base: Ao adicionar zero atividades, existe uma solução ótima que pode ser extendida
• Passo de Indução: acabamos de verificar
• Conclusão: após adicionar a última atividade, existe uma solução ótima que extende a solução atual; além disso, ela é a única que extende a solução atual; então ela é ótima.

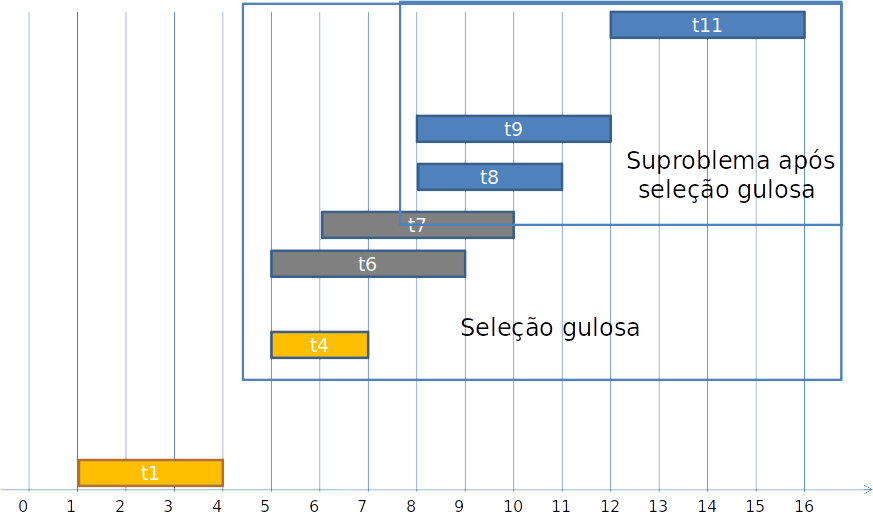
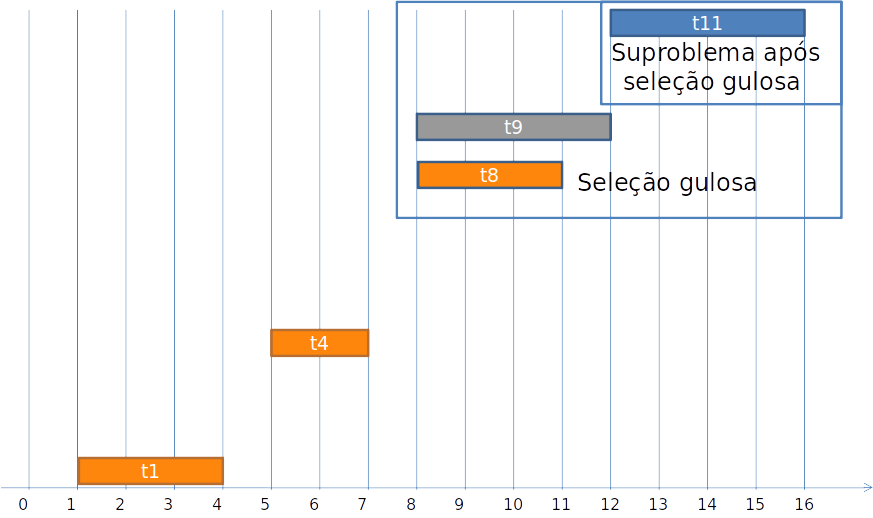
Sub-estrutura ótima

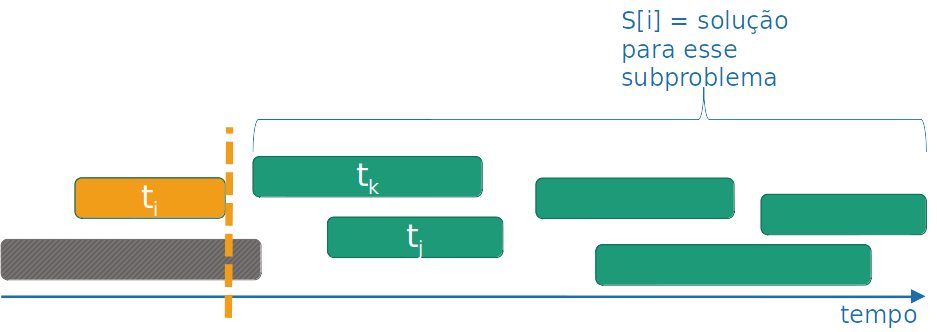
• Seja $|S[i]|$ número de atividades que podem ser feitas após a tarefa $i$.

• Esse número é dado pela solução do subproblema após a tarefa $t_i$

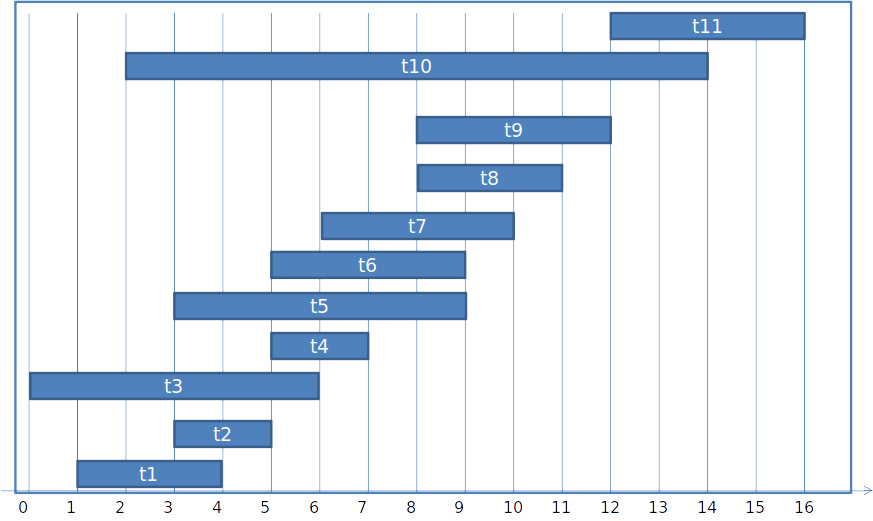
Sub-estrutura ótima

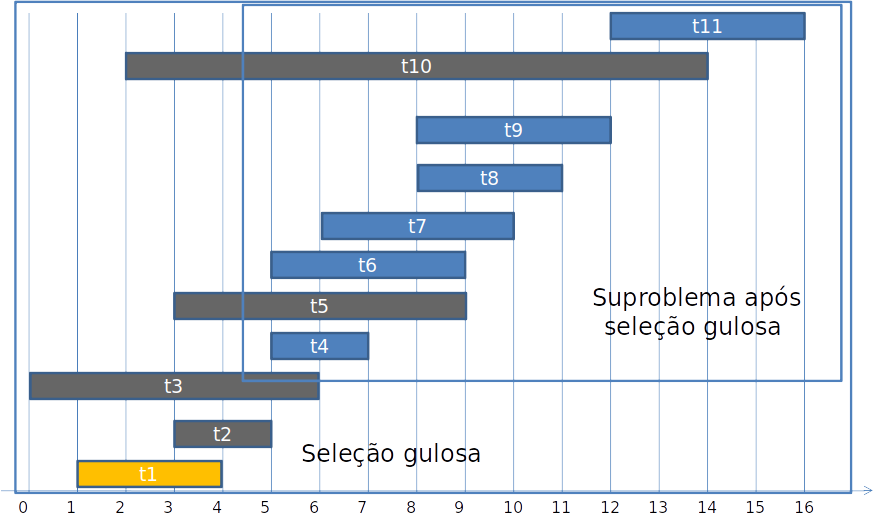
Sub-estrutura ótima

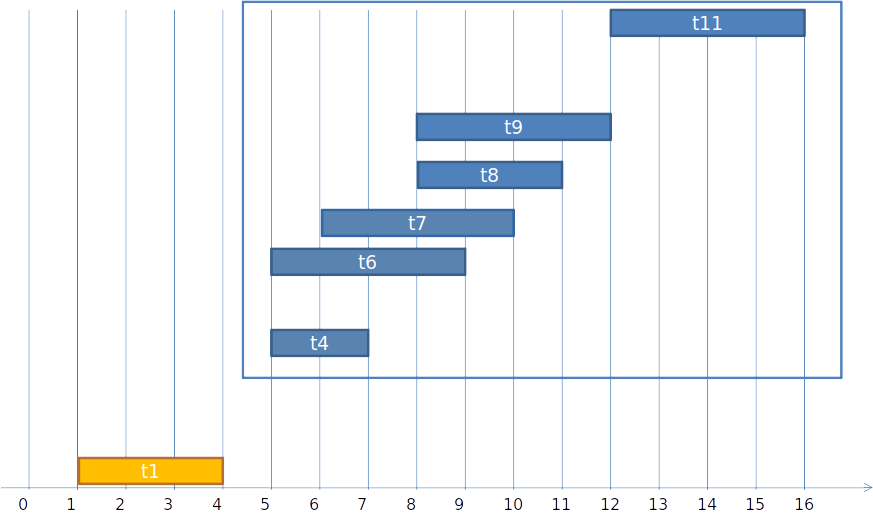
Sub-estrutura ótima

Sub-estrutura ótima

Sub-estrutura ótima

Sub-estrutura ótima

Sub-estrutura ótima

Problema da Mochila fracionária

• O problema da mochila é um dos problemas clássicos em computação
• Itens tem pesos e valores, e a mochila tem uma capacidade máxima
• Como escolher itens para colocar na mochila de maneira a maximizar o valor
• Mochila binária
  • Você só pode pegar ou deixar um item
• Mochila fracionária
  • Você pode pegar partes (frações) de um item

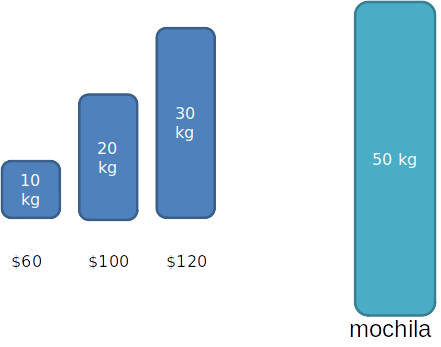
Mochila fracionária

Dado um conjunto $I={1,2,\cdots,n}$ de $n$ itens em que cada $i \in I$ tem um peso $w_i$ e um valor $v_i$ associados e dada uma mochila com capacidade de peso $W$, selecionar frações $f_i \in [0,1]$ dos itens tal que $\sum_{i=1} f_iw_i \leq W$ e $\sum_{i=1} f_iw_i$ é máximo.

Mochila fracionária

Mochila fracionária

• Uma estratégia gulosa óbvia é sempre escolher o item de maior valor que cabe na mochila.

• No exemplo anterior, escolheriamos os itens 3 primeiro e em seguida o item 2, esgotando a capacidade da mochila com um valor total de $220

Mochila fracionária

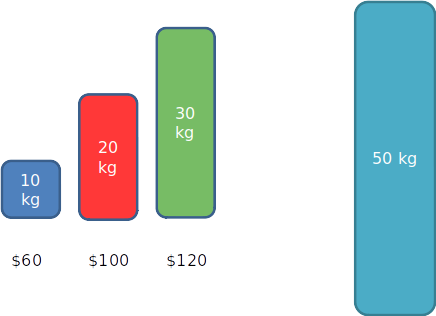
Mochila fracionária

• Entretanto, essa estratégia não é ótima.

• Se escolhermos os itens 1, 2 e 2/3 do item 3, esgotando a capacidade da mochila, o valor total é $240

Mochila fracionária

Mochila fracionária

• A estratégia falha pois ela ignora completamente a capacidade da mochila.
• Intuitivamente, o que queremos escolher os itens que tem o melhor custo-benefício, ou seja, o maior valor por unidade de peso.
• Uma outra estratégia gulosa é escolher os itens com a maior razão valor/peso

Mochila fracionária

Mochila fracionária

• O algoritmo consiste de dois passos principais:
  • a ordenação do vetor de objetos e
  • a posterior iteração sobre esse vetor.
• O primeiro passo toma tempo $O(n∗\log(n))$ já que é feita uma ordenação em um array de $n$ elementos utilizando um algoritmo de ordenação.
• O segundo passo toma tempo $O(n)$, já que a iteração é feita no número $n$ de objetos. Assim a complexidade geral do algoritmo será $O(n∗\log(n)+n)=O(n∗\log(n))$

Mochila fracionária - corretude

• O que o algoritmo faz é selecionar os objetos em ordem decrescente de $vi/w_i$ até preencher toda a mochila.

• Queremos provar que esta estratégia produz uma solução ótima para o problema da mochila fracionária.

• Suponha sem perda de generalidade que os objetos disponíveis são numerados em ordem decrescente de valor por unidade de peso, isto é:

$\frac{v_1}{w_1} \geq \frac{v_2}{w_2} \geq \cdots \geq \frac{v_n}{w_n}$

Mochila fracionária - corretude

• Considere $f=(f_1,f_2,\cdots,f_n)$ a solução produzida pelo algoritmo. - Se todos os $f_i$ são iguais a 1, a solução é claramente ótima.
• Caso contrário, seja $j$ o menor índice cujo $f_j<1$. Observando a forma como o algoritmo trabalha fica claro que $f_i=1$ quando $i<j$, e que $f_i=0$ quando $i>j$, e ainda $\sum x_iw_i=W$.

Mochila fracionária - corretude

• Agora considere o valor da solução $f$ como sendo $V(f)=\sum f_iv_i$ .

• Agora considere $g=(g_1,g_2,\cdots,g_n)$ qualquer outra solução viável. - Como $g$ é viável então $\sum g_iw_i=W$, com este fato notamos também que $\sum (f_i - g_i)w_i \geq 0$.

• Considere o valor da solução $g$ como sendo $V(g)=\sum g_iv_i$, assim temos

$V(f)−V(g)=\sum (f_i−g_i)vi= (x_i−y_i)w_i\frac{v_i}{w_i}$

Mochila fracionária - corretude

• Quando $i<j, f_i=1$ então $f_i−g_i$ é positivo ou zero, enquanto $v_i/w_i\geq v_j/w_j$
• Já quando $i>j, fi=0$ e então $f_i−g_i$ é negativo ou zero, enquanto $v_i/w_i\geq v_j/w_j$
• Finalmente, $i=j, v_i/w_i=v_j/w_j$.
• Dessa forma para todo $i=1,2,\cdots,n$ temos que $(f_i−g_i)(v_i/w_i)\geq(f_i−g_i)(v_j/w_j)$.

Mochila fracionária - corretude

• Então podemos concluir que
  $V(f)−V(g)\geq(v_j/w_j)\sum(f_i−g_i)w_i\geq0$
• Em outras palavras, o valor de $f$ é maior ou igual ao valor de $g$
• Assim provamos que não existe solução viável que possua valor estritamente maior que o valor $V(f)$ da solução encontrada pelo algoritmo, logo $f$ é uma solução ótima para o problema da mochila fracionária.