Análise de Algoritmos
Ronaldo Cristiano Prati
Bloco A, sala 513-2
ronaldo.prati@ufabc.edu.br
Árvore Geradora Mínima
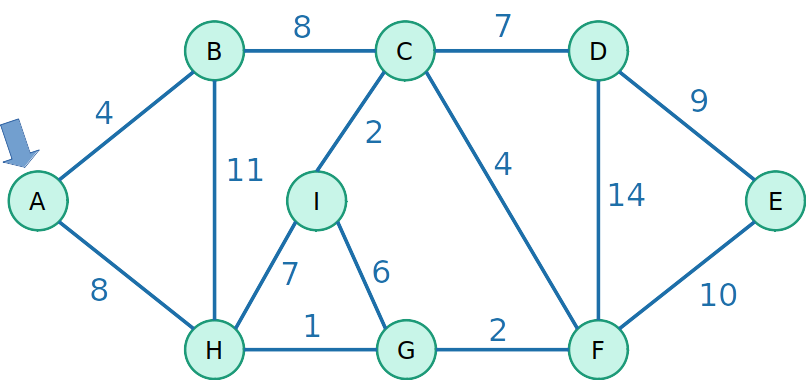
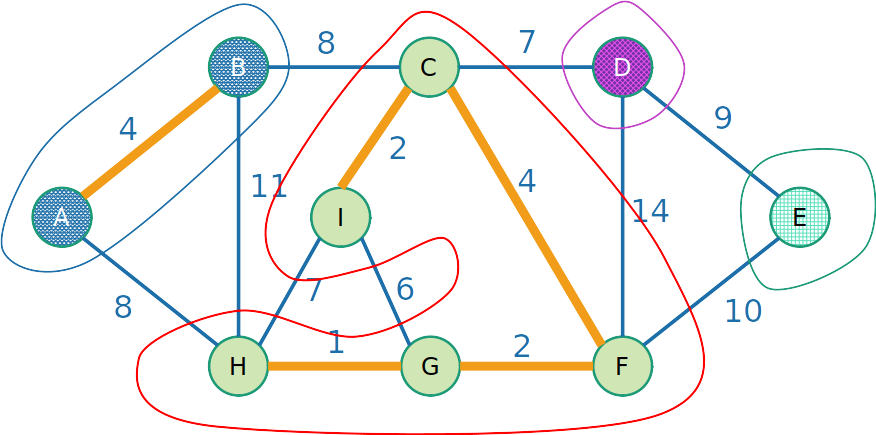
- Considere um grafo não direcionado com pesos, como mostrado no exemplo:
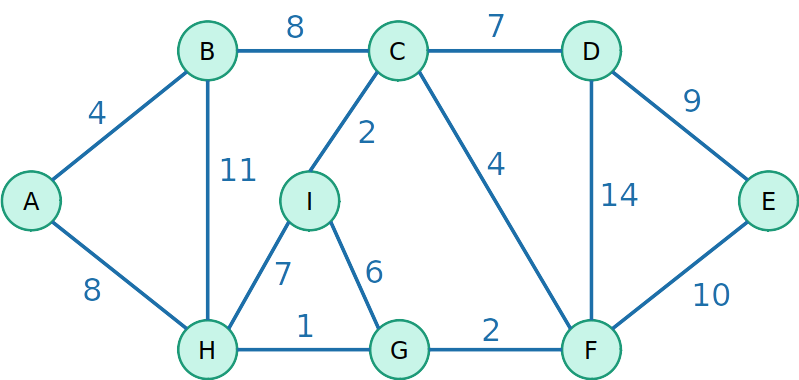
Árvore Geradora
-
Uma árvore T é grafo que não tem ciclos
-
Uma árvore geradora é uma árvore formada por um subconjunto de areastas de um grafo que conecta todos os nós do grafo
-
O custo w(T) de uma árvore geradora é a soma dos pesos de suas arestas
Árvore Geradora
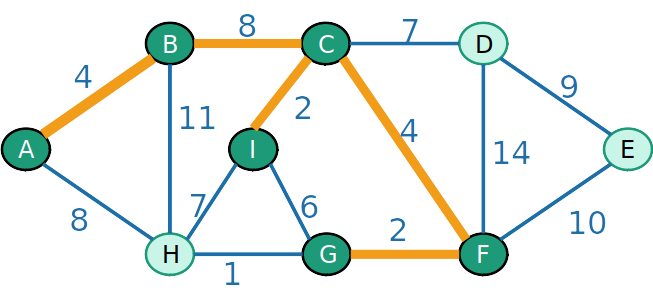
- Por exemplo, a árvore geradora destacada em laranja tem um custo w(T)=67
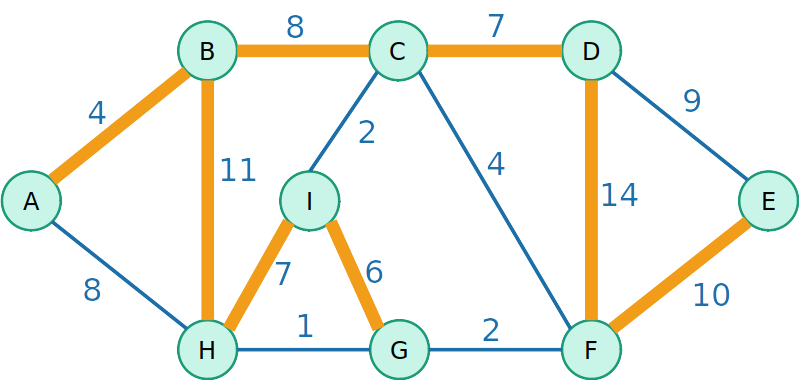
Árvore Geradora
- Essa outra árvore geradora destacada em laranja tem um custo w(T)=37
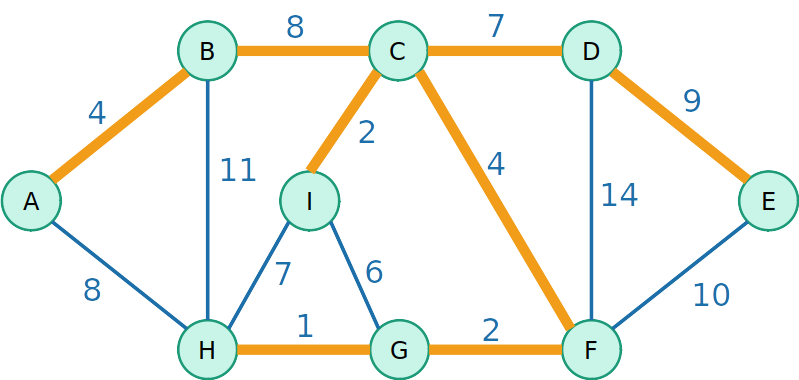
Árvore Geradora Mínima
-
Uma árvore geradora mínima (MST) é uma árvore formada por um subconjunto de arestas de um grafo que conecta todos os vértices do grafo e tem custo mínimo
-
Muitas aplicações:
- Projeto de redes
- Análise de grupos genéticos
- Segmentação de imagens
- Primitiva para outros algoritmos de grafos
Como gerar uma MST
- Vamos estudar duas estratégias gulosas para encontrar uma MST
Corte
- Um corte é uma partição dos vértices em duas partes:
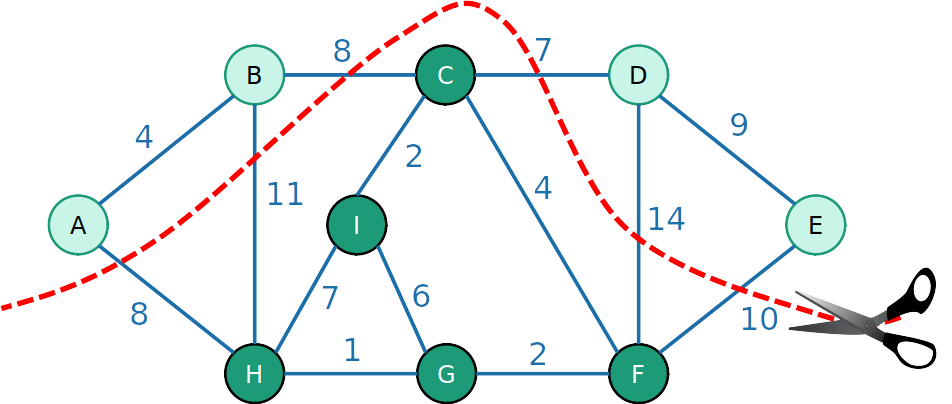
- Esse é o corte {A,B,D,E} e {C,I,H,G,F}
Corte
- Uma ou ambas das duas partes podem ser desconexas
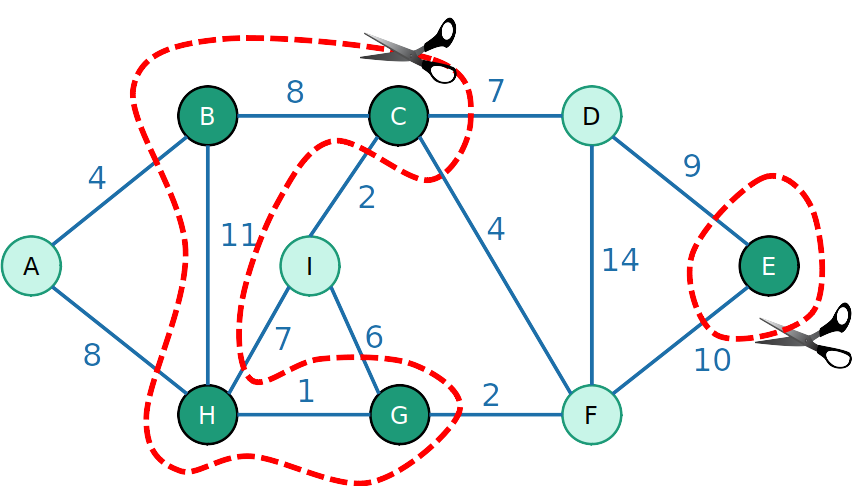
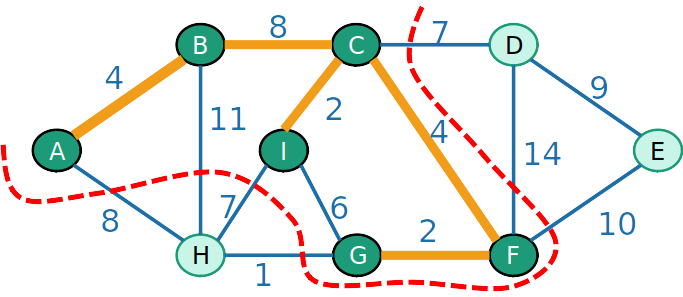
- Esse é o corte {A,I,D,F} e {B,C,E,H,G}
Corte
- Seja S um subconjunto dos nós de G
- Dizemos que o um corte respeita respeita S se nenhuma aresta de S cruza o corte
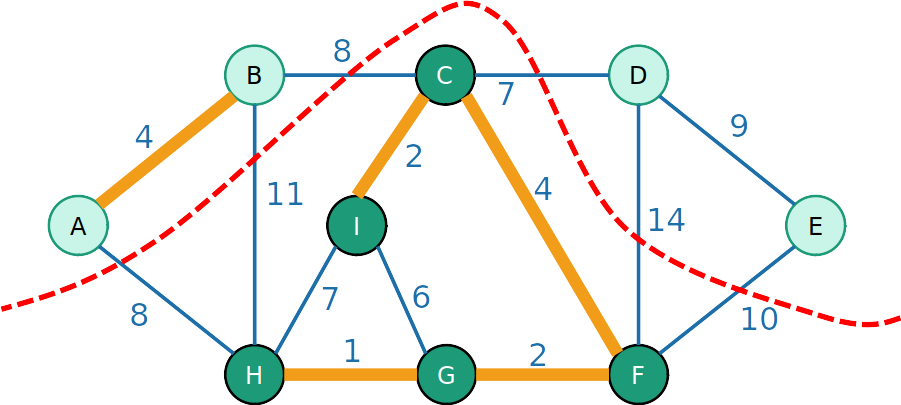
Corte
- A aresta de menor peso que que cruza o corte é chamada de aresta leve
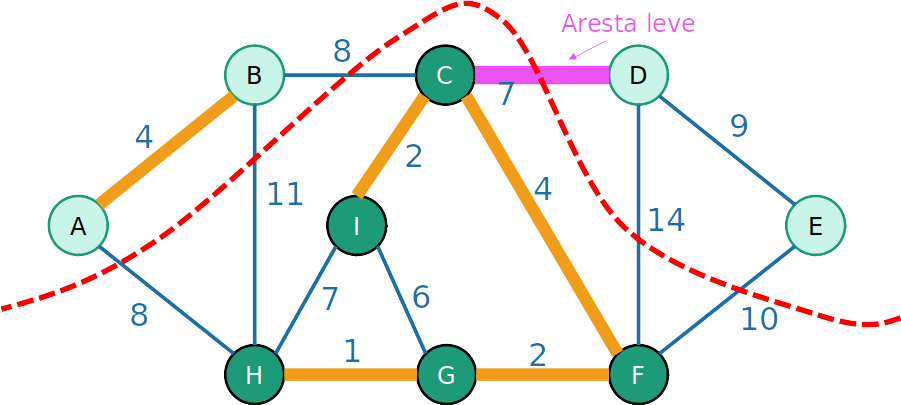
Aresta leve está na MST
- Seja S um conjunto de arestas e considere um corte que respeita S.
- Suponha que existe uma MST que contenha S
- Seja (u,v) uma aresta leve
- Então a MST conterá S∪{uv}
Aresta leve está na MST
- Suponha que temos:
- um corte que respeita S
- S é parte de alguma MST T
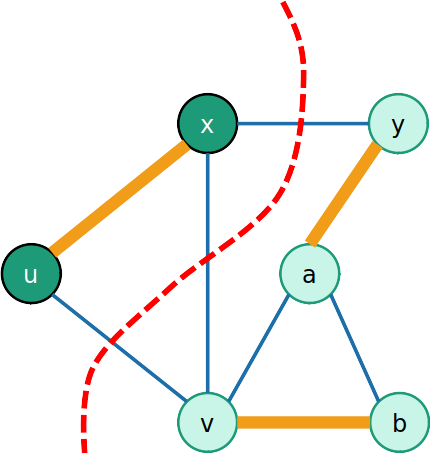
Aresta leve está na MST
-
Suponha que temos:
- um corte que respeita S
- S é parte de alguma MST T
-
Assuma que (u,v) é leve
- Menor custo cruzando o corte
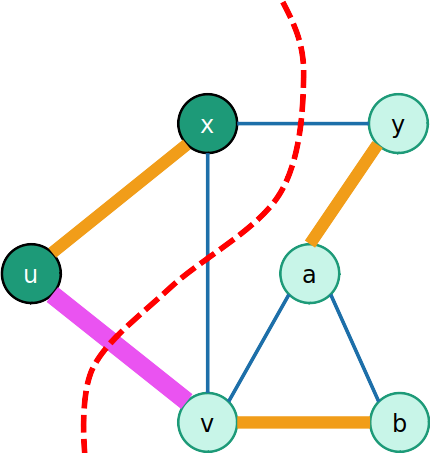
Aresta leve está na MST
-
Suponha que temos:
- um corte que respeita S
- S é parte de alguma MST T
-
Assuma que (u,v) é leve
- Menor custo cruzando o corte
-
Se (u,v)∈T, nenhuma outra aresta que cruza o corte pode estar em T
- Caso contrário teríamos um ciclo
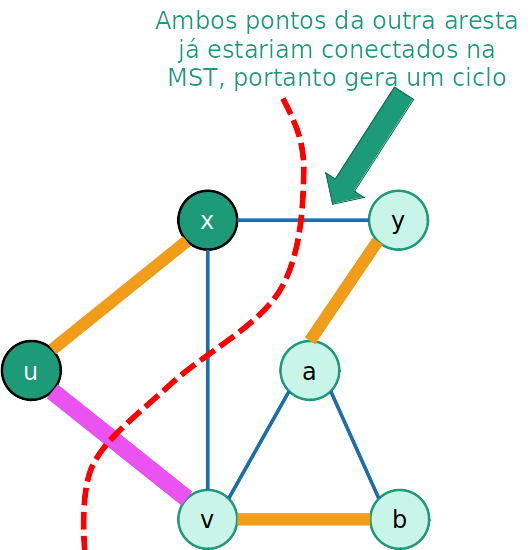
Aresta leve está na MST
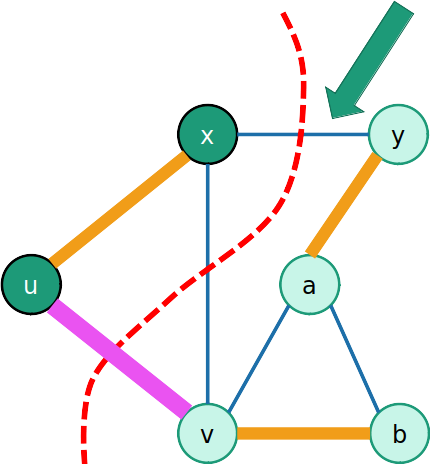
- Suponha que (u,v)∈/T. Existe portanto outra aresta (x,y) que cruza o corte que pertence a T.
- Seja T′ a MST obtida trocando (x,y) por (u,v)
w(T′)=w(T)−w(x,y)+w(u,v)
- Como w(u,v)≤w(x,y), ou seja:
w(T′)≤w(T)
- Portanto T não pode ser uma MST, pois a árvore que inclui a aresta leve tem um peso menor
Algoritmo de Prim
- Escolha uma raíz para a árvore e de maneira gulosa adiciona a aresta de menor peso que podemos para crescer essa árvore
Algoritmo de Prim
- Escolha uma raíz para a árvore e de maneira gulosa adiciona a aresta de menor peso que podemos para crescer essa árvore
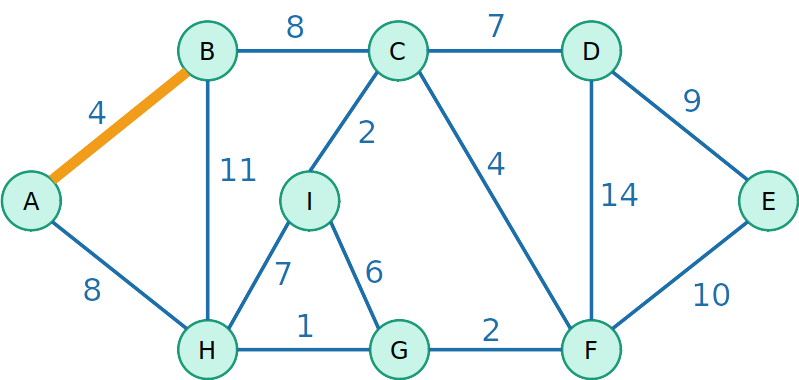
Algoritmo de Prim
- Escolha uma raíz para a árvore e de maneira gulosa adiciona a aresta de menor peso que podemos para crescer essa árvore
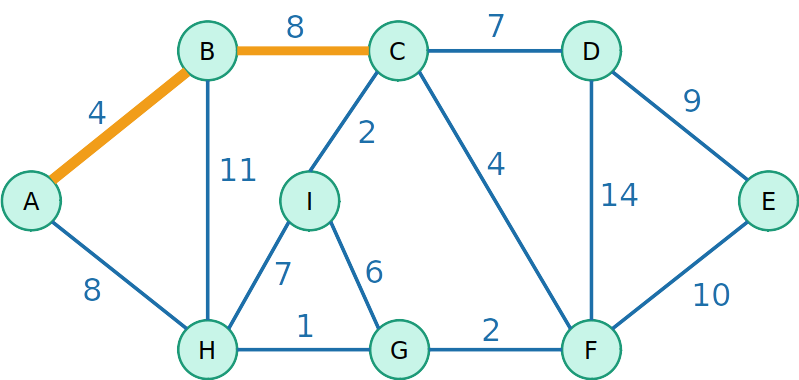
Algoritmo de Prim
- Escolha uma raíz para a árvore e de maneira gulosa adiciona a aresta de menor peso que podemos para crescer essa árvore
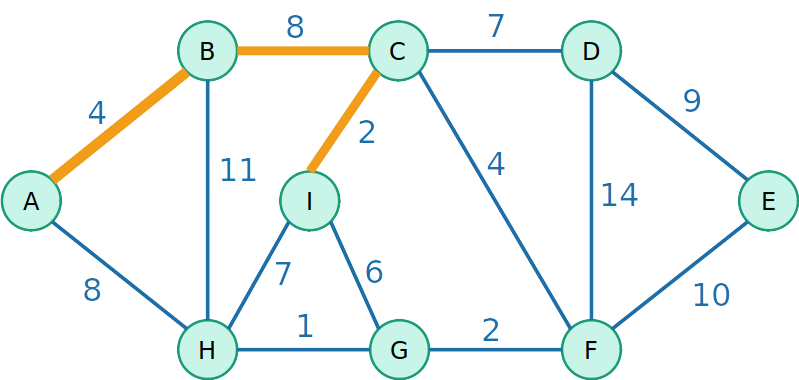
Algoritmo de Prim
- Escolha uma raíz para a árvore e de maneira gulosa adiciona a aresta de menor peso que podemos para crescer essa árvore
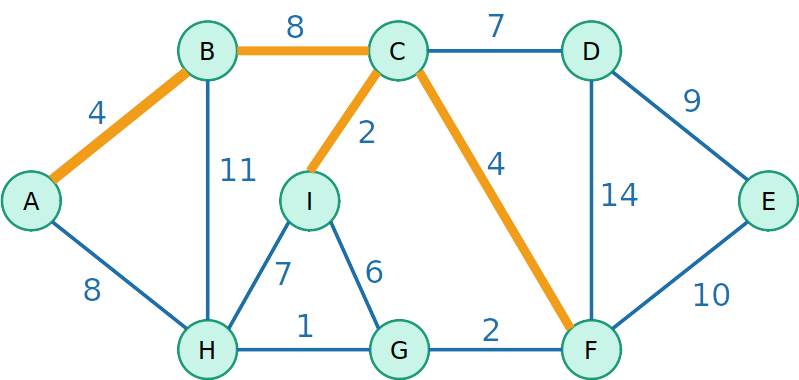
Algoritmo de Prim
- Escolha uma raíz para a árvore e de maneira gulosa adiciona a aresta de menor peso que podemos para crescer essa árvore
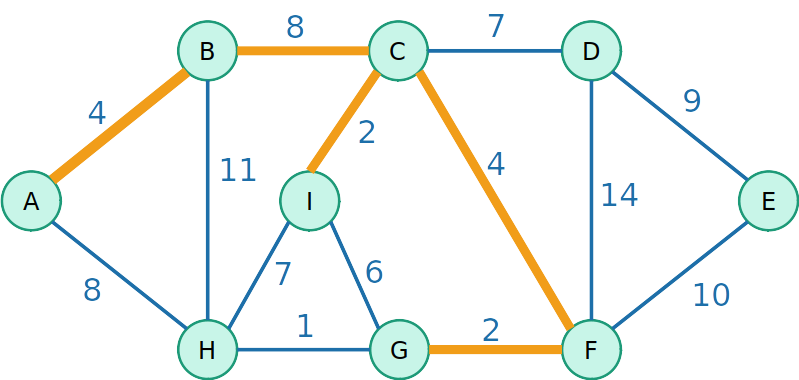
Algoritmo de Prim
- Escolha uma raíz para a árvore e de maneira gulosa adiciona a aresta de menor peso que podemos para crescer essa árvore
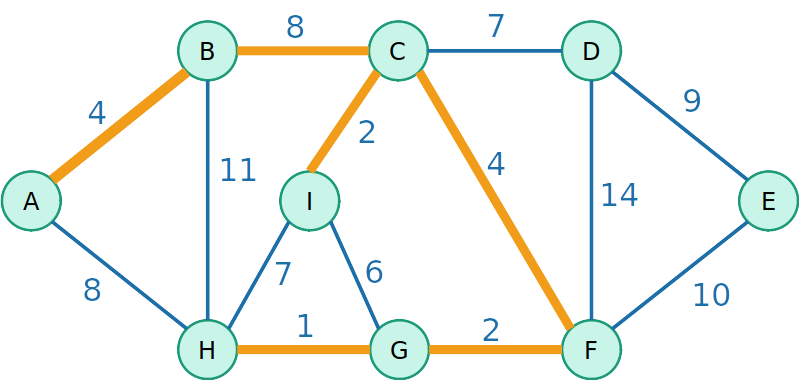
Algoritmo de Prim
- Escolha uma raíz para a árvore e de maneira gulosa adiciona a aresta de menor peso que podemos para crescer essa árvore
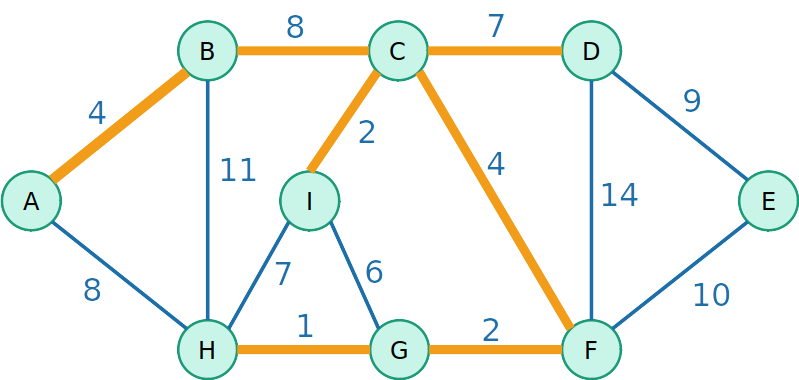
Algoritmo de Prim
- Escolha uma raíz para a árvore e de maneira gulosa adiciona a aresta de menor peso que podemos para crescer essa árvore
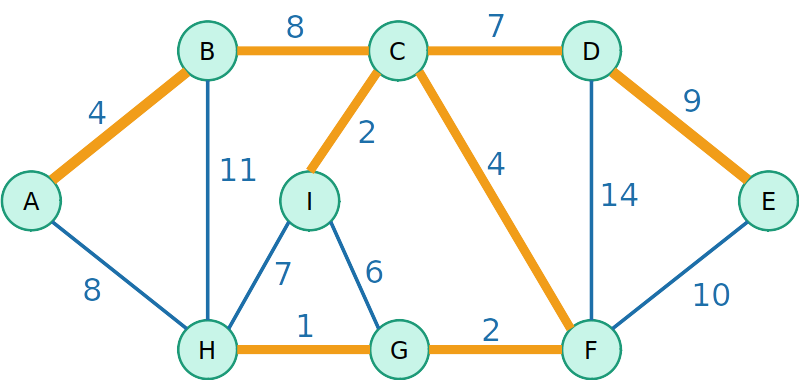
Algoritmo de Prim

Por que funciona?
- Considere a MST atual
- E considere o corte {visitados, não visitados}
Por que funciona?
- Considere a MST atual,
- E considere o corte {visitados, não visitados}
- O conjunto S de arestas selecionadas até agora respeita o corte
- A aresta adicionada é uma aresta leve
- Pelo lema, ela é uma aresta segura para adicionar
Por que funciona?
- A estratégia gulosa não exclui uma solução ótima
- Por indução, podemos provar que a corretudo do algoritmo de Prim
Qual a complexidade?
- O algoritmo adiciona um vértice de cada vez, portanto o laço da linha 3 executa Θ(m), em que m=∣V(G)∣
- Para encontrar a aresta leve, podemos fazer uma busca sobre todas as arestas, e verificar se ela cruza o corte, armazenando a de menor peso. Essa estratégia custa Θ(n), em que n=∣E(G)∣
- Portanto, a complexidade dessa estratégia é Θ(nm).
Dá pra fazer melhor?
- Para diminuir a complexidade, podemos usar uma estratégia diferente para encontrar a aresta leve
- Podemos fazer isso usando uma Heap para selecionar a aresta leve que adiciona um nó não visitado na árvore
PrimHeap
-
Cada nó deve armazenar:
- O distância até o nó mais próximo da árvore MST
- Qual é o nó mais próximo
-
Se ainda não sabemos qual é a distância, ela é inicializada como infinito
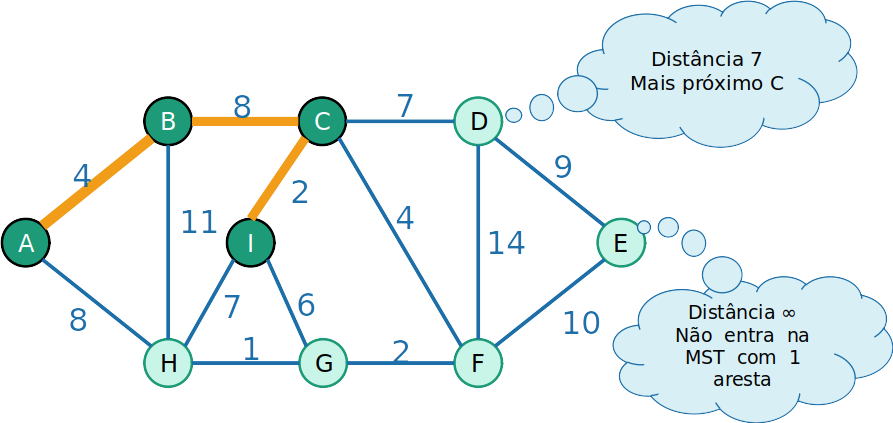
PrimHeap
-
Cada nó deve armazenar:
- O distância até o nó mais próximo da árvore MST
- Qual é o nó mais próximo
-
Quando uma nova aresta é adiciona na árvore, atulizamos as informações
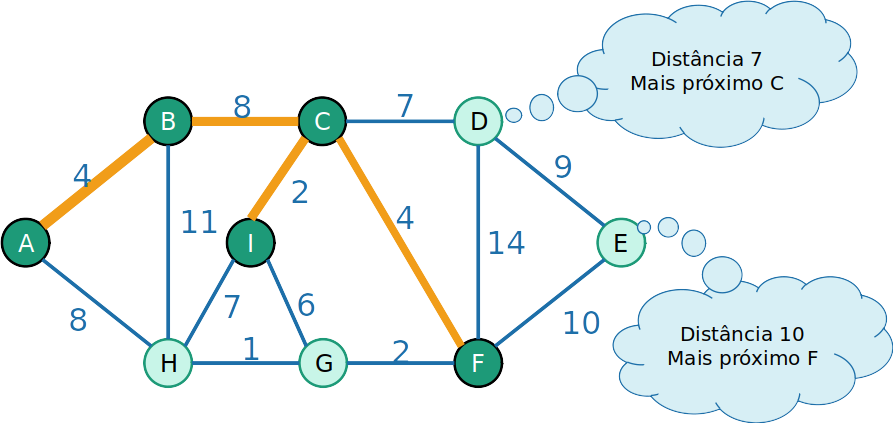
PrimHeap
- Iniciando a construção da MST a partir do nó A
- Para os vizinhos v de A, o prodedessor de v é A, e a prioridade é −w(e), em que e é a aresta de A a v
- Para os não vizinhos de A, a prioridade é −∞
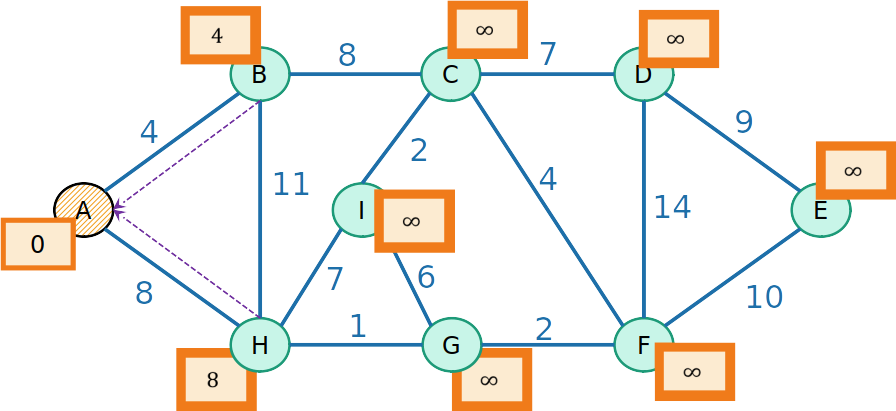
PrimHeap
- A é inserido na MST
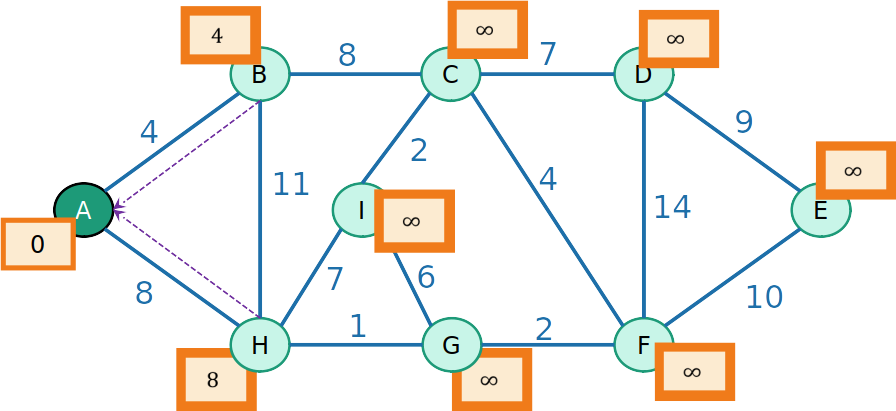
PrimHeap
- Retiramos da Heap o nó de maior prioridade, que é B
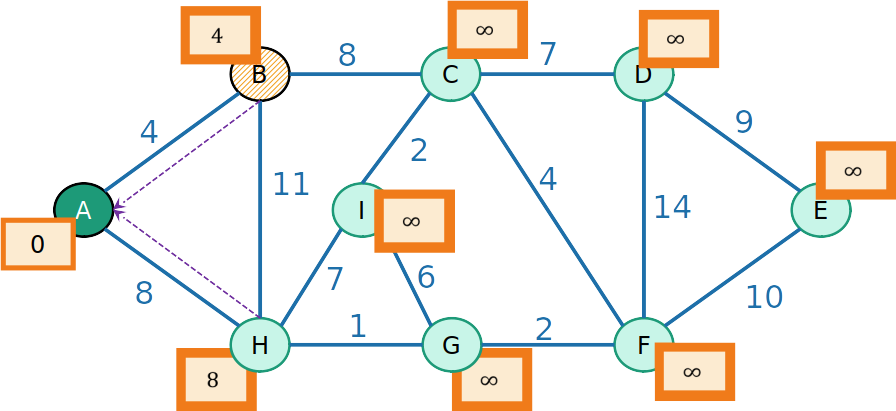
PrimHeap
- Para os vizinhos v de B, o prodedessor de v é B, e a prioridade é atualizada para −w(e), em que e é a aresta de B a v
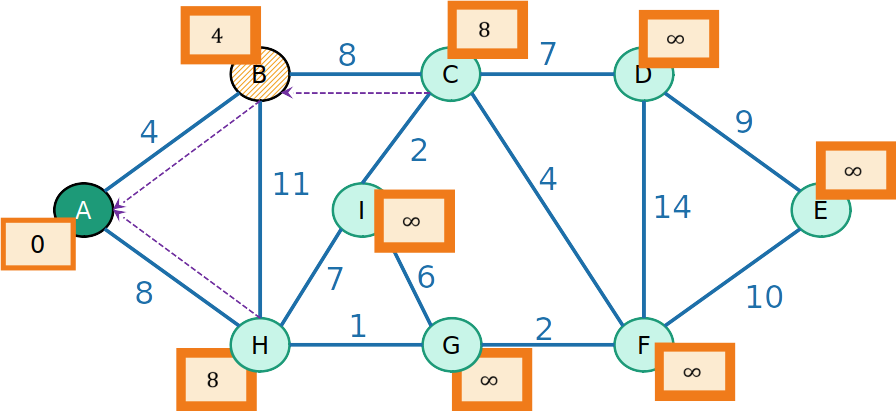
PrimHeap
- Como o prodedessor de B é A, o vértice B e a aresta (A,B) são inseridos na MST
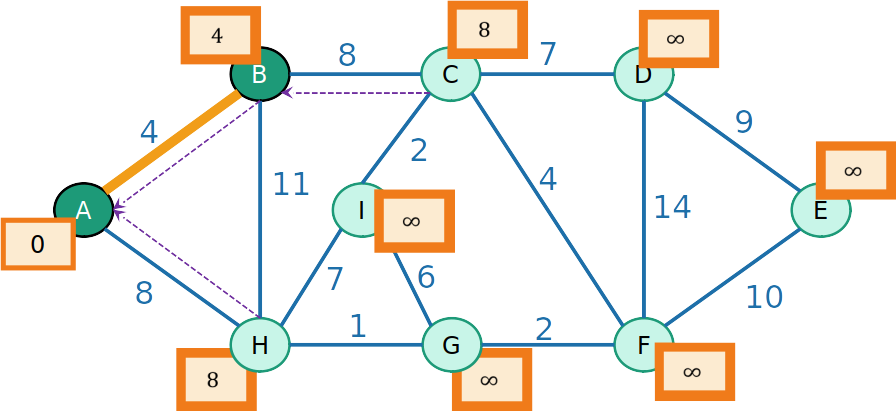
PrimHeap
- Retiramos da Heap o nó de maior prioridade, que é C (nesse caso, empatado com H)
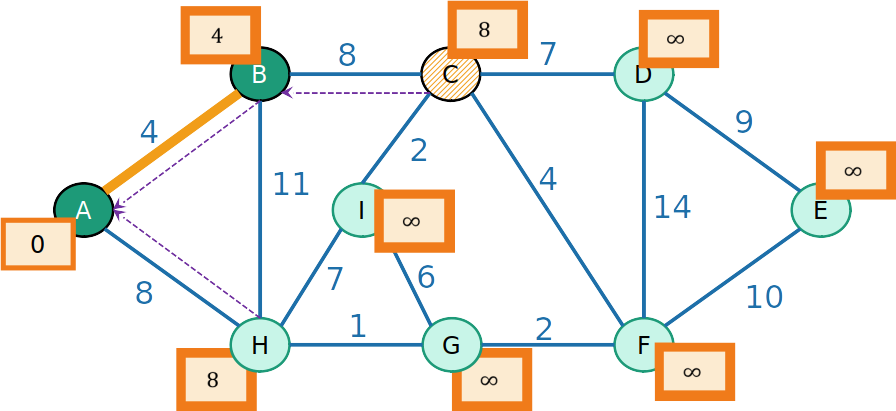
PrimHeap
- Para os vizinhos v de C, o prodedessor de v é C, e a prioridade é atualizada para −w(e), em que e é a aresta de C a v
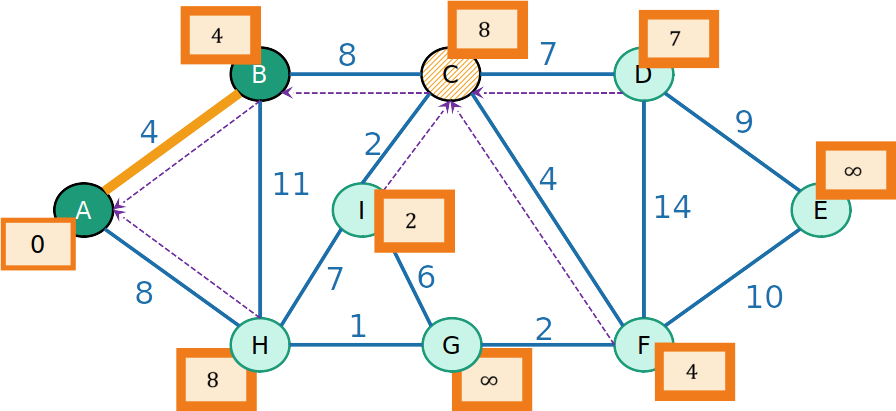
PrimHeap
- Como o prodedessor de C é B, o vértice B e a aresta (A,B) são inseridos na MST
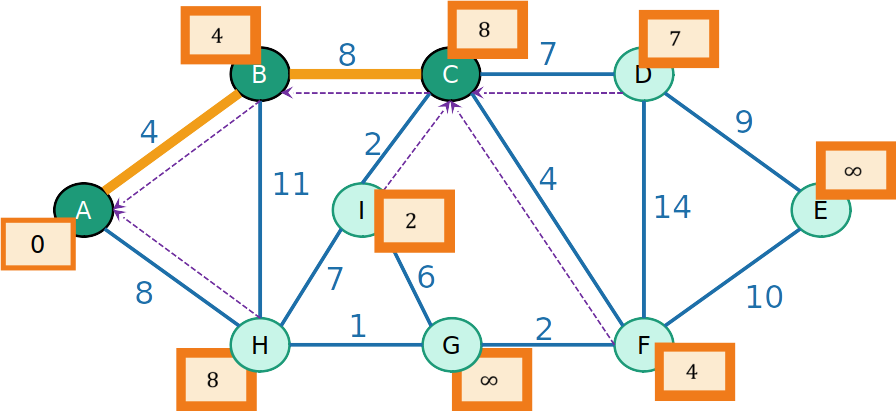
PrimHeap
- Retiramos da Heap o nó de maior prioridade, que é I
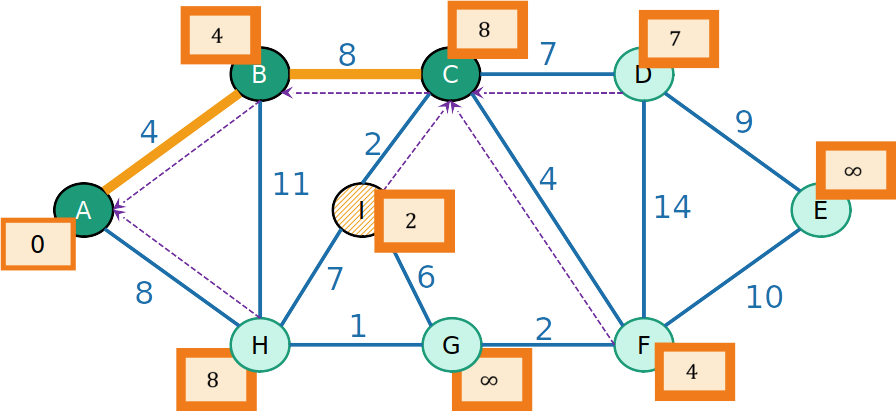
PrimHeap
- Para os vizinhos v de I, o prodedessor de v é I, e a prioridade é atualizada para −w(e), em que e é a aresta de C a v
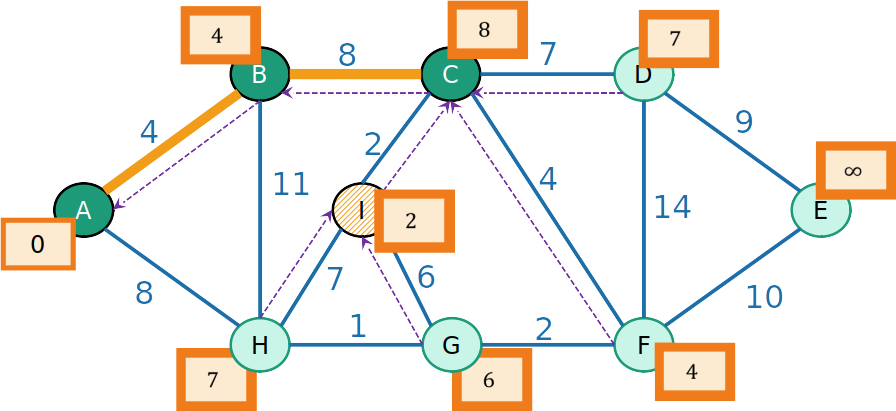
PrimHeap
- Como o prodedessor de I é C, o vértice I e a aresta (C,I) são inseridos na MST
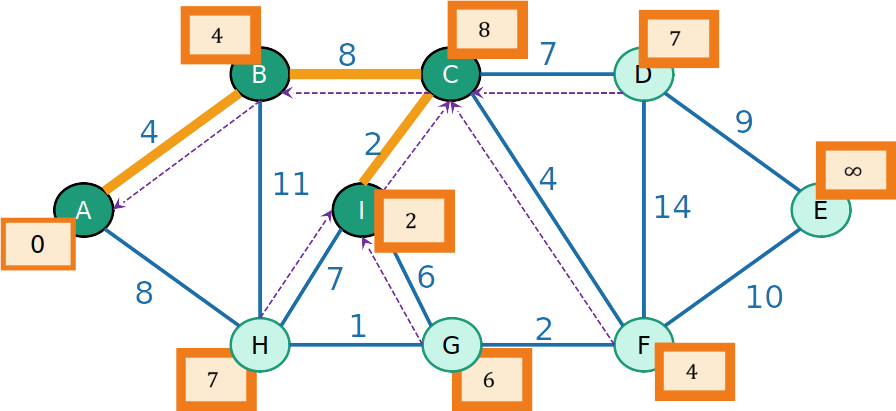
PrimHeap
- Retiramos da Heap o nó de maior prioridade, que é F
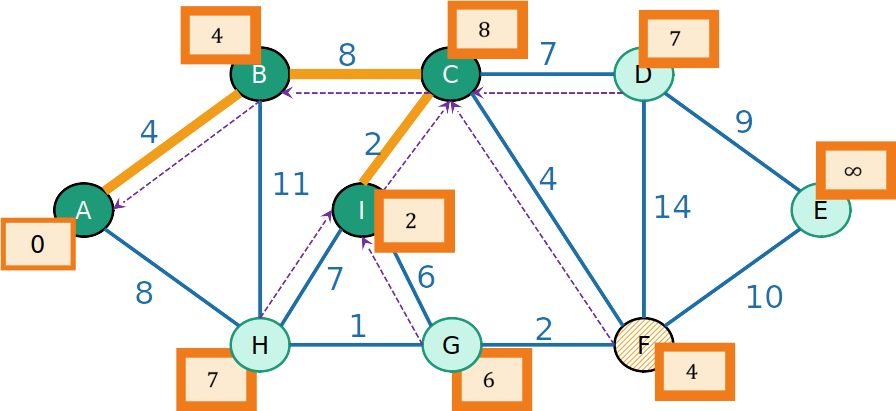
PrimHeap
- Para os vizinhos v de F, o prodedessor de v é F, e a prioridade é atualizada para −w(e), em que e é a aresta de F a v
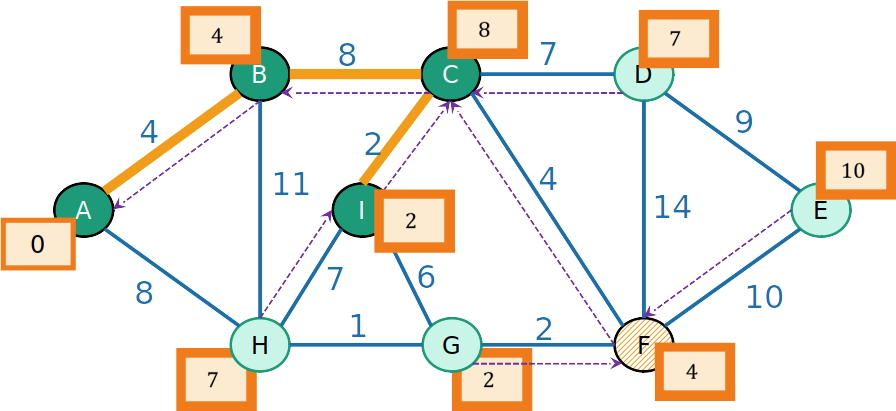
PrimHeap
- Como o prodedessor de I é C, o vértice I e a aresta (C,I) são inseridos na MST
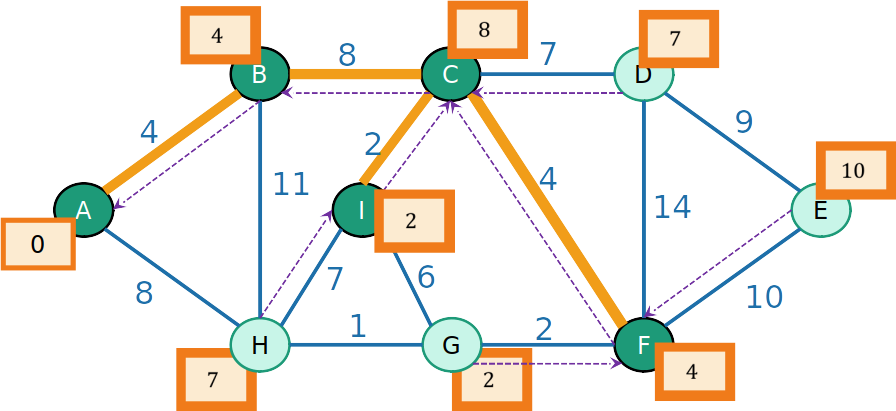
PrimHeap
- E continuamos o processo até construir toda a MST
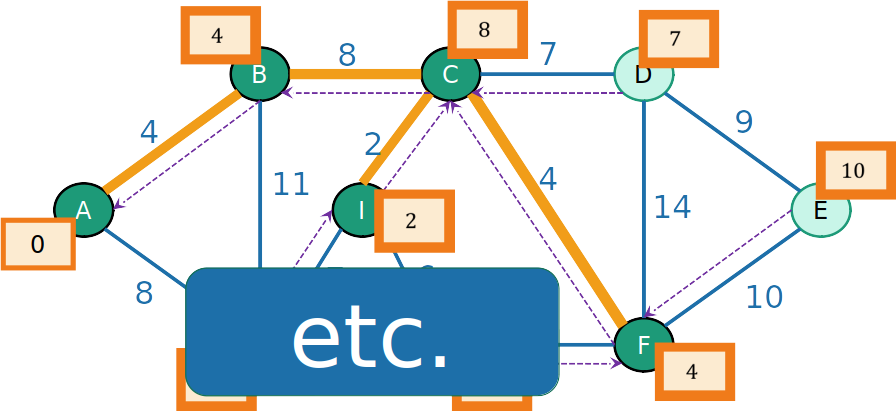
PrimHeap

PrimHeap - Complexidade
- Seja n=∣V(G)∣ e m=E(G).
- Fazemos O(n) remoções da heap, com um tempo total O(nlogn)
- O total de alterações é O(m), com um tempo total O(mlogn).
- Assim, o tempo total do algoritmo é O(mlogn).
Kruskal
- Vamos testar agora uma outra estratégia gulosa de inserir a aresta de menor custo
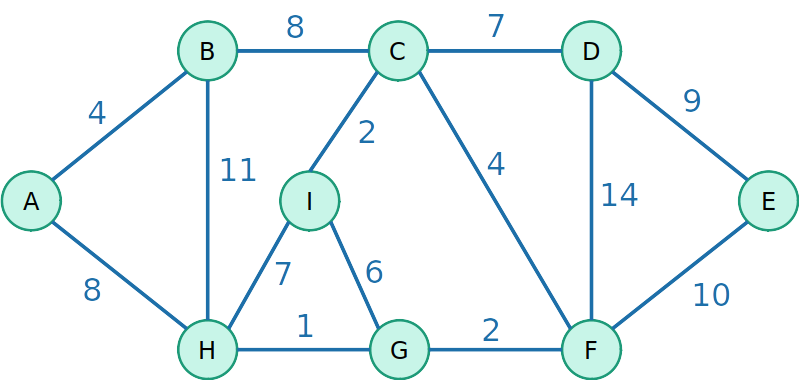
Kruskal
- Vamos testar agora uma outra estratégia gulosa de inserir a aresta de menor custo
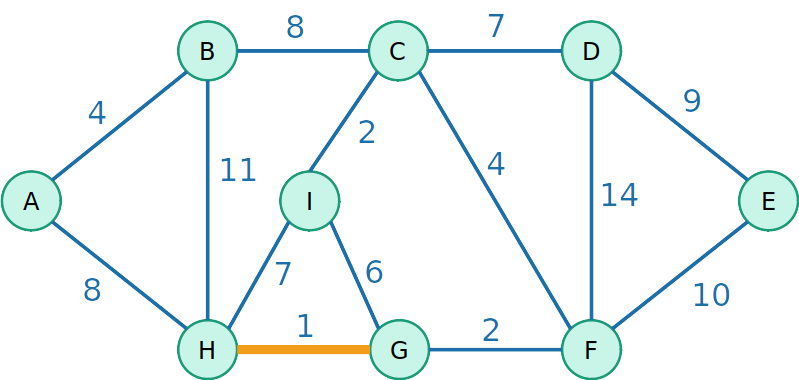
Kruskal
- Vamos testar agora uma outra estratégia gulosa de inserir a aresta de menor custo
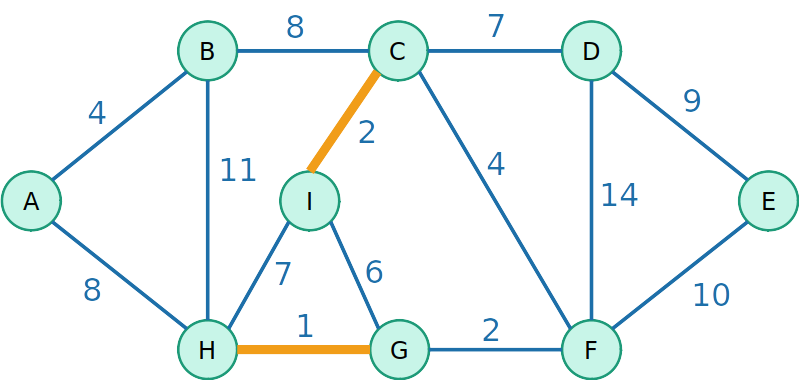
Kruskal
- Vamos testar agora uma outra estratégia gulosa de inserir a aresta de menor custo
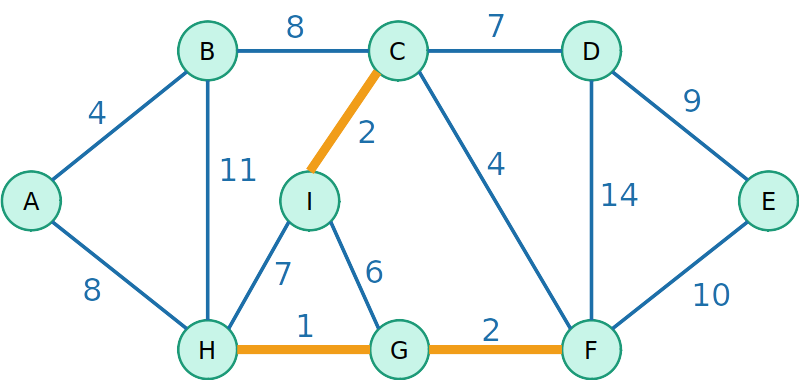
Kruskal
- Vamos testar agora uma outra estratégia gulosa de inserir a aresta de menor custo
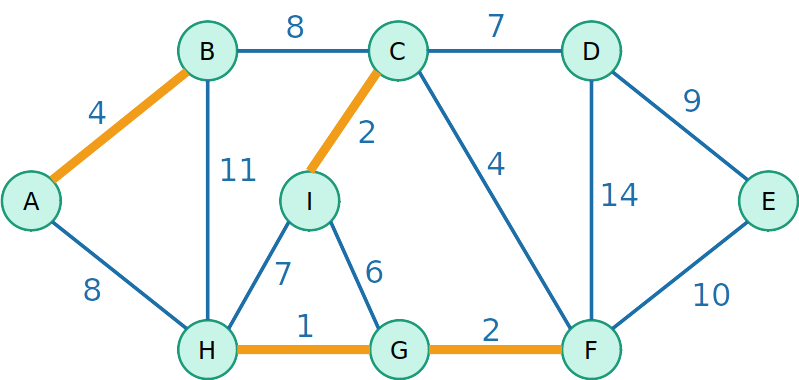
Kruskal
- Vamos testar agora uma outra estratégia gulosa de inserir a aresta de menor custo
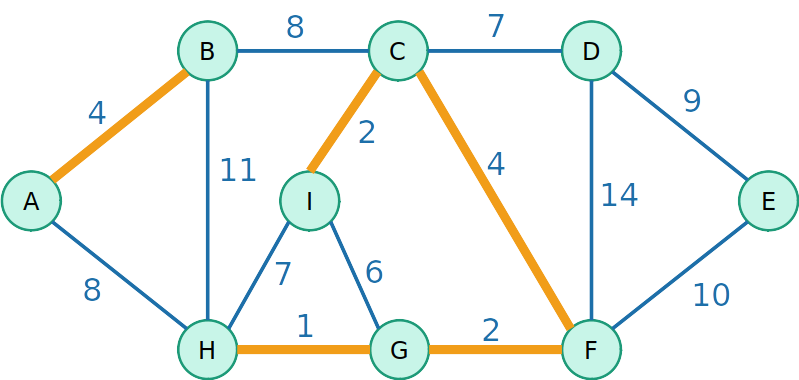
Kruskal
- Vamos testar agora uma outra estratégia gulosa de inserir a aresta de menor custo
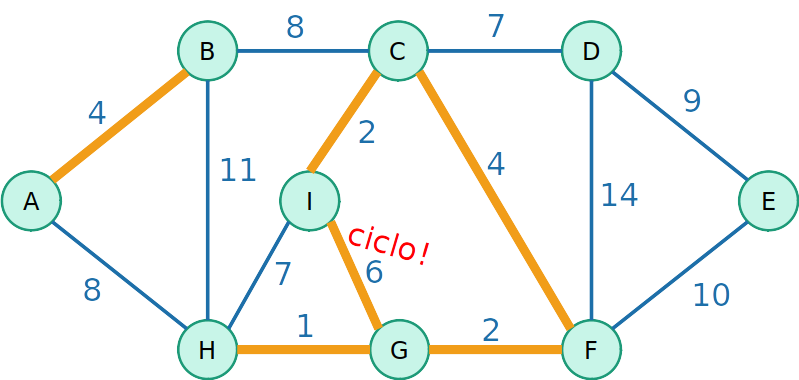
Kruskal
- A estratégia gulosa de inserir a aresta de menor custo pode levar ao aparecimento de ciclos
- Precisamos de uma estratégia gulosa de inserir a aresta de menor custo e que não gera ciclos
Kruskal
- Vamos testar agora uma outra estratégia gulosa de inserir a aresta de menor custo
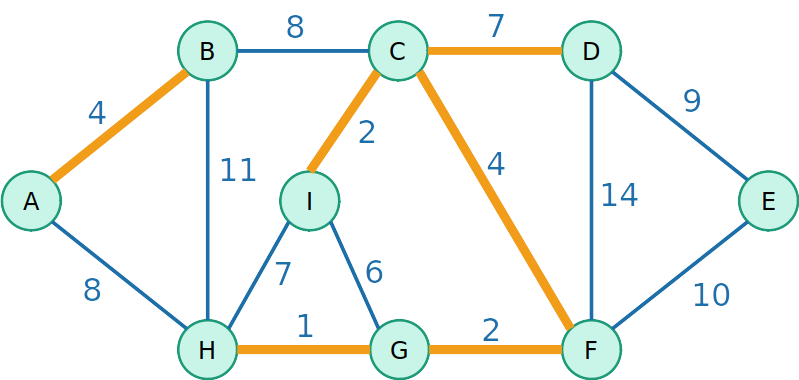
Kruskal
- Vamos testar agora uma outra estratégia gulosa de inserir a aresta de menor custo
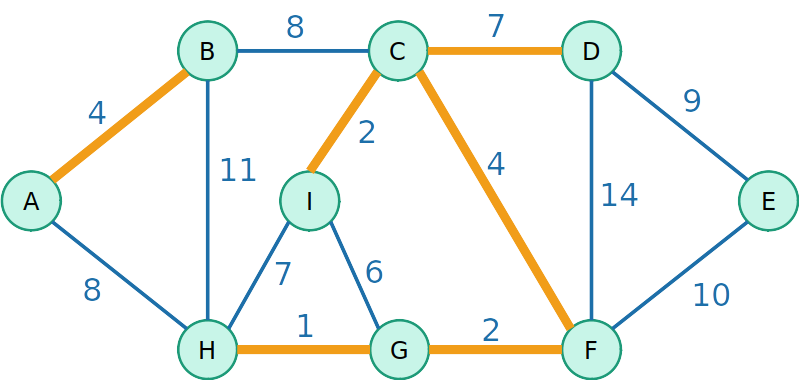
Kruskal
- Vamos testar agora uma outra estratégia gulosa de inserir a aresta de menor custo
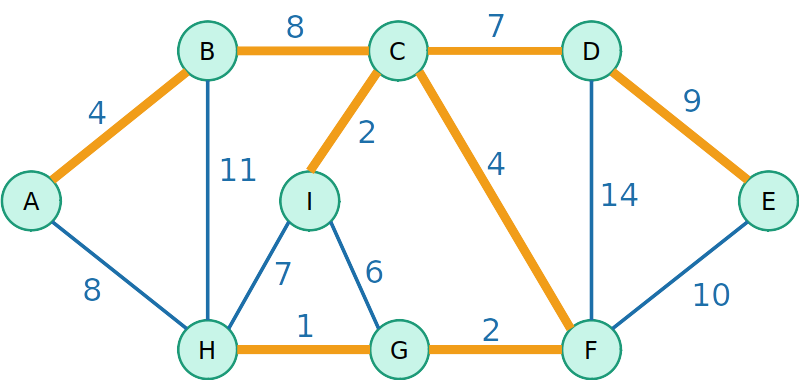
Kruskal

Kruskal
- A cada iteração do algoritmo de Kruskal, estamos mantendo uma floresta (uma coleção de árvores desconexas)
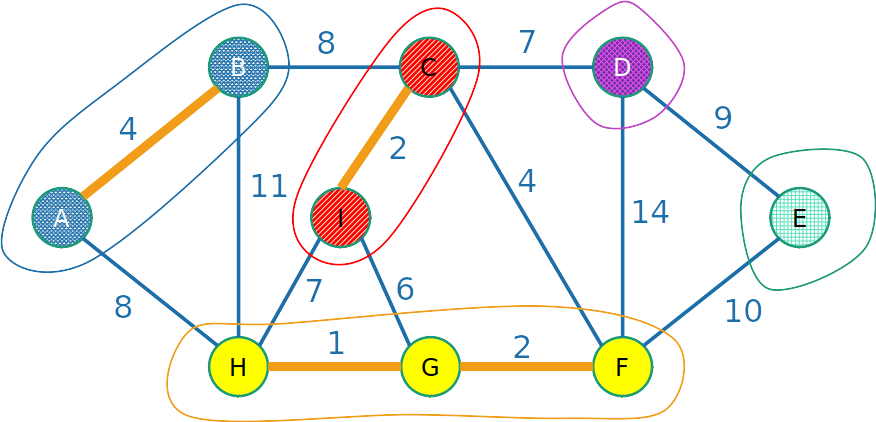
Kruskal
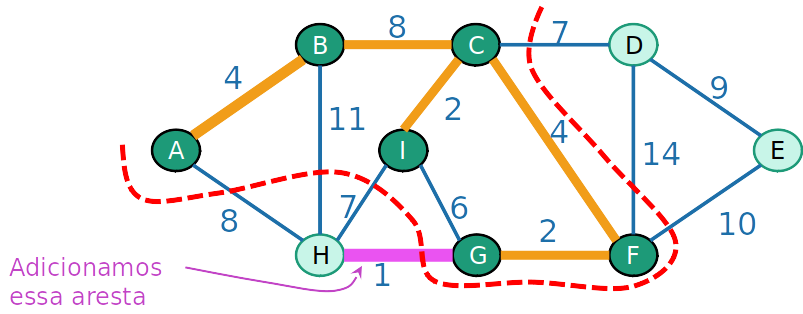
- Quando adicionamos uma aresta, juntamos duas árvores
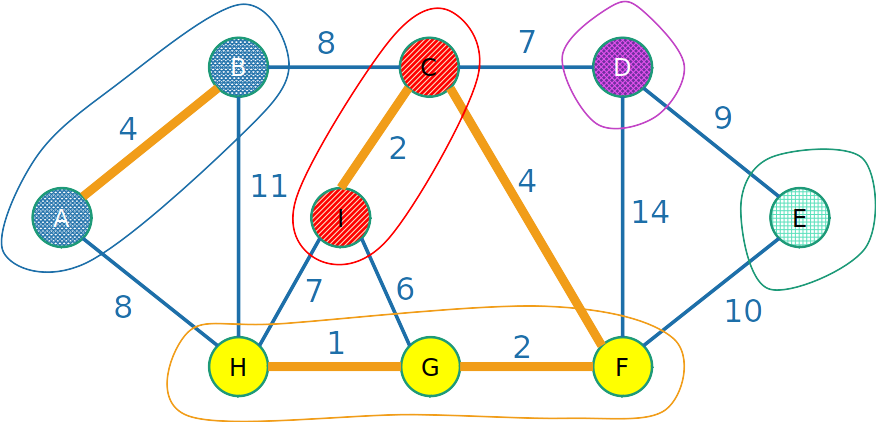
Kruskal
- Nunca adicionamos uma aresta dentro de uma árvore, senão criaríamos um ciclo
Qual a complexidade?
- Seja m=∣V(G)∣, e n=∣V(E)∣
- O algoritmo adiciona um vértice de cada vez, portanto o laço da linha 3 executa m vezes
- Utilizando um algoritmo de busca para detectar ciclos, ele executa em O(n+∣F∣), em que F é o número de vértices já inseridos na MST
- A MST tem no máximo n−1 vértices, portanto a busca é feita em O(n)
- Utilizando essa estratégia, o algoritmo executa em O(nm)
Dá pra fazer melhor?
- Para diminuir a complexidade, podemos usar uma estratégia diferente para encontrar ciclos
- Podemos fazer isso usamos uma estrutura de dados que dá suporte à criação, busca e união de conjuntos
UnionFind
- Estrutua de dados que dá suporte as seguintes operações:
- makeSet(u): cria o conjunto {u}
- find(u): retorna o conjunto que u pertence
- union(u,v): faz a unição dos conjuntos em que u e v pertencem
UnionFind
makeSet(x)
makeSet(y)
makeSet(z)
UnionFind
makeSet(x)
makeSet(y)
makeSet(z)
union(x,y)
UnionFind
makeSet(x)
makeSet(y)
makeSet(z)
union(x,y)
find(x)
UnionFind
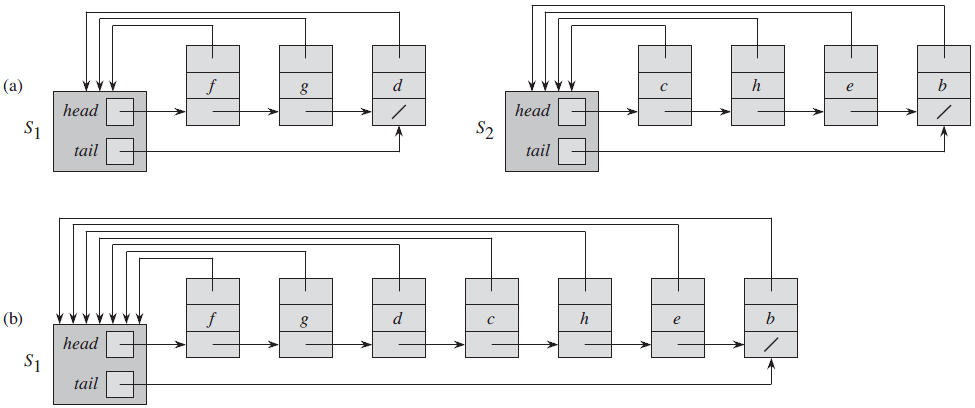
-
Conjuntos pedem ser representados por listas encadeadas.
-
Cada elemento tem um representante, que é a cabeça da lista
- Consultar a qual conjunto um elemento pertence é feita em O(1), pois simplesmente retornamos quem é o seu representante
-
Na união de dois conjuntos, fazemos a cauda de uma das listas apontar para cabeça da outra (unindo as duas listas)
- Tem complexidade min(∣L1∣,∣L2∣)
UnionFind


UnionFind

UnionFind
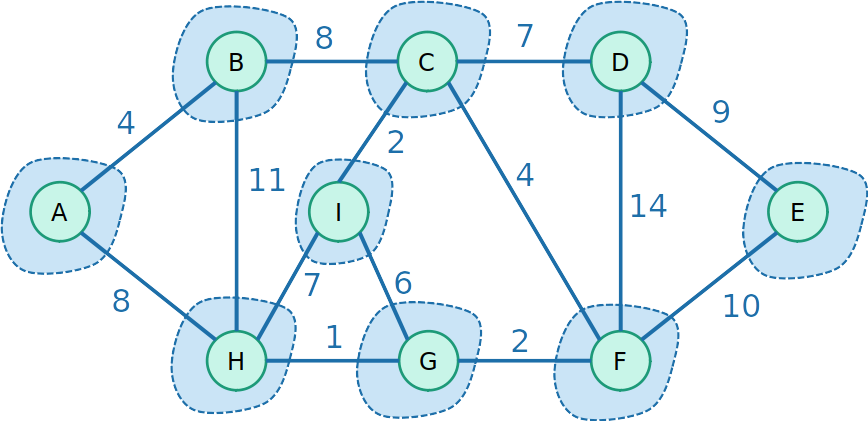
Kruskal com Union-Find
- Inicialmente, cada vértice é a sua própria árvore, e cada conjunto tem um vértice
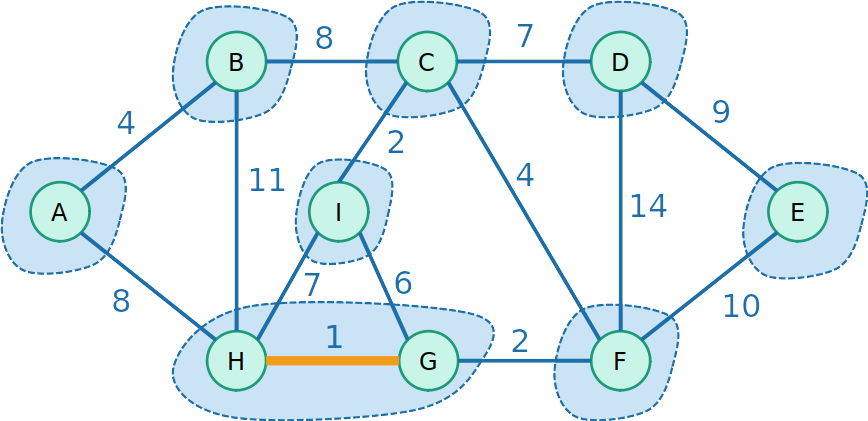
Kruskal com Union-Find
- Então começamos a unir os conjuntos
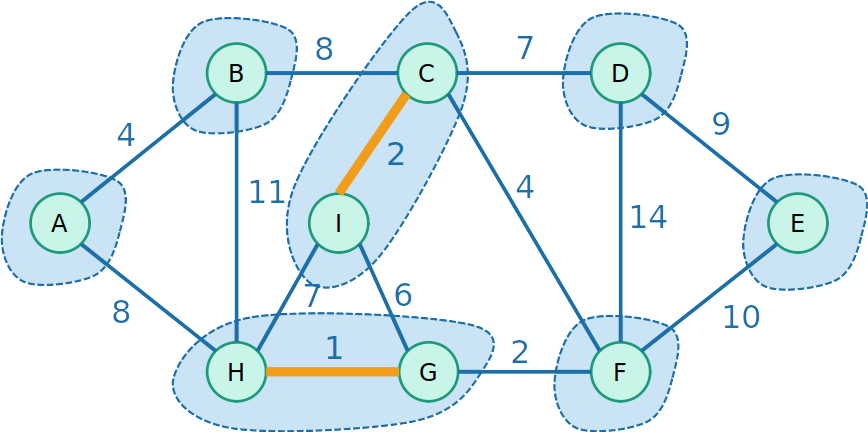
Kruskal com Union-Find
- Então começamos a unir os conjuntos
Kruskal com Union-Find
- Então começamos a unir os conjuntos
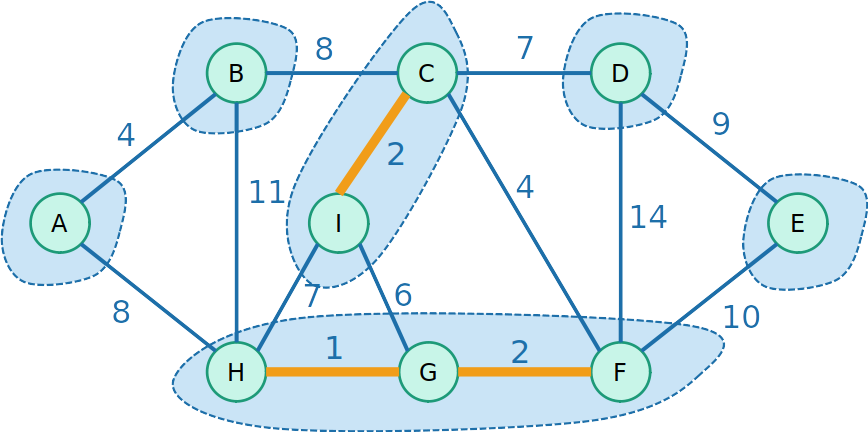
Kruskal com Union-Find
- Então começamos a unir os conjuntos
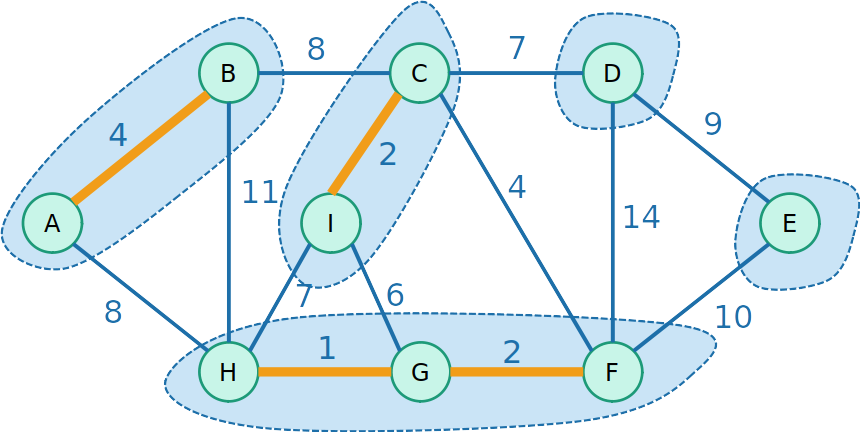
Kruskal com Union-Find
- Então começamos a unir os conjuntos
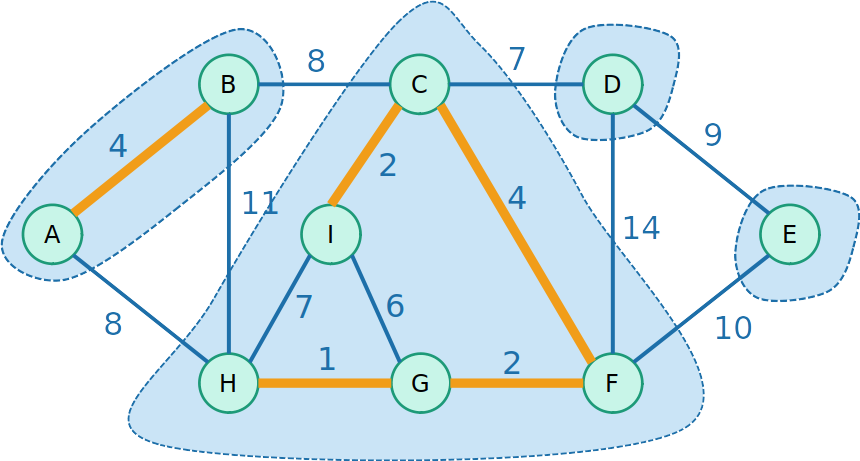
Kruskal com Union-Find
- Então começamos a unir os conjuntos
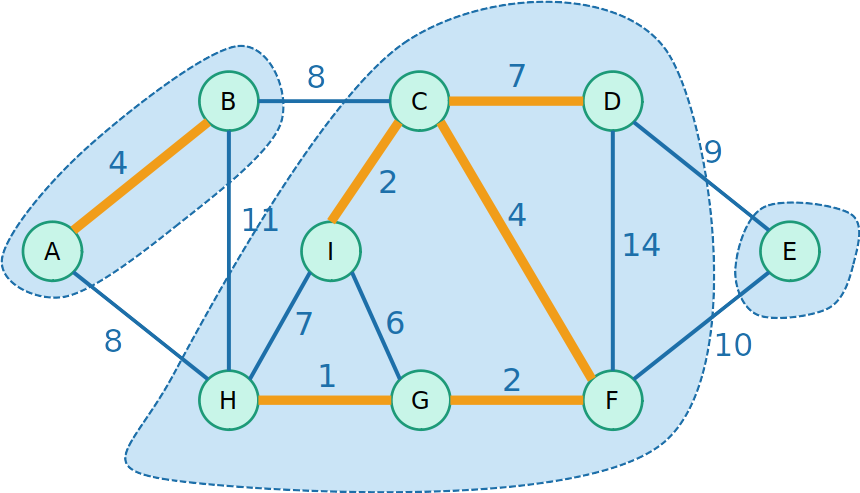
Kruskal com Union-Find
- Então começamos a unir os conjuntos
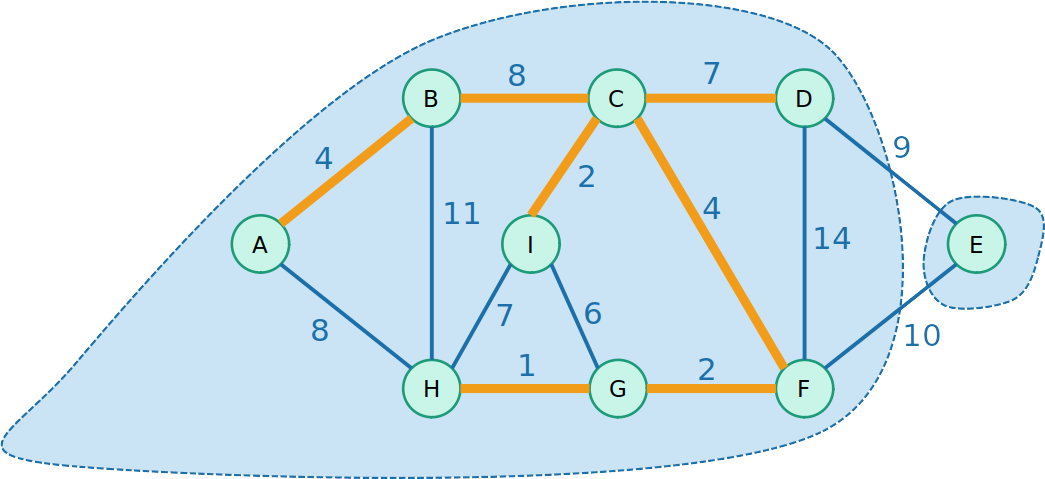
Kruskal com Union-Find
- Até incluir todos os nós
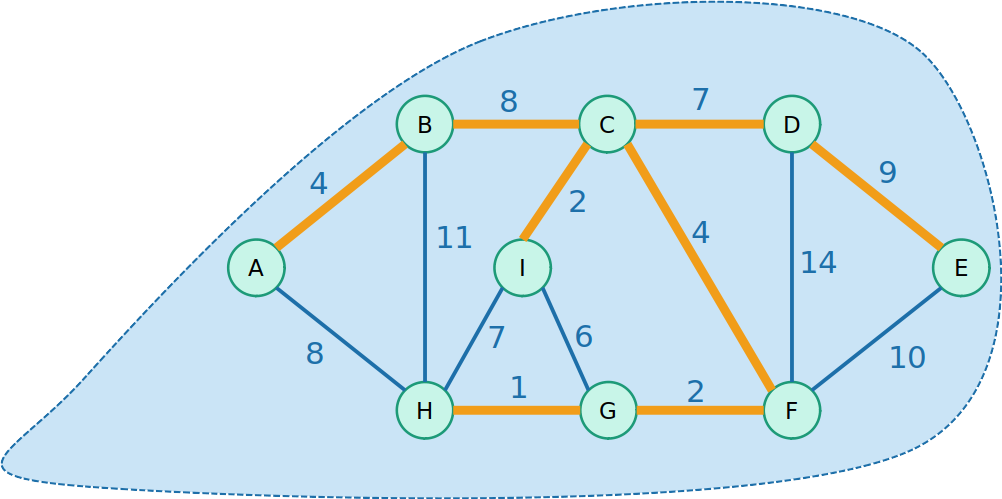
Funciona?
- Cosidere a próxima aresta que iremos incluir
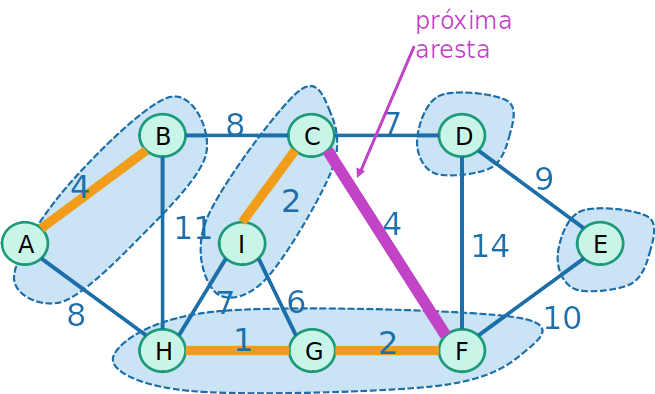
- Essa operação irá unir duas árvores, representadas por dois conjuntos de arestas T1 e T2
Funciona?
- Considere o corte formato por {T1,V−T1}
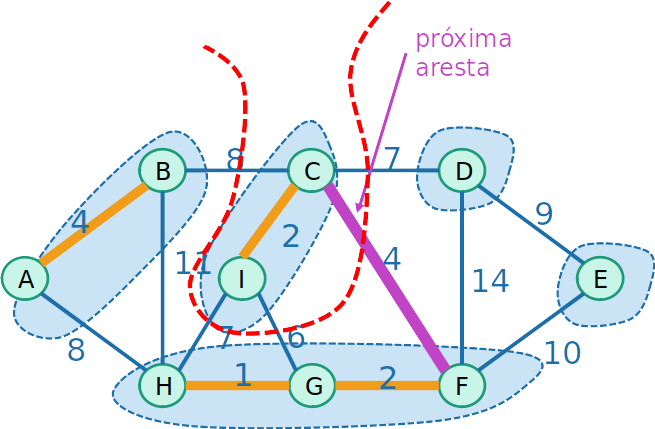
- A próxima aresta é uma aresta leve, e portanto segura de ser inserida
- Usando essa propriedade, é possível provar por indução que o algoritmo funciona.
Kruskal com Union-Find

Qual é a complexidade?
- Seja n=∣V(G)∣ e m=E(G).
- O laço da linha 6 executa O(m) vezes
- Dentro do laço, a etapa mais custosa é a união de dois conjuntos.
- Quando unimos dois conjuntos, a operação mais custosa é atualizar o representante do menor deles.
- Entretanto, o menor deles pelo menos dobra de tamanho.
- O número de atualizações é, portanto, O(logn)
- Portanto a complexidade do algoritmo é O(mlogn)
Comparação
-
Prim:
- cresce uma árvore
- complexidade é O(mlogn) com uma heap
-
Kruskal:
- cresce uma floresta
- complexidade é O(mlogn) com union find
-
Ambos são gulosos
- Subestrutura ótima: subgrafos gerados por cortes
- A maneira de fazer escolhas seguras (que não excluem uma solução ótima) é escolher arestas leves