Representação textual

• Caracteres são representados computacionalmente usando o código ascii out utf

• Número fixo de bits por caracter

• Mapeamento um para um de caracter para um conjunto de bits

• Total de bits = número de caracteres $\times$ bits por caracter

Representação textual

• Linguas no entanto tem um predominância do uso de alguns caracteres

• Ao contrário de "textos aleatórios", em que a distribuição é uniforme

Representação textual

• Suponha que temos alguma distribuição a respeito do uso de caracteres

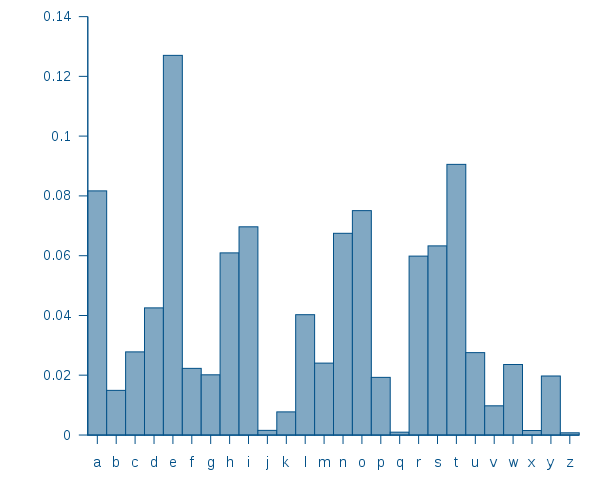
Representação textual

• Sem perda de generalidade, considere um alfabeto de 6 letras
• Como podemos codificar de maneira eficiente e não ambígua esses caracteres?

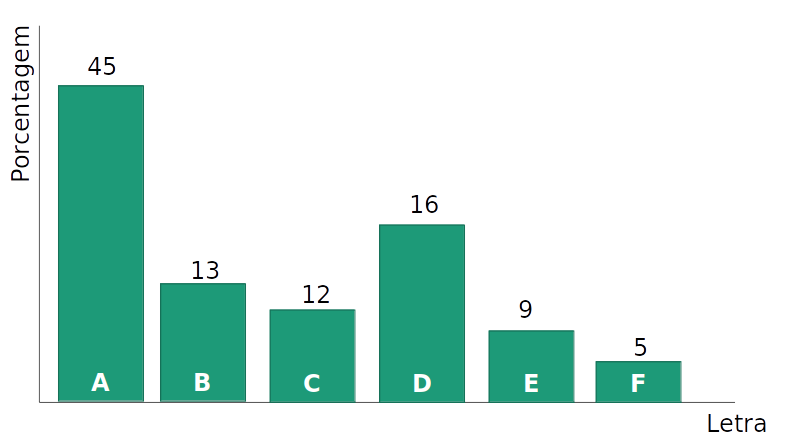
Representação textual

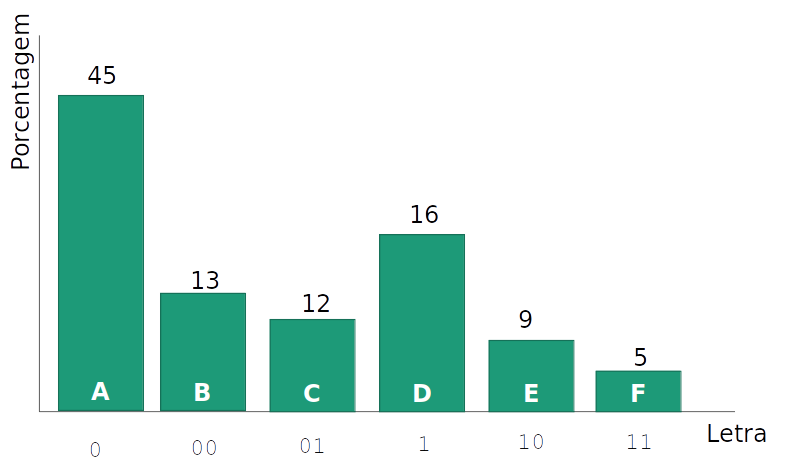
• Tentativa 1: Usando um número fixo de bits por caracter, os códigos 110 e 111 nunca são usados
• Uma representação compacta de 'A' economizaria espaço

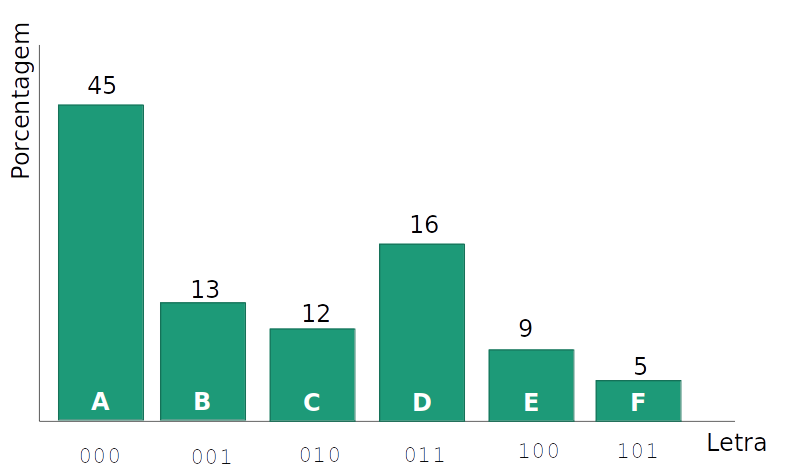
Representação textual

• Tentativa 2: Usando um número variável por caracter, em que as letras mais frequentes usam uma codificação menor, podemos ter ambiguidade
• OOO significa 'AAA' ou 'AB' ?

Representação textual

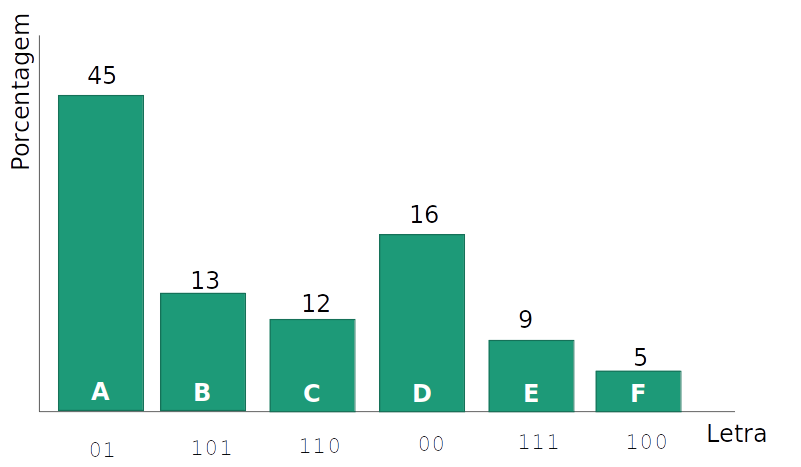
• Tentativa 3: Usando um número variável por caracter, em que as letras mais frequentes usam uma codificação menor, mas que nenhum código seja o prefixo de outro.
  • Tente decodificar 10010101

Representação livre de prefixo

• Qual é a maneira mais eficiente de criar uma códificação livre de prefixos?

• Como podemos usar o menor número possível de bits, sem criar um código ambíguo?

Árvore de prefixo

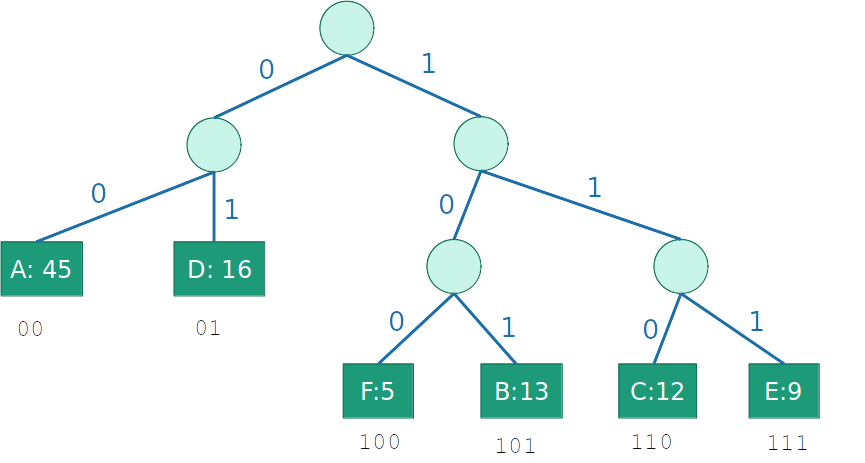
• Um código livre de prefixo pode ser represetado por uma árvore binária
  • As letras aparecem nas folhas
  • Uma ramificação à esquerda significa um '0', e a direita um '1'
  • O código para uma letra é a concatenação dos bits da raíz a folha

Quão boa é a árvore?

• Suponha que selecionamos uma letra aleatóriamente a partir de uma língua.

  • A probabilidade não é uniforme, ela segue a distribuição (o histograma)

• O custo da árvore é o tamanho esperado da codificação daquela letra

$C(T) = \sum_{x\in folhas(T)} P(x)\cdot d_T(x)$

• Em que $d_T(x)$ é a distância da raíz até a folha (altura) do caracter 'x'
• No nosso exemplo:

$C = 2(0,45 + 0,16) + 3(0,05 + 0,13 + 0,12 + 0,09) = 2,39$

Problema

• Dada uma distribuição $P(x)$ sobre um conjunto de caracteres, como encontrar a árvore de custo mínimo?

$C(T)_{minimo} = \min \sum_{x\in folhas(T)} P(x)\cdot d_T(x)$

Estratégia gulosa

• Gulosamente construir sub-árvores de baixo para cima
• Objetivo guloso: letras menos frequentes devem aparecer mais abaixo na árvore

Codificação de Huffman

• Gulosamente construir sub-árvores de baixo para cima

Codificação de Huffman

• Gulosamente construir sub-árvores de baixo para cima

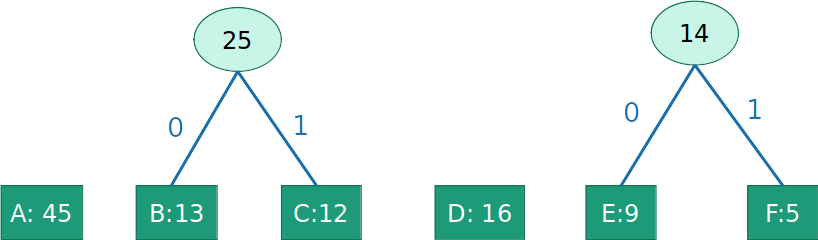
Codificação de Huffman

• Gulosamente construir sub-árvores de baixo para cima

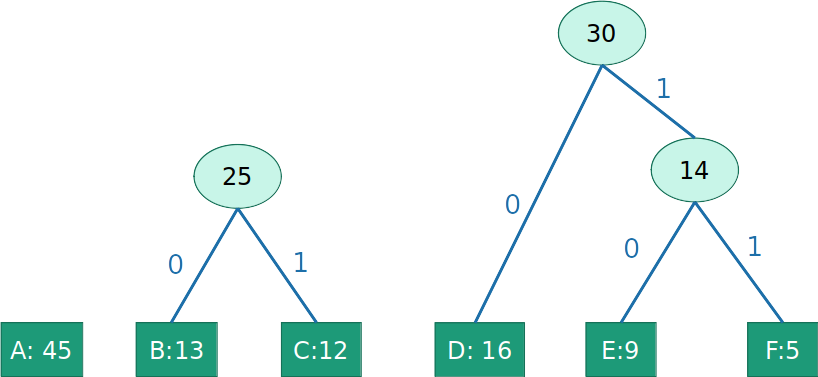
Codificação de Huffman

• Gulosamente construir sub-árvores de baixo para cima

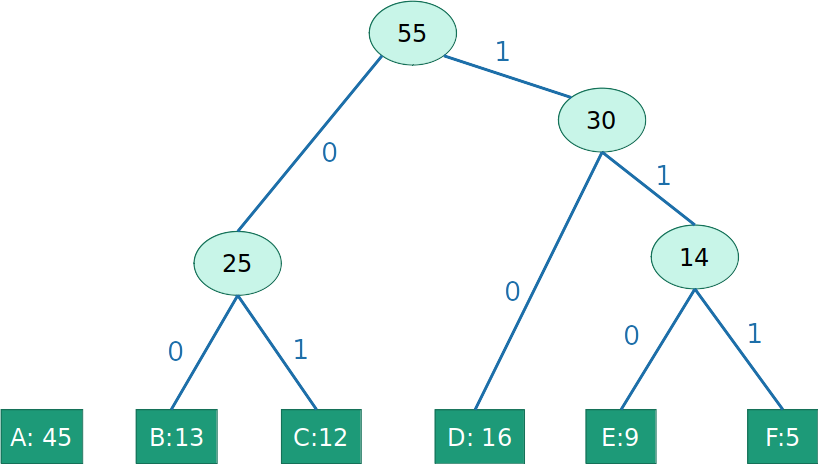
Codificação de Huffman

• Gulosamente construir sub-árvores de baixo para cima

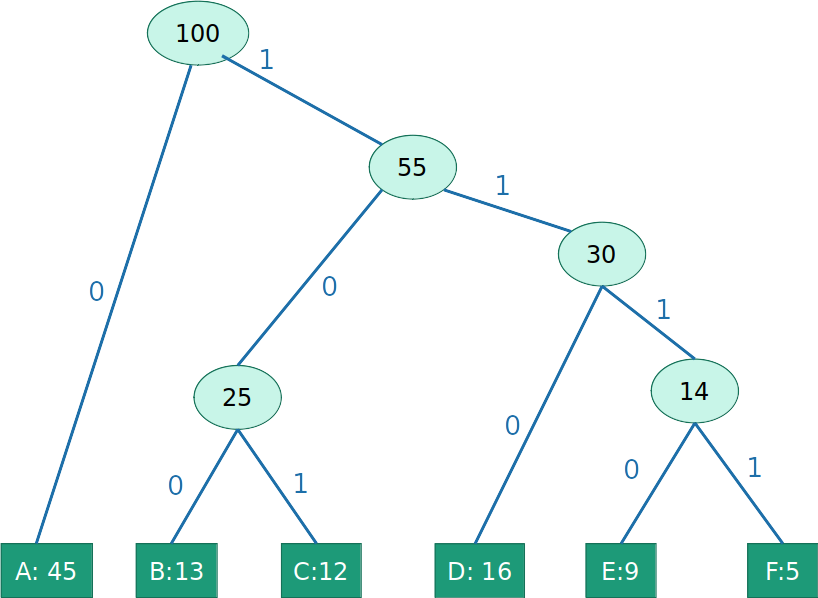
Codificação de Huffman

• Gulosamente construir sub-árvores de baixo para cima

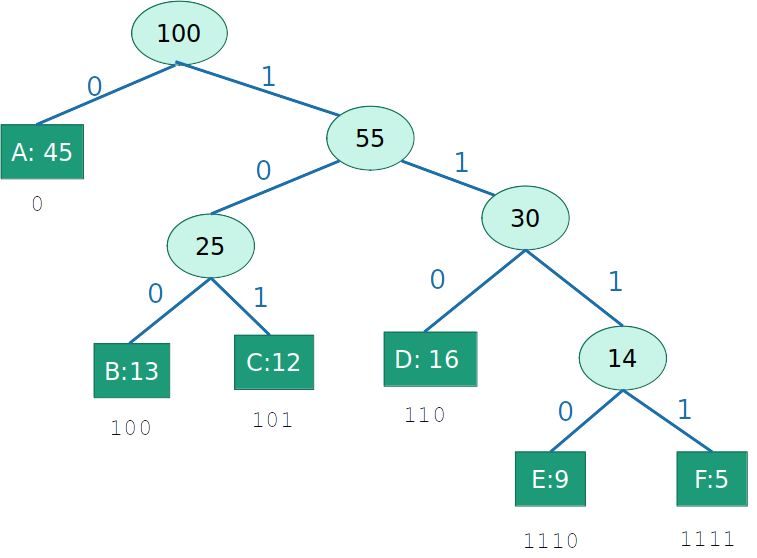
$Custo = (0,45) + 3(0,13 + 0,12 + 0,16) + 4(0,09 + 0,05) = 2,24$

Codificação de Huffman

demo

Complexidade

• Existe $\Theta(n)$ chamadas recursivas, pois essa é a quatidade de uniões que fazemos.
• Cada chamada pode levar $\Theta(n)$ para encontrar os elementos de menor frequência.
• Portanto, em uma implementação direta, o Algoritmos é $\Theta(n^2)$

Complexidade

• Entretanto, podemos usar uma heap para encontrar os elementos de menor frequência
• Dessa maneira, podemos encontrar os elementos de menor frequência em $2O(\log n) = O(\log n)$.
• A inserção da árvore unida na heap também pode ser feita em $O(\log n)$.
• Portanto, a complexidade usando heap é $O(n \log n)$

Funciona ?

• A cada passo, não excluímos uma solução ótima

Lema 1: Suponha que $x$ e $y$ são as duas letras menos frequentes. Então existe uma árvore em que $x$ e $y$ são irmãos.

Esboço de prova

• Suponha que temos uma árvore ótima $T$, e um caracter 'a' tem uma frequência $f_a \geq f_x$ de 'x', mas $d_T(a)$ 'a' tem uma distância até a raiz maior que $d_T(x)$ de 'x'

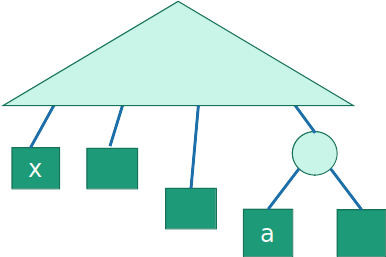
Esboço de prova

• Trocar 'a' por 'x' não pode aumentar o custo
  • 'a' é mais frequente que 'x', e fizemos a sua codificação menor com a troca

$\begin{aligned} C(T') - C(T) & = f_xd_{T}(a) + f_ad_{T}(x) - f_ad_T(a) - f_xd_T(x) \\ & = (f_x-f_a)(d_{T}(a) - d_{T}(x))\\ & \leq 0 \end{aligned}$

Esboço de prova

• Repita o processo para 'y' até que tenhamos 'x' e 'y' como irmãos

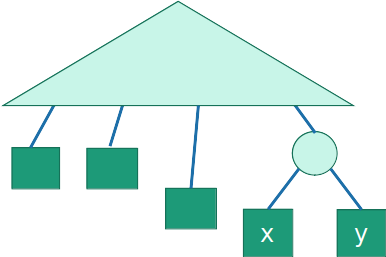
• Como 'x' e 'y' são as menos frequentes, o custo nunca aumentou. Então a árvore ainda é ótima

Esboço de prova

• O algoritmo funciona antes da primeira "junção". E após a junção, ainda funciona?

Lema 2: Uma árvore codificadora é ótima se e somente se a árvore codificadora da "combinação" de caracteres é ótima

• Em outras palavras, podemos considerar a "árvore atual" como contendo apenas folhas

Esboço de prova

- Alfabeto = {A,B,C,D,E,F}

- Alfabeto = {A,G={B,C},H={D,E,F}}

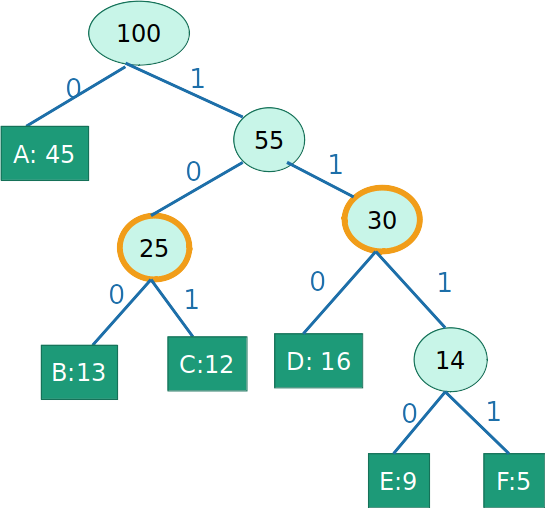
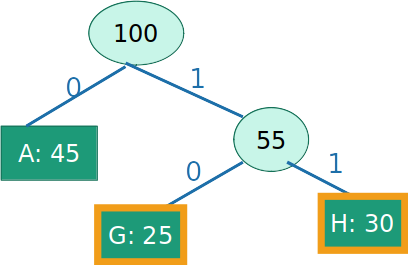
Esboço de prova

• Seja $C$ um conjunto de caracteres, e $T$ uma árvore que codifica $C$
• Seja $C'$ uma árvore em que que colapsa uma subárvore de $C$ em um único caracter $c'$, com frequência $f_{c'}$, e $T'$ uma árvore que codifica $C'$
• Seja $C'' = \{c_1^{\prime\prime}, c_2^{\prime\prime}, \cdots, c_n^{\prime\prime}\}$ os caracteres da subárvore colapsados em $c'$, então $f_{c'} = \sum_i^n c_i^{\prime\prime}$

Esboço de prova

$\begin{aligned} C(T)-C\left(T^{\prime}\right) &=\sum_{c \in C} f(c) \cdot d_{T}(c)-\sum_{c \in C^{\prime}} f(c) \cdot d_{T^{\prime}}(c) \\ &=\left(\sum_{i=1}^{r} f\left(c_{i}^{\prime \prime}\right) d_{T}\left(c_{i}^{\prime \prime}\right)\right)-f\left(c^{\prime}\right) d_{T^{\prime}}\left(c^{\prime}\right) \\ &=\left(\sum_{i=1}^{r} f\left(c_{i}^{\prime \prime}\right)\left(d_{T^{\prime \prime}}\left(c_{i}^{\prime \prime}\right)+d_{T^{\prime}}\left(c^{\prime}\right)\right)-f\left(c^{\prime}\right) d_{T^{\prime}}\left(c^{\prime}\right)\right.\\ &=\sum_{i=1}^{r} f\left(c_{i}^{\prime \prime}\right) d_{T^{\prime \prime}}\left(c_{i}^{\prime \prime}\right)+d_{T^{\prime}}\left(c^{\prime}\right) \sum_{i=1}^{r} f\left(c_{i}^{\prime \prime}\right)-f\left(c^{\prime}\right) d_{T^{\prime}}\left(c^{\prime}\right) \\ &=\sum_{i=1}^{t} f\left(c_{i}^{\prime \prime}\right) d_{T^{\prime \prime}}\left(c_{i}^{\prime \prime}\right) \end{aligned}$

• A direfença de custo só depende de $c_i^{\prime\prime}$, então $T$ é ótima se e somente se $T'$ é ótima

Em resumo:

• Lema 1 Suponha que 'x' e 'y' são os caracteres menos frequentes. Então tem uma árvore ótima em que 'x' e 'y' são irmãos.

• Lema 2 Podemos assumir que a árvore atual contém apenas folhas

• Então a cada passo não removemos nenhuma solução ótima

Passo de indução:

• Suponha que após o passo $t-1$ temos uma coleção de sub-árvores que podem ser interpretadas como "folhas" (de acordo com o Lema 2), e que fazem parte da árvore ótima

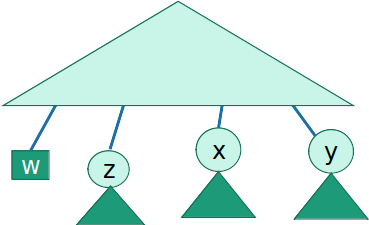
• Queremos mostrar que após o passo $t$ contendo todas as subárvores como "folhas" que fazem parte da árvore ótima

Passo de indução:

• Digamos que 'x' e 'y' são as duas menores (menos frequentes)

• De acordo com o Lema 1, existe uma sub-árvore ótima em que 'x' e 'y' são irmãos

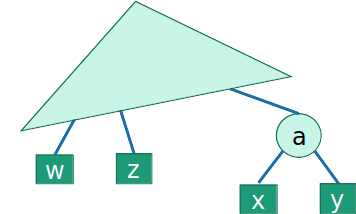
Passo de indução:

• E no passo $t$, o algoritmo une as subárvores com raíz em 'x' e 'y', criando uma nova subárvore:

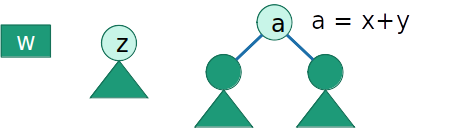
• De acordo com o Lema 2, o novo nó 'a' pode ser interpretado como uma folha, com frequência $f_a = f_x +f_y$. Portanto, após o passo $t$, continuamos com as subárvores que fazem parte da árvore ótima.

Resumindo:

• O código ASCII não é uma maneira ótima de codificar textos em línguas baseadas em alfabetos em que a distribuição das letras não é uniforme.
• A codificação de Huffman é uma maneira ótima!
• Podemos usar um algoritmo guloso para calcular a codificação de Huffman para qualquer língua.