Análise de Algoritmos
Ronaldo Cristiano Prati
Bloco A, sala 513-2
ronaldo.prati@ufabc.edu.br
Abordagem Gulosa
-
Gulosamente toma uma decisão local para reduzir o problema
-
Essa decisão faz parte da solução ótima
-
Problema tem uma sub-estrutura ótima
-
Resolução do sub-problema só depende dele mesmo
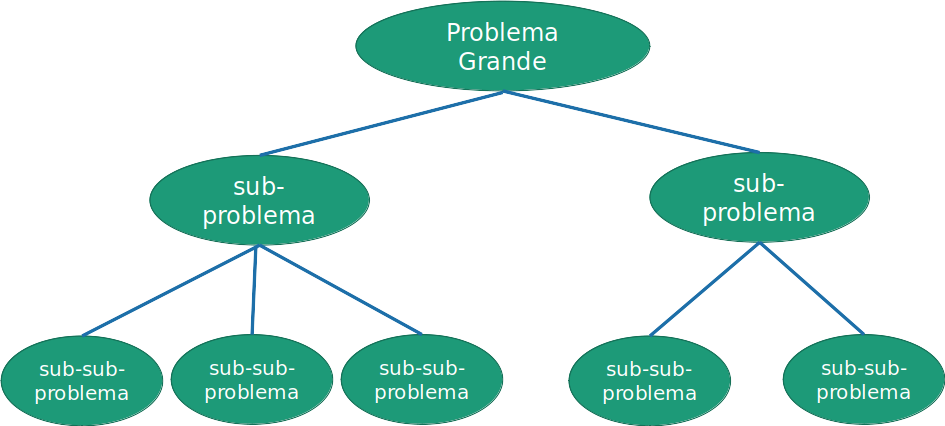
Abordagem dividir-e-conquistar
-
Divide o problema grande em problemas menores
-
(Recursivamente) resolve os problemas menores
-
Junta as soluções dos problemas menores para resolver o problema maior
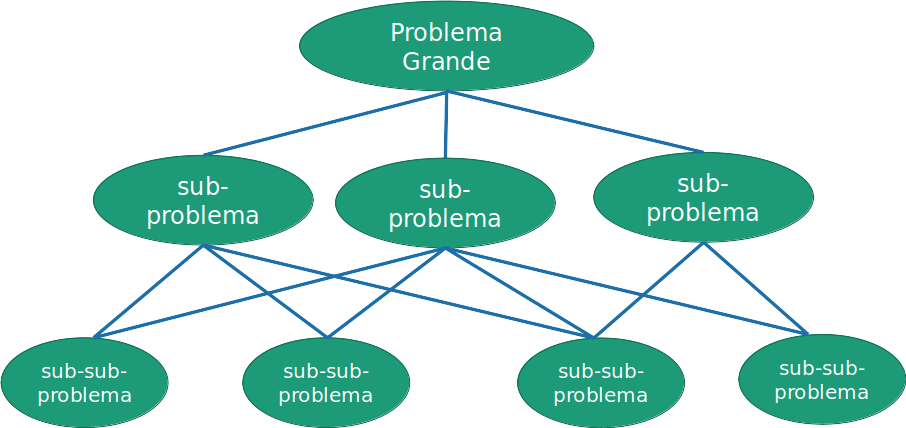
Programação dinâmica
-
Divide o problema grande em problemas menores
-
A solução do problema grande pode ser descrita em termos das soluções menores
-
Os subproblemas tem sobreposição
-
Armazena as soluções intermediárias para não precisar recalcular
Sequência de Fibonacci
- Por exemplo, considere a sequência de Fibonacci:
Fn=⎩⎪⎨⎪⎧11Fn−1+Fn−2se n=1se n=2se n>2
Sequência de Fibonacci
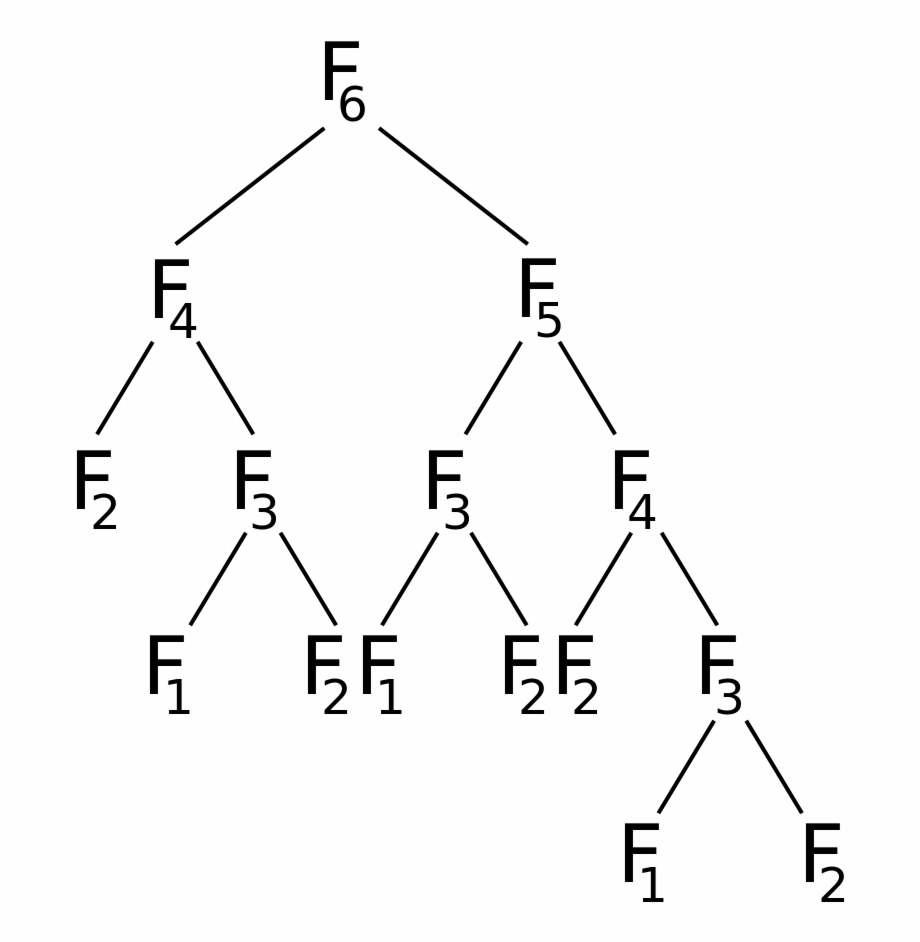
Fibonacci recursivo

- Cuja complexidade é dada pela equação de recorrência:
T(n)=T(n−1)+T(n−2)+1
Qual é a complexidade?
- Vamos usar o método da substituição para mostrar que Ω((21+5)n)
- Inicialmente, vamos mostrar que T(n)≥xn para x>1.
- Seja T(1)=1, e T(2)=3, e n≥2
- Suponha que T(m)≥xn, para 2≤m≤n−1. Assim, aplicando a T(n), temos:
T(n)=T(n−1)+T(n−2)+1≥xn−1+xn−2≥xn−2(1+x)
Qual é a complexidade?
- Note que 1+x≥x2 para (1−5)/2≤x≤(1+5)/2.
- Portanto, fazendo x=(1+5)/2 e substituindo em T(n), temos
T(n)≥(21+5)n−2(1+(21+5))≥(21+5)n−2(21+5)2=(21+5)n
Dá pra fazer melhor?
-
Observe que na abordagem puramente recursiva, precisamos resolver o mesmo problema várias vezes.
-
Podemos criar uma memória auxiliar para armzenar valores intermediários.
- Criar um vetor de tamanho n
- A medida que formos calculando Fi, armanezenamos esse valor para consultar posteriormente.
Fibonacci com memória

Fibonacci com memória
- Uma outra abordagem é preencher o vetor em uma abordagem bottom-up

Fibonacci com memória
-
Esse é um exemplo de programação dinâmica!
-
É fácil ver que a complexidade do algoritmo é O(n) já que a consulta ao vetor pode ser feita em O(1)
-
Entretanto, precisamos de uma memória auxiliar para armazenar os subproblemas já solucionados
Corte da barra de ferro
- Considere um problema em que temos uma barra de ferro de tamanho n, e queremos dividí-la em pedaços, cujos tamanho também são inteiros
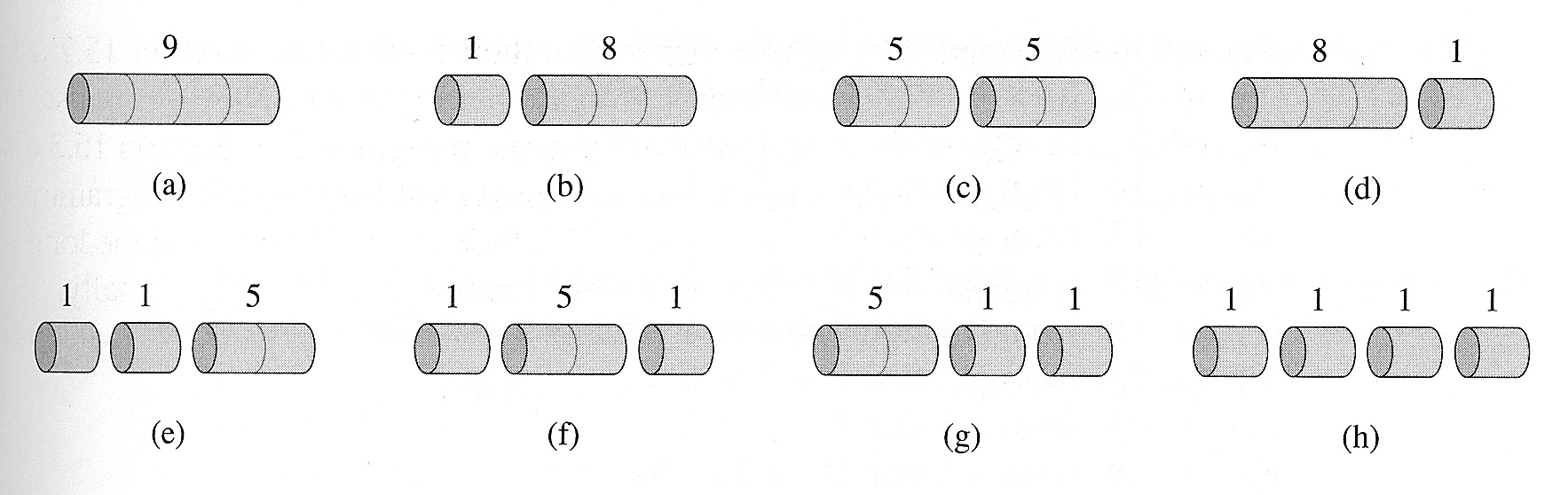
- Suponha também que os pedaços tem preços diferentes
| p1 | p2 | p3 | p4 | p5 | p6 | p7 | p8 | p9 | p10 |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 5 | 8 | 9 | 10 | 17 | 17 | 20 | 24 | 30 |
- Como cortar as barra para otimizar o lucro?
Corte da barra de ferro
| Tamanho | Lucro | Peças |
|---|---|---|
| 1 | 1 | 1 (sem corte) |
| 2 | 5 | 2 (sem corte) |
| 3 | 8 | 3 (sem corte) |
| 4 | 10 | 2 e 2 |
| 5 | 13 | 2 e 3 |
| 6 | 17 | 6 (sem corte) |
| 7 | 18 | 1 e 6 ou 2, 2 e 3 |
| 8 | 22 | 2 e 6 |
| 9 | 25 | 3 e 6 |
| 10 | 30 | 10 |
Corte da barra de ferro
- Quantas combinações de corte existem?
- Cada ponto de corte é uma variável aleatória binária (0 ou 1)
- Temos n−1 possíveis pontos de corte
- O total de possibilidades é 2n−1
Corte da barra de ferro
- Uma abordagem simplista consiste em gerar todas as possíveis combinações
- Calcular o lucro de cada uma delas
- Selecionar aquela que maximiza o lucro
- Claramente essa abordagem tem uma complexidade O(2n), já que temos 2n−1 combinações
Corte da barra de ferro
-
Uma outra possibilidade é um algoritmo recursivo
-
Um algoritmo recursivo para o problema do corte da barra escolhe uma posição pi para fazer o corte e faz uma chamada recursiva
-
Como não sabemos qual o tamanho do primeiro corte, testamos todas as possibilidades de 1 a n
Corte da barra de ferro recursivo

Corte da barra de ferro recursivo
-
A equação de recorrência desse algoritmo é
T(n)=1+i=1∑nT(n−i) -
Podemos usar o método da substituição para mostrar que esse algoritmo é O(2n). Suponha que T(m)≥2m para 0≤m≤n−1
T(n)=1+T(0)+T(1)+⋯+T(n−1)≥1+(20+21+⋯+2n−1)=2n
Corte da barra de ferro recursivo
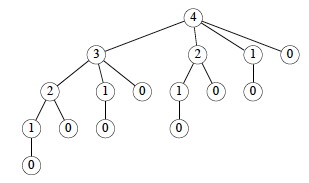
Corte da barra de ferro
-
O problema do corte da barra de ferro é um problema de otimização
-
Ele tem a propriedade de subestrutura ótima
- Você precisa saber o corte ótimo do sub-problema para calcular o corte ótimo
-
Tem uma solução recursiva exponencial
Corte da barra de ferro
- Vamos usar um vetor B de n posições para armezar o custo de um sub-problema já resolvido
- Além disso, um vetor S em que a posição S[j] indica a posição em que a barra de tamanho j deve ser cortada
Corte da barra de ferro


Abordagem BottomUP
- Também podemos ter uma abordagem BottomUp

Corte da barra de ferro
- Considerando os preços
| p1 | p2 | p3 | p4 | p5 | p6 | p7 | p8 | p9 | p10 |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 5 | 8 | 9 | 10 | 17 | 17 | 20 | 24 | 30 |
- O algoritmo calcula
| i | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| B[i] | 0 | 1 | 5 | 8 | 10 | 13 | 17 | 18 | 22 | 25 | 30 |
| S[i] | 0 | 1 | 2 | 3 | 2 | 2 | 6 | 1 | 2 | 3 | 10 |
Corte da barra de ferro
- O primeiro passo do algoritmo é verificar se o subproblema já foi resolvido.
- Caso não esteja resolvido, ele faz isso de uma maneira parecida com o algoritmo
CorteBarra. - A diferença é que o primeiro local pra fazer o corte de uma barra de tamanho i é armazenada em S[i], e o maior lucro em B[i].
Complexidade
- Observe que a cada chamada de
CorteBarraRecursivoTopDown, um subproblema que já foi resolvido retorna imediatamente. - As demais linhas são executadas em tempo constante.
- Como armazenamos o resultado sempre que resolvemos um subproblema, cada subproblema é resolvido uma vez.
- O tempo de execução é então
T(m)=1+2+⋯+m=Θ(m2)
Impressão dos Cortes
- Para saber os pontos de corte, podemos percorrer o vertor S[i] para encontrar os pontos de corte.
- Observe que em S[n], temos o tamanho do primeiro corte.
- Após esse corte, a barra tem tamanho n−S[−]

Mochila inteira
- Dado um conjunto I={1,2,⋯,n} contendo n itens
- Cada item i∈I tem um peso wi e um valor vi
- Como podemos selecionar um subconjutno de S⊆I uma mochila com capacidade W tal que:
- O peso dos itens selecionados cabe na mochila: ∑i∈Swi≤W
- O valor dos itens selecionados é maximo: max∑i∈Svi
Mochila inteira
- Por exemplo, dado o seguinte conjunto de itens
| item | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| peso | 6 | 2 | 4 | 3 | 11 |
| valor | 20 | 8 | 14 | 13 | 35 |
- Como podemos selecionar itens para preencher uma mochila de tamanho 10?
Mochila inteira
- Podemos resolver o problema por força bruta enumerando todos os subconjuntos possíveis
- Verificar quais subconjuntos cabem na mochila
- Calcular o valor total dos suconjuntos que cabem e armazenar o maior deles
Quantos subconjuntos existem?
- Para cada item, temos a opção de colocá-lo ou não
- Temos um total de 2n subconjuntos
- Para cada conjunto, levamos O(n) para verificar se os itens cabem na mochila e qual é o seu valor total
- Ou seja, esse algoritmo leva temp O(n2n)
Subestrutura do problema
- Seja uma instância do problema por K(In,v,wW), em que:
- In={1,2,⋯,n} um conjunto de itens
- v é uma lista dos valores dos itens
- w é uma lista dos pesos dos itens
- W é a capacidade da mochila
Subestrutura do problema
-
S∗ é uma solução ótima para K(In,v,w,W), e S∗⊆,In com um valor total ótimo Vn,W=∑i∈S∗vi
- Se n∈/S, então S∗ também é uma solução para K(In−1,W)
- Se n∈S, então S∗ também é uma solução para K(In−1,W−wn)
-
Como saber se n está em S∗?
- Máximo entre selecionar ou não o item n, se ele cabe na mochila
- Valor do problema desconsiderando o item n, se ele não cabe na mochila
Vn,W={max{Vn−1,W,Vn−1,W−wn+vn}Vn−1,W se wn≤W se wn>W
Mochila inteira
Mochila inteira
- Uma solução direta recursiva baseada nessa regra:

Mochila inteira
-
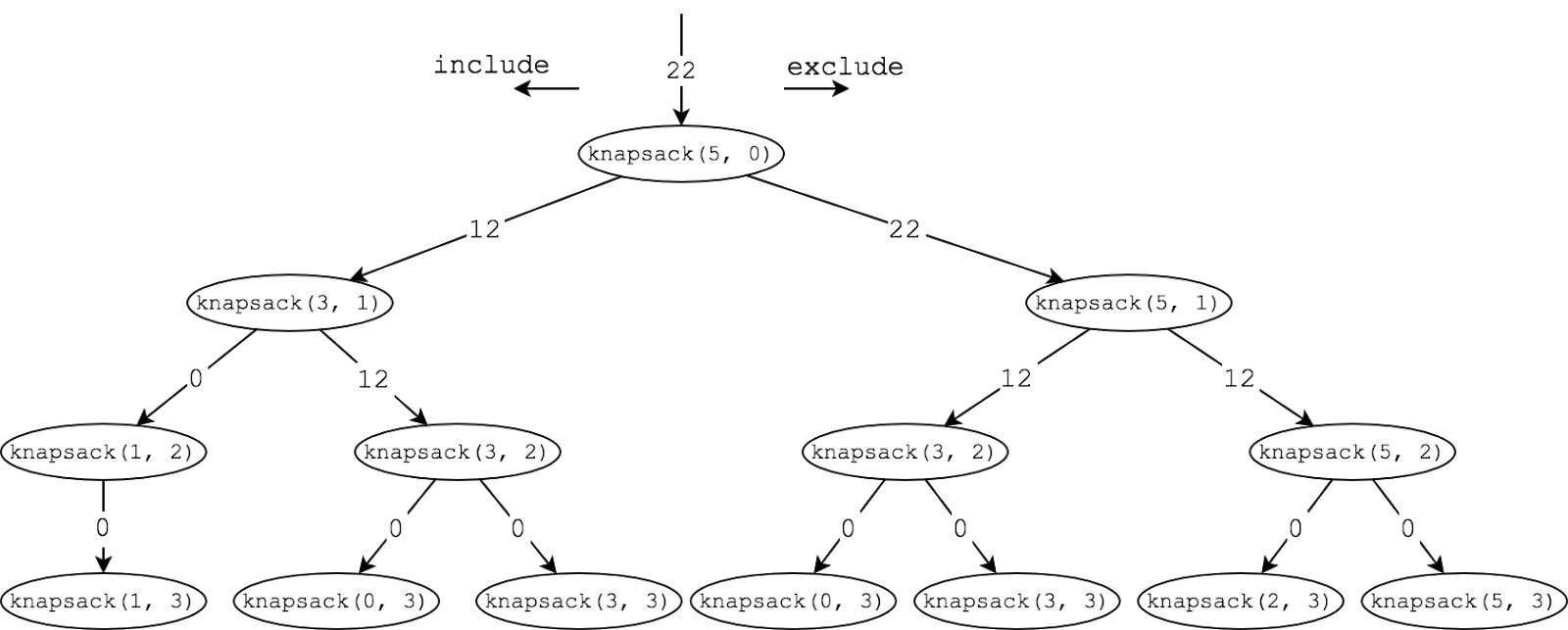
A equação de recorrência para esse algoritmo é T(n)=2(Tn−1), cuja solução é O(2n)
-
Olhando a árvore de recursão, é fácil perceber que esse algoritmo resolve o mesmo subproblema várias vezes.
-
Observe que os subproblemas dependem tanto do número de itens n, quanto da capacidade W do subproblema.
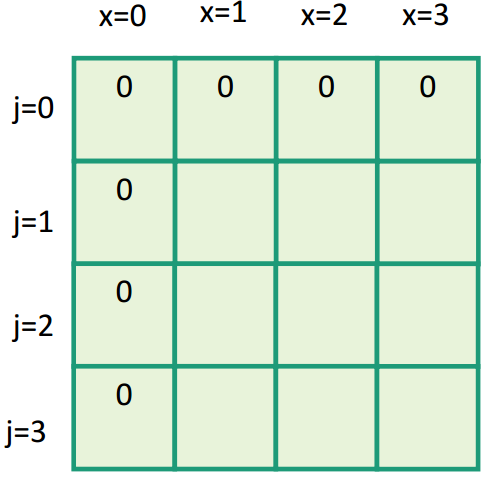
- Poderíamos armazenar as soluções usando um vetor de tamanho nW
- Entretanto, usar uma matriz n×W facilita a indexação
Mochila inteira

Mochila inteira

Mochila inteira
| item | 1 | 2 | 3 |
|---|---|---|---|
| peso | 1 | 2 | 3 |
| valor | 1 | 4 | 6 |
Mochila inteira
| item | 1 | 2 | 3 |
|---|---|---|---|
| peso | 1 | 2 | 3 |
| valor | 1 | 4 | 6 |
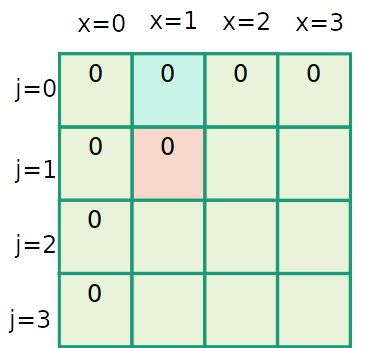
Mochila inteira
| item | 1 | 2 | 3 |
|---|---|---|---|
| peso | 1 | 2 | 3 |
| valor | 1 | 4 | 6 |
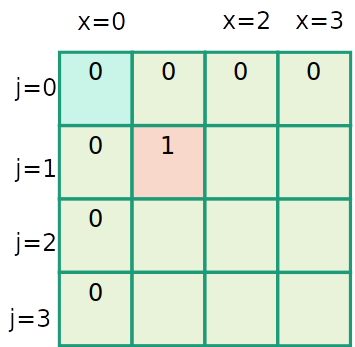
Mochila inteira
| item | 1 | 2 | 3 |
|---|---|---|---|
| peso | 1 | 2 | 3 |
| valor | 1 | 4 | 6 |
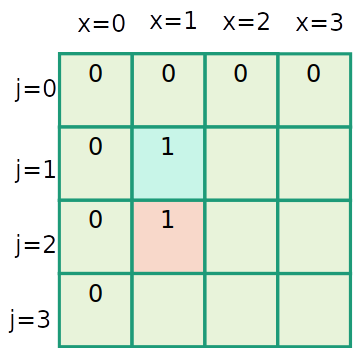
Mochila inteira
| item | 1 | 2 | 3 |
|---|---|---|---|
| peso | 1 | 2 | 3 |
| valor | 1 | 4 | 6 |
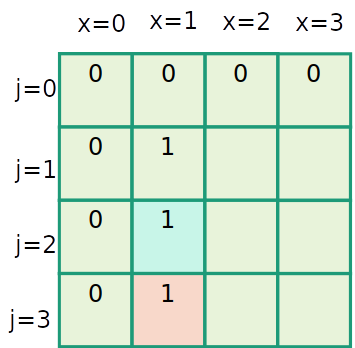
Mochila inteira
| item | 1 | 2 | 3 |
|---|---|---|---|
| peso | 1 | 2 | 3 |
| valor | 1 | 4 | 6 |
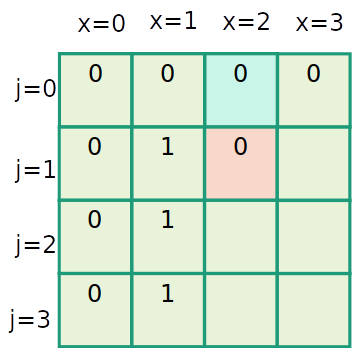
Mochila inteira
| item | 1 | 2 | 3 |
|---|---|---|---|
| peso | 1 | 2 | 3 |
| valor | 1 | 4 | 6 |
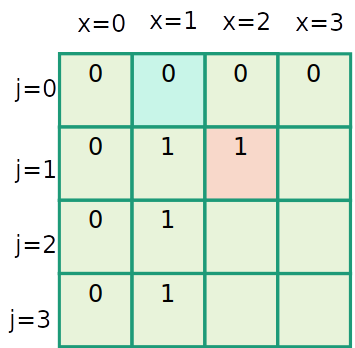
Mochila inteira
| item | 1 | 2 | 3 |
|---|---|---|---|
| peso | 1 | 2 | 3 |
| valor | 1 | 4 | 6 |
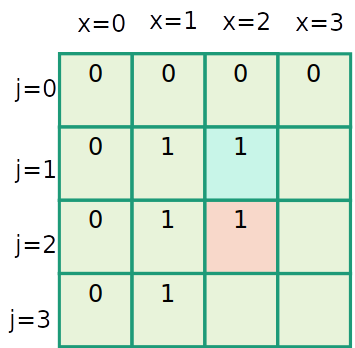
Mochila inteira
| item | 1 | 2 | 3 |
|---|---|---|---|
| peso | 1 | 2 | 3 |
| valor | 1 | 4 | 6 |
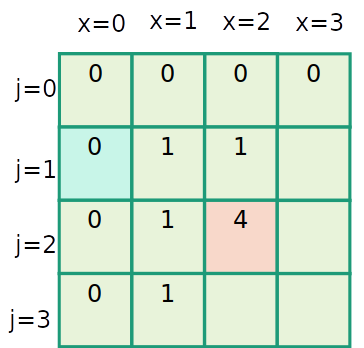
Mochila inteira
| item | 1 | 2 | 3 |
|---|---|---|---|
| peso | 1 | 2 | 3 |
| valor | 1 | 4 | 6 |
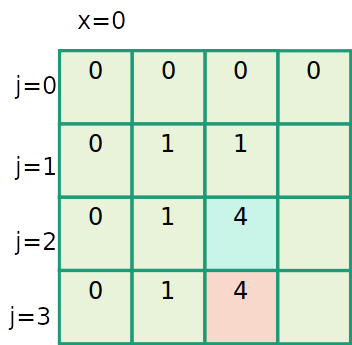
Mochila inteira
| item | 1 | 2 | 3 |
|---|---|---|---|
| peso | 1 | 2 | 3 |
| valor | 1 | 4 | 6 |
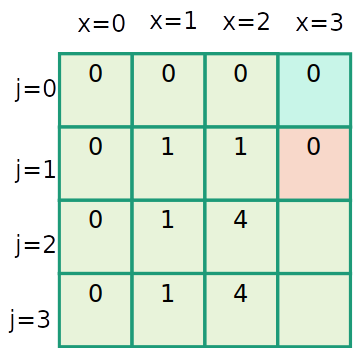
Mochila inteira
| item | 1 | 2 | 3 |
|---|---|---|---|
| peso | 1 | 2 | 3 |
| valor | 1 | 4 | 6 |
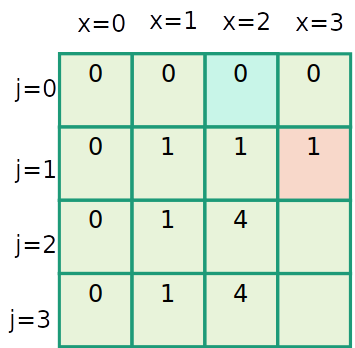
Mochila inteira
| item | 1 | 2 | 3 |
|---|---|---|---|
| peso | 1 | 2 | 3 |
| valor | 1 | 4 | 6 |
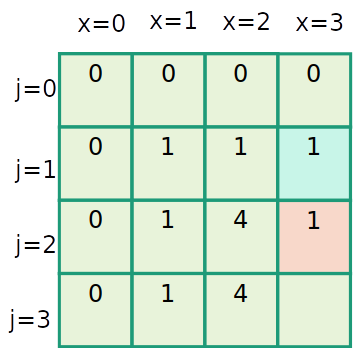
Mochila inteira
| item | 1 | 2 | 3 |
|---|---|---|---|
| peso | 1 | 2 | 3 |
| valor | 1 | 4 | 6 |

Mochila inteira
| item | 1 | 2 | 3 |
|---|---|---|---|
| peso | 1 | 2 | 3 |
| valor | 1 | 4 | 6 |
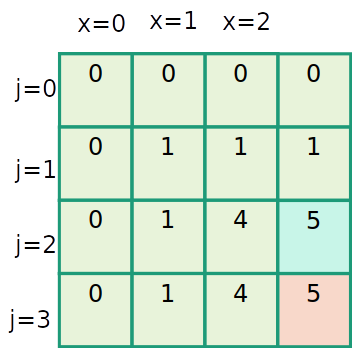
Mochila inteira
| item | 1 | 2 | 3 |
|---|---|---|---|
| peso | 1 | 2 | 3 |
| valor | 1 | 4 | 6 |
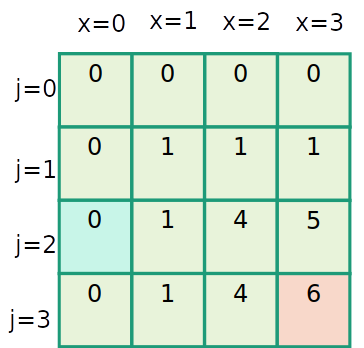
Mochila inteira
| item | 1 | 2 | 3 |
|---|---|---|---|
| peso | 1 | 2 | 3 |
| valor | 1 | 4 | 6 |
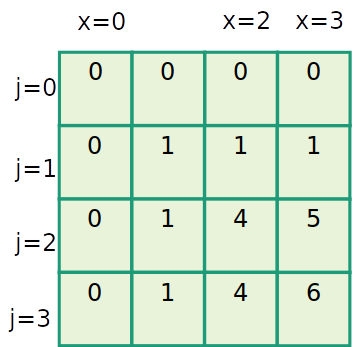
Imprimindo a mochila
-
Na última célula da matriz M[n][W] contém o valor ótimo.
-
Mas não sabemos quais itens devem estar na mochila
-
No entanto, a maneira como a matriz foi preenchida nos permite obter quais são esses elementos
Imprimindo a mochila

Complexidade
-
É fácil perceber que a complexidade do algoritmo é proporcioal ao tamanho da matriz, ou seja O(nW)
-
No entanto, observe que precisamos de uma coluna na tabela para cada possível tamanho da mochila dos subproblemas. Esse número, no entanto, não é polinomial no tamanho do da entrada
-
Considerando pesos inteiros, teríamos O(2logW) possíveis valores para W, e a complexidade do algoritmo é O(n2logW)
-
Esse algoritmo é o que chamamos de pseudo-polinomal
Programação dinâmica
- Identificar subestrutura ótima
- Encontrar uma formulação recursiva
- Usar programação dinâmica para encontrar o valor da função ótima
- Se necessário, armazenar informação adicional de tal maneira que no passo 3 podemos encontrar a solução ótima