Análise de Algoritmos
Ronaldo Cristiano Prati
Bloco A, sala 513-2
ronaldo.prati@ufabc.edu.br
Programação dinâmica
- Armazena uma tabela com solução de (sub)problemas já resolvidos
- Essa estratégia é chamada de memorização
- Usa as soluções da tabela para resolver problemas ainda não resolvidos
- Ao final, usamos a informação coletada no caminho para resolver o problema completo
Programação dinâmica
- Duas abordagens
-
Top Down: geralmente a transcrição direta de um algoritmo recursivo
-
Bottom up: inicia pelos problemas menores e usa essa solução para resolver problemas maiores
-
Programação dinâmica
- O nome "dinâmica" se refere ao fato que o problema é resolvido em multiplos estágios
- O nome foi atribuído (junto com a criação da técnica) nos anos de 1950
- Precisava de um "nome bonito" para conseguir financiamento da força aérea americana:
“It’s impossible to use the word, dynamic, in the pejorative sense...I thought dynamic programming was a good name. It was something not even a Congressman could object to.”
Subsequência Comum
-
A sequência BDFH é uma subsquência de ABCDEFGH
- Observe que não precisam, necessariamente, serem contínuos
-
Se X e Y são sequências, uma subsequência comum é uma subsequência de ambas as sequências.
- BDFH é uma subsequência de ABCDEFGH e ABDFGHI
Subsequência Comum Máxima
-
A maior subsequência comum é uma sequência que é comum e é a mais longa.
- A maoir subsequência comum entre ABCDEFGH and ABDFGHI é ABDFGH.
-
Problema: Dados duas sequências X={X1,X2,⋯,Xm} e Y={Y1,Y2,⋯,Yn}, encontrar uma subsquência de maior tamanho LCS(X,Y)
Aplicações
- Bioinformática:
- Encontrar a semelhança genética entre espécies; Encontrar sequências comuns para uma detarminada característica/doença genética
- Diferença entre arquivos:
- Comando
diffdo do unix
- Comando
- Merge em controlo de versões
svn,git, etc.
- Processamento de Língua Natural
- pareamento de sentenças
Maior Subsequência comum
-
Solução por força bruta:
- Enumerar todas as possíveis subsequências de X. Checar se cada uma dessas subsquências também é subsequência de Y, guardando a de maior comprimento.
-
Complexidade?
- Existem 2m subsequências de X
- Tempo linear para verificar se a subsequência de X está em Y
- O(n2m), portanto ineficiente
Programação dinâmica
- Identificar subestrutura ótima
- Encontrar uma formulação recursiva
- Usar programação dinâmica para encontrar o valor da função ótima
- Se necessário, armazenar informação adicional de tal maneira que no passo 3 podemos encontrar a solução ótima
Subestrutura ótima
- Vamos definir um prefixo como uma subsequência que se inicia na primeira, até uma certa posição i
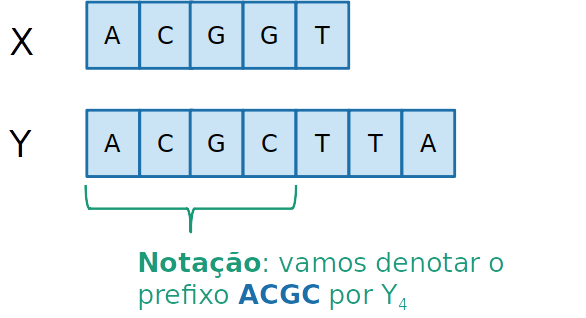
Subestrutura ótima
- Seja C[i,j] o tamanho da maior subsquência comum entre Xi e Yj
C[4,4]=3
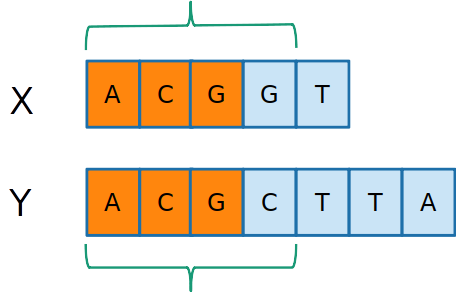
Subestrutura ótima
- Seja C[i,j] o tamanho da maior subsquência comum entre Xi e Yj
C[2,3]=4
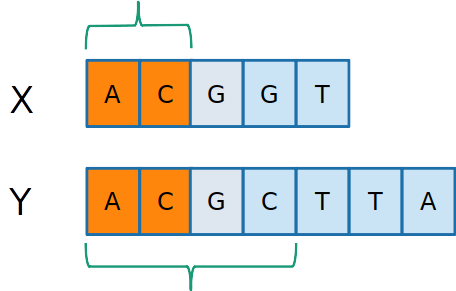
Formulação recursiva
-
Seja X e Y duas sequências de tamanho i e j, nas quais queremos encontrar a maior sequência comum.
-
Vamos tentar escrever C[i,j] em função de problemas menores
- Seja X[i] e Y[j] os dois últimos caracteres da sequência:
Ci,j=⎩⎪⎨⎪⎧01+Ci−1,j−1max(Ci−1,j,Ci,j−1)se i=0 ou j=0se X[i]=Y[j]se X[i]=Y[j]
Formulação recursiva
- Se X[i]=Y[j], então
Ci,j=1+Ci−1,j−1
uma vez que as duas últimas posições são iguais (portanto a subsequência máxima entre os dois últimos caracteres é 1),
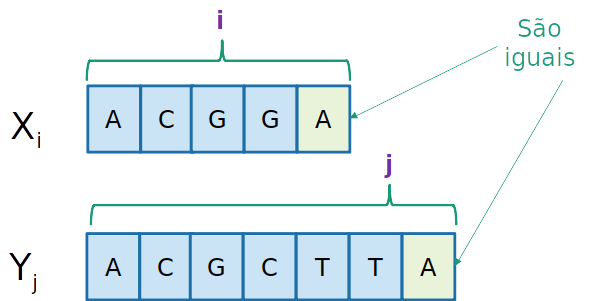
Formulação recursiva
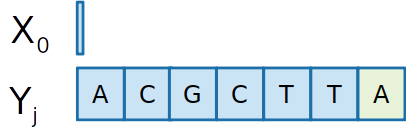
- Se i=0 ou j=0, então C[i,j]=0 uma vez que
- Ou X ou Y não contém nenhum caracter, e não tem nenhuma subsequência em comum.
Formulação recursiva
- Se X[i]=Y[j], então Ci,j=1+Ci−1,j−1
uma vez que- as duas últimas posições são iguais (portanto a subsequência máxima entre os dois últimos caracteres é 1),
- e devemos continuar verificando o restante da subsquência

Formulação recursiva
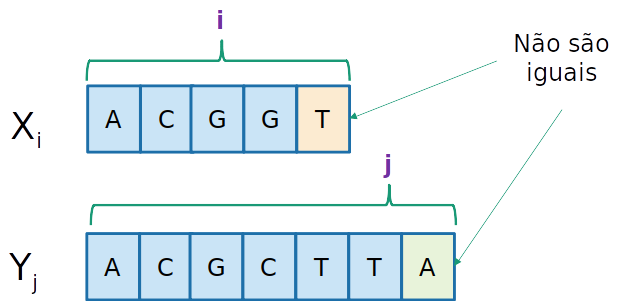
- Se X[i]=Y[j], então max(Ci−1,j,Ci,j−1) uma vez que
- A subsequência máxima pode se dar ignorando o último caracter da primera sequência
- A subsequência máxima pode se dar ignorando o último caracter da segunda sequência
Formulação recursiva
-
Uma LCS(X,Y) pode ser obtida recursivamente da seguinte maneira:
- Se Xm=Yn, eles fazem parta de LCS, e deve-se continuar procurando em LCS(Xm−1,Yn−1)
- Se Xm=Yn, então temos dois subproblemas
- Encontrar uma LCS(Xm−1,Yn);
- Encontrar uma LCS(Xm,Yn−1);
- LCS(X,Y) é a maior entre essas duas.
-
A complexidade desse algoritmo é O(2(m+n))
Formulação recursiva
- Observe também que há um overlap entre os subproblemas
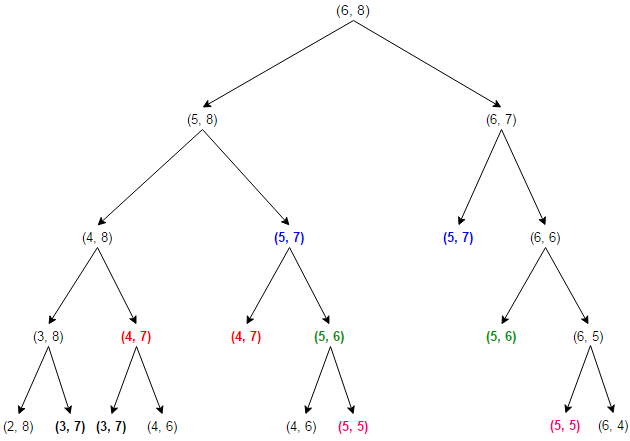
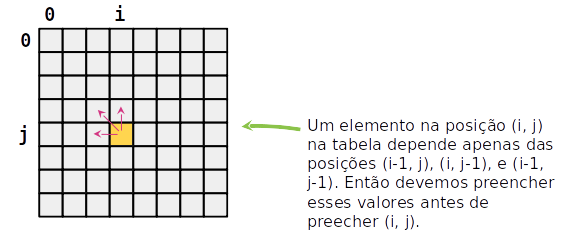
Programação Dinâmica
- Assim com no problema da mochila inteira, vamos usar uma matriz para armazenar os valores de Ci,j já calculados
Ci,j=⎩⎪⎨⎪⎧01+Ci−1,j−1max(Ci−1,j,Ci,j−1)se i=0 ou j=0se X[i]=Y[j]se X[i]=Y[j]
Programação Dinâmica
- A matriz é criada com uma linha e coluna a mais, inicialmente preenchida com zeros
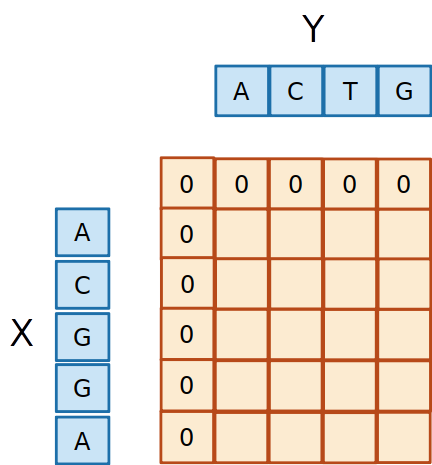
Programação Dinâmica
- Preenchemos a matriz de acordo com os três casos possíveis até completar a matiz
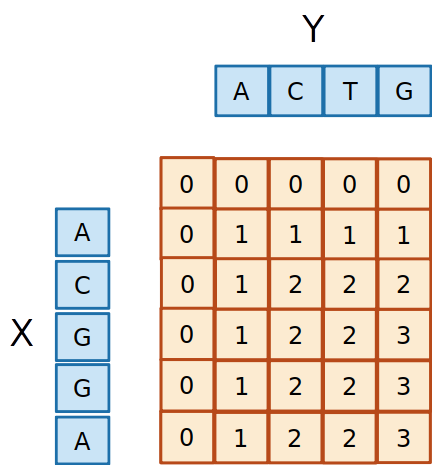
Programação Dinâmica
- O tamanho da maior subsequência comum está na última posição da matriz
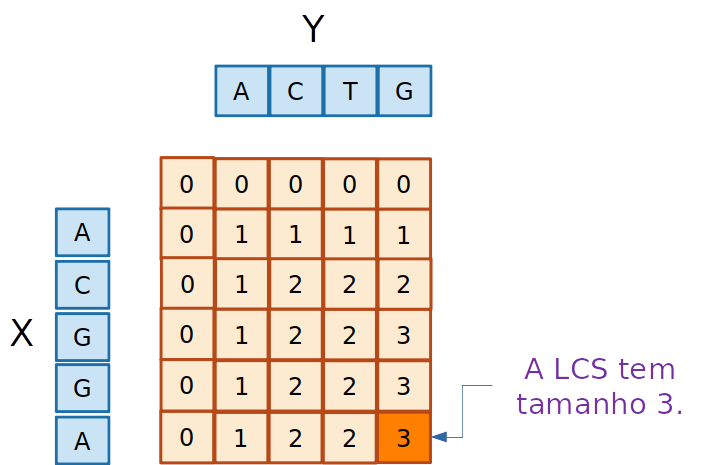
Programação Dinâmica
- Os dois caracteres são diferentes, então o
3deve ter vindo do3de cima
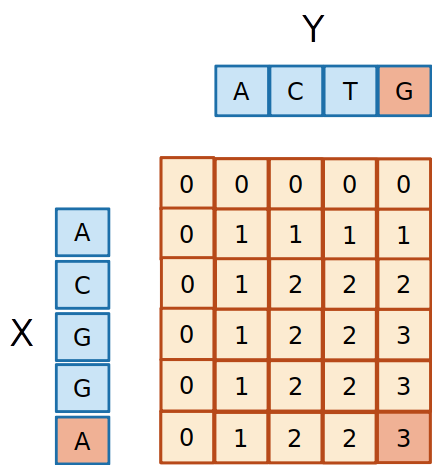
Programação Dinâmica
- Os dois caracteres são iguais, então o
3deve ter vindo desta célula
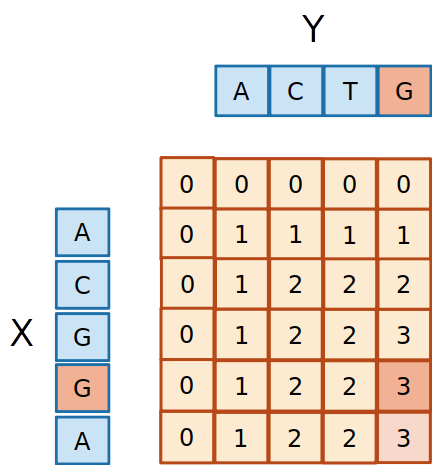
Programação Dinâmica
- Como a última iteração foi um match, devemos nos mover na diagonal
- Como os dois elementos são diferentest, o
2pode ter vindo tanto da esquerda quanto de cima
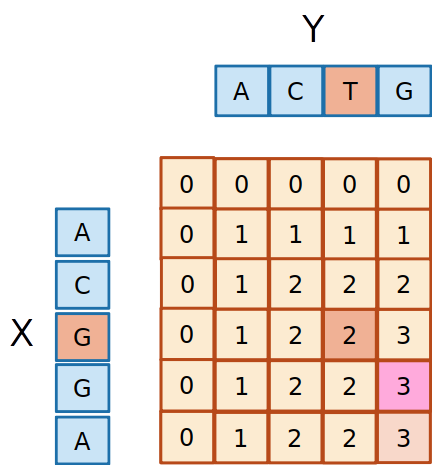
Programação Dinâmica
- Digamos que escolhemos a de cima
- Como os dois caracteres são diferentes, e o valor da célula de cima é menor que o da esquerda, o
2deve ter vindo da esquerda
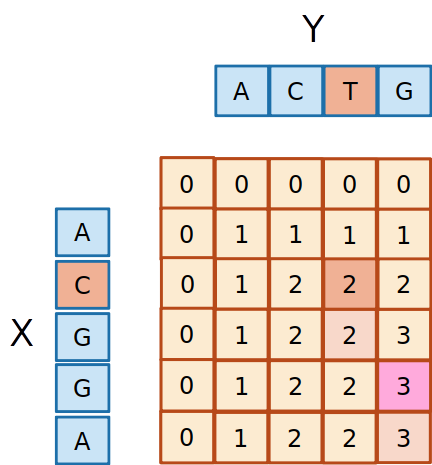
Programação Dinâmica
- Os dois caracteres são iguais, então o
2deve ter vindo desta célula
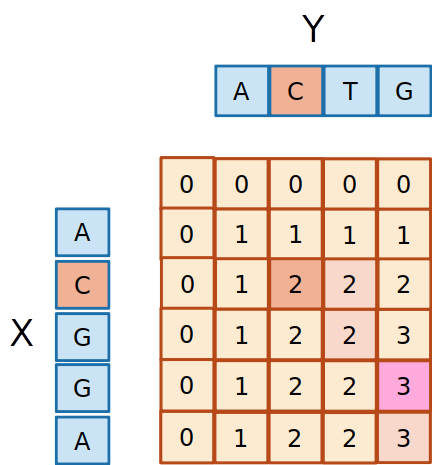
Programação Dinâmica
- Os dois caracteres são iguais, então o
1deve ter vindo desta célula
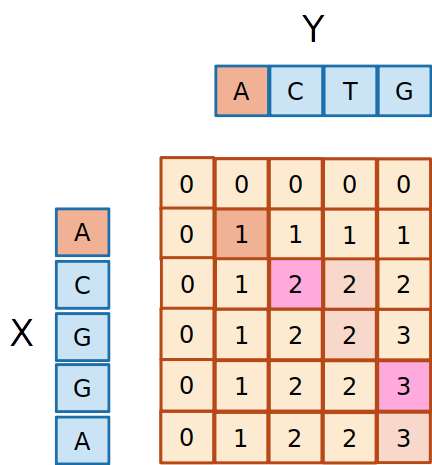
Programação Dinâmica
- Chegamos ao final das duas subsequências, a maior subsequência comum correspondem aquelas em houve um match. Nesse caso, ACG
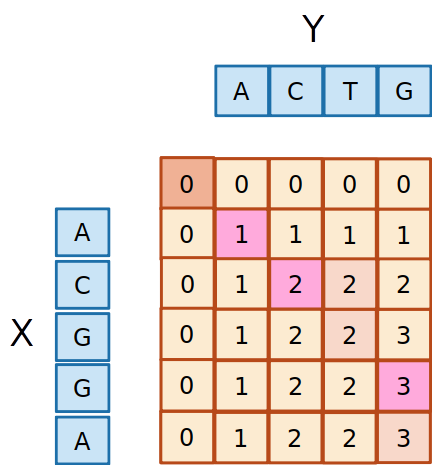
Algoritmo

Algoritmo

Complexidade
- É fácil ver que a complexidade do algoritmo é O(mn), com um custo adicional de memória de O(mn)
Algoritmo Needleman-Wunsch
- Quando dois caracteres são iguais, temos um
match - Quando há um buraco, temos um
gap - Em algumas situações, queremos dar pesos diferentes ao
matche aogap- Esse é um requisito comum em análise de DNA, em que queremos evitar buracos muito grandes no aninhamento
- Eventualmente, podemos também permitir
matchpor similaridade- Por exemplo,
seztem um som parecido
- Por exemplo,
Algoritmo Needleman-Wunsch
-
Seja α(a,b) uma função que retorna o benefício/penalidade de alinhar os caracteres a e b (que podem ou não serem iguais)
-
Seja α(gap) a penalidade de alinhar um caracter com um gap
-
O Algoritmo de Needleman-Wunsch é similar ao algoritmo de encontrar uma subsequência máxiama, mas com o objetivo é encontrar o alinhamento de pontuação máxima
Algoritmo Needleman-Wunsch
- Para o algoritmo de Needleman-Wunsch, definimos uma matriz de pontuação em que os pesos são definidos por
Pi,j=max⎩⎨⎧α(xi,yj)+Pi−1,j−1α(gap)+Pi−1,jα(gap)+Pi,j−1
Algoritmo Needleman-Wunsch

Algoritmo Needleman-Wunsch
- É fácil ver que a complexidade é a mesma do algoritmo que encontra a maior subsquência máxima