Análise de Algoritmos
Ronaldo Cristiano Prati
Bloco A, sala 513-2
ronaldo.prati@ufabc.edu.br
Caminho mais Curto
-
Já vimos que a busca em largura é capaz de encontrar a menor distância de um certo nó para qualquer outro nó para grafos não ponderados
- Como cara arestas não tem pesos (ou equivalentemente tem o mesmo peso), a distância entre vértices é dada pelo número de areastas
-
E se areastes tiverem peso?
- O tamanho de um caminho é dado pela soma dos pesos das arestas daquele caminho
Caminho mais Curto de única fonte
-
Problema Dados um grafo G=(V,E), uma função w de peso nas arestas e um vértice s∈V(G), calcular a distância mínima distGw(s,v) para todo v∈V(G).
-
Em outras palavras, queremos encontrar a distância mínima a partir de uma fonte s qualquer do grafo para todos os outros nós do grafo
- Se o nó v não é alcançável a partir de s, distGw(s,v)=∞
Caminho mais Curto
Afirmação: Um subcaminho de um caminho mais curto também é um caminho mais curto
- Intuição:
- Suponha que esse seja o caminho mais curto de s a t

- Suponha que esse seja o caminho mais curto de s a t
Caminho mais Curto
Afirmação: Um subcaminho de um caminho mais curto também é um caminho mais curto
- Intuição:
- Suponha que esse seja o caminho mais curto de s a t
- E que nesse caminho exista um subcaminho de s e passando por x

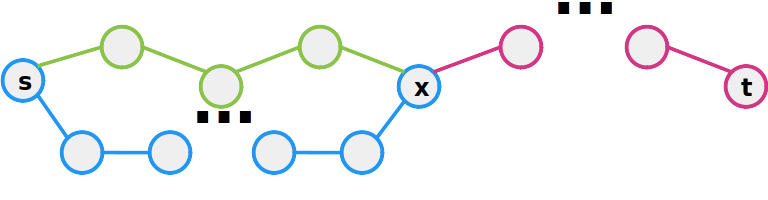
Caminho mais Curto
Afirmação: Um subcaminho de um caminho mais curto também é um caminho mais curto
- Intuição:
- Suponha que esse seja o caminho mais curto de s a t
- E que nesse caminho exista um subcaminho de s e passando por x
- Se existir um outro caminho de s a x ele tem que ser maior ou igual que o subcaminho do caminho ótimo
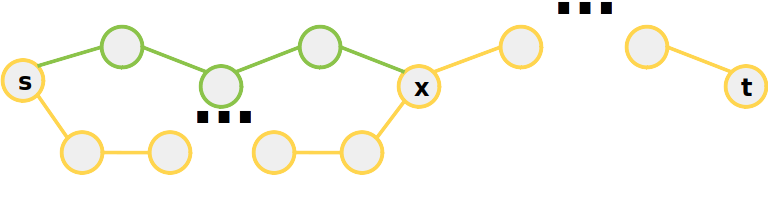
Caminho mais Curto
Afirmação: Um subcaminho de um caminho mais curto também é um caminho mais curto
- Intuição:
- Suponha que esse seja o caminho mais curto de s a t
- E que nesse caminho exista um subcaminho de s e passando por x
- Se existir um outro caminho de s a x ele tem que ser maior ou igual que o subcaminho do caminho ótimo (senão ele seria o ótimo)
Algorithmo de Dijkstra
-
O algoritmo de Dijkstra resolve o problema, e os pesos das areastas forem todos positivos
-
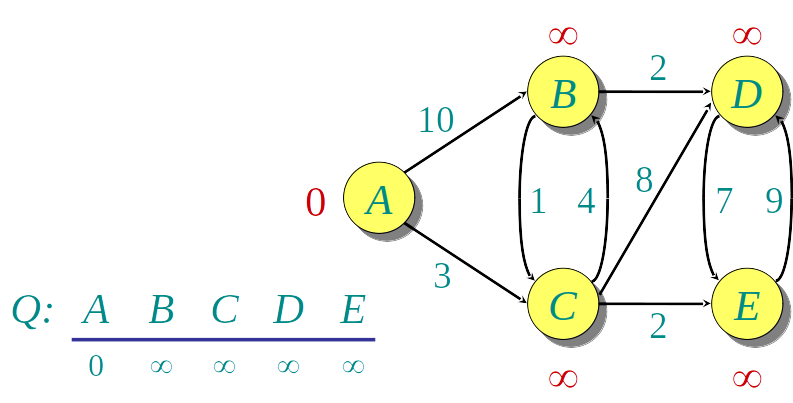
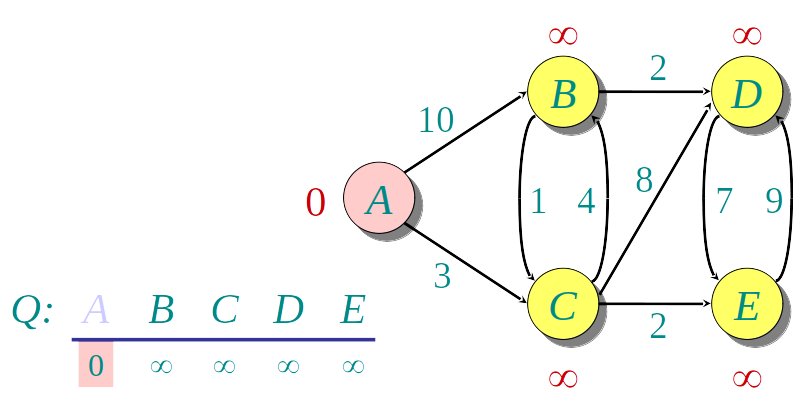
A distância v.distance para os nós v∈G é inicializada com ∞ e para a fonte é inicializada 0
-
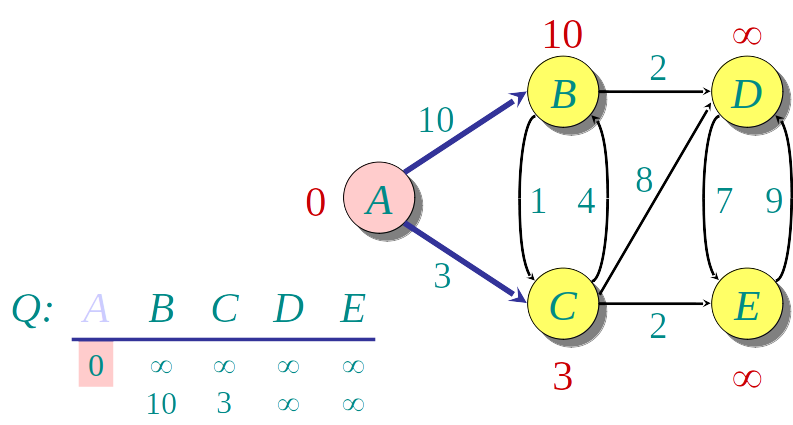
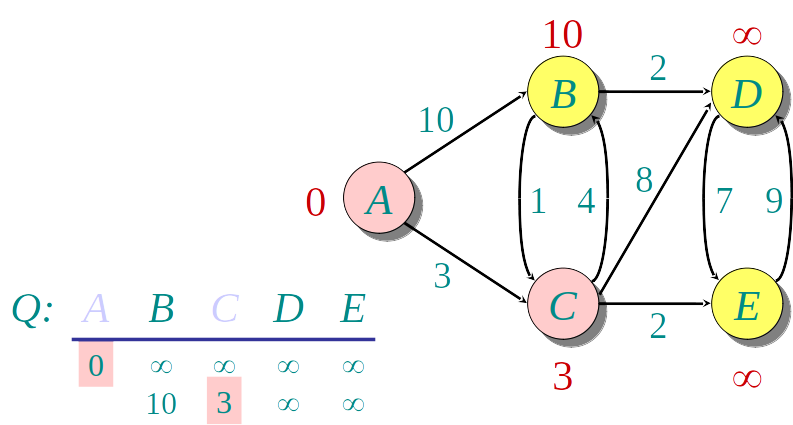
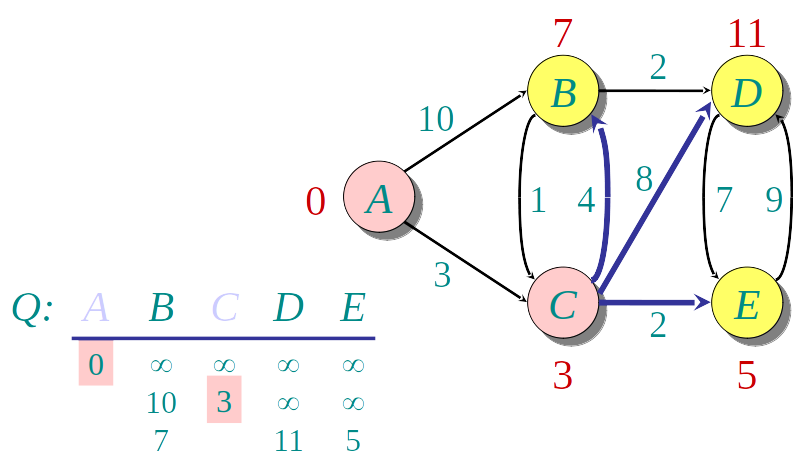
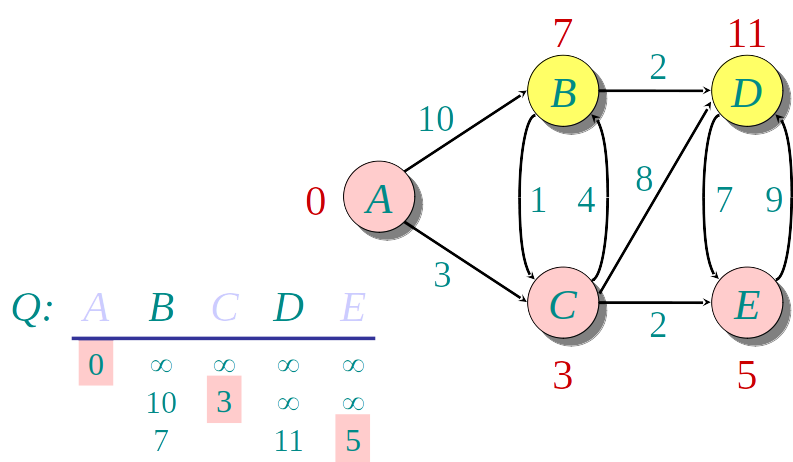
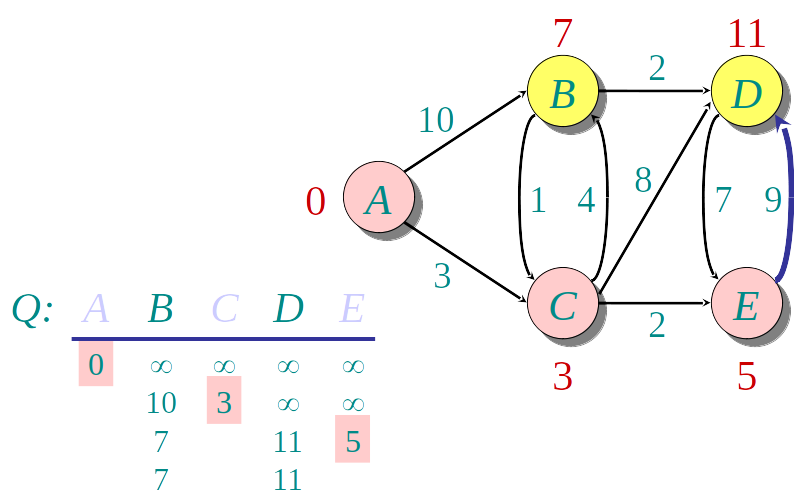
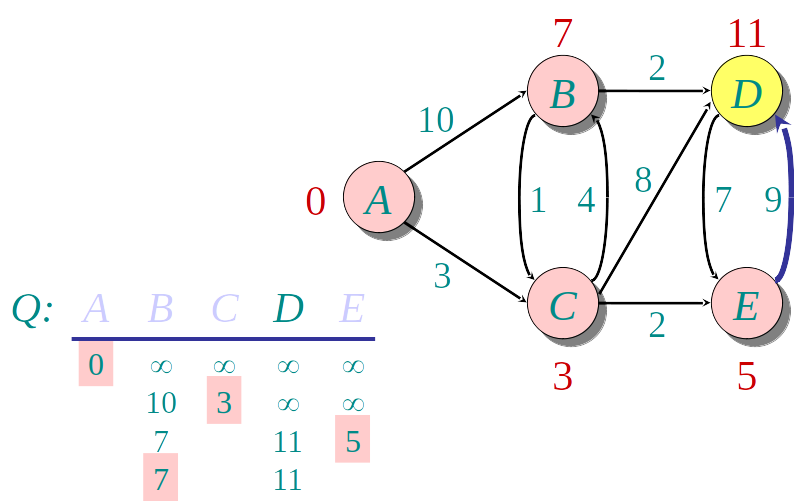
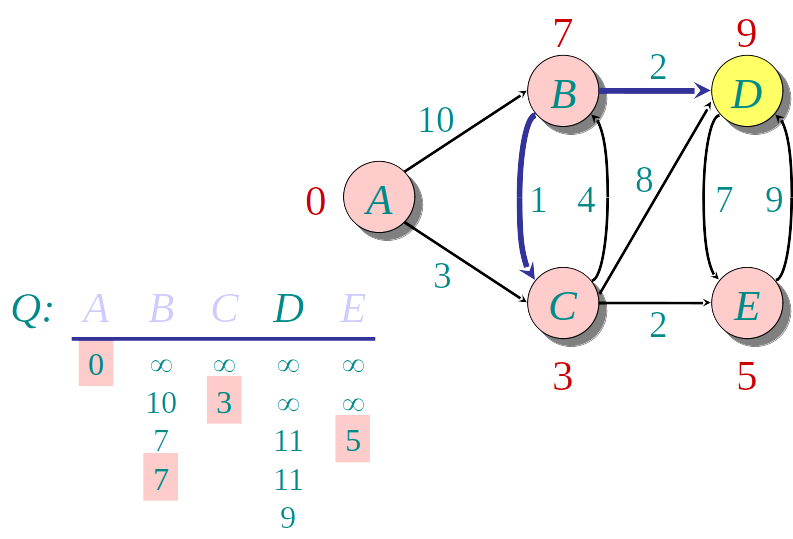
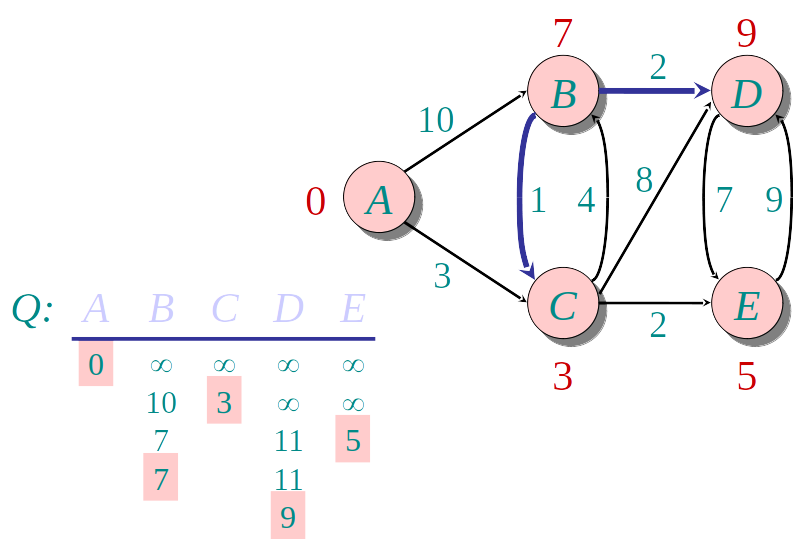
Algoritmo guloso: a cada etapa descobre a menor distância para um novo vértice u, e "relaxa" a distância para os demais
- Seleciona o vértice u de menor distância
- Relaxa a distância dos vizinhos v de u usando a fórmula:
v.distancia=min(v.distancia,u.dista^ncia+w(uv))
Algorithmo de Dijkstra
-
Usamos um apontador para o predecessor de cada nó para armezar o menor caminho, além da menor distância
-
Podemos usar uma Heap para encontrar o vértice de menor distância mais rapidamente.
-
A Heap armazena os nós, de acordo com a distância conhecida até o momento.
Algorithmo de Dijkstra
Algorithmo de Dijkstra
Algorithmo de Dijkstra
Algorithmo de Dijkstra
Algorithmo de Dijkstra
Algorithmo de Dijkstra
Algorithmo de Dijkstra
Algorithmo de Dijkstra
Algorithmo de Dijkstra
Algorithmo de Dijkstra
Algorithmo de Dijkstra

Algorithmo de Dijkstra
- É muito parecido com o algoritmo de Prim
- Prim: Encontra uma árvore geradora mínima conectando todos os nós do grafo
- Dijkstra: Encontra uma árvore de menor distância entre um certo nó i para todos os outros nós do grafo
- Complexidade de ambos é similar
Algorithmo de Dijkstra
- Usado na prática
- O protocolo OSPF (Open Shortest Path First), um protocolo de rotamento para redes IP, usa dijkstra
Algorithmo de Dijkstra
- No entanto, o algoritmo tem algumas limitações:
- Os pesos não podem ser negativos
- Se os pesos mudam, o algoritmo precisa ser executado novamente
- No OSPF, um vértice faz broadcast de qualquer mudança para a rede, e então cada vértice executa Dijkstra novamente do zero.
Por que funciona?
- Seja s o nó fonte
- Teorema: Após a execução do algoritmo de Dijkstra, v.distancia é o valor correto de distGw(s,v)
- Observe que:
- Para tovo v∈V(G), v.distancia≥distGw(s,v). Ou seja, nunca subestimamos distGw(s,v)
- Sempre pegamos o mínimo entre o valor atual e um outro caminho com mais uma aresta
- Quando um vértice é "finalizado", v.distancia=distGw(s,v)
- Por contradição, podemos provar que caso contrário, teríamos chegado a v por um caminho de menor distância
- Para tovo v∈V(G), v.distancia≥distGw(s,v). Ou seja, nunca subestimamos distGw(s,v)
Algorithmo Bellman-Ford
- Mais lento que Dijkstra
- Entretanto, pode trabalhar com pesos negativos
- É útil como subrotina de outros algoritmos
- Também tem alguma flexibilidade com relação a mudança de pesos
Algorithmo Bellman-Ford
-
Ideia básica:
- Ao invés de (gulosamente) atulizar apenas o vértice u de menor distância, atualizamos todos os vértices simultaneamente
-
Para melhorar o desempenho, podemos usar programação dinâmica!
Algorithmo Bellman-Ford
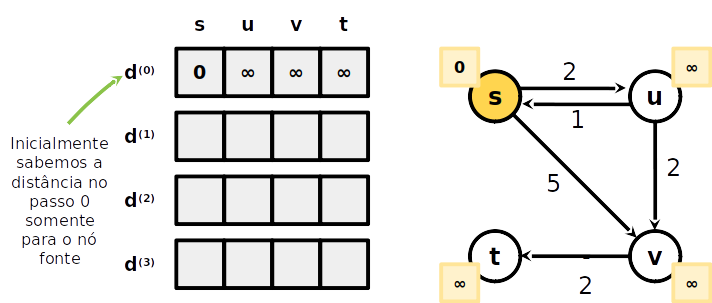
Algorithmo Bellman-Ford
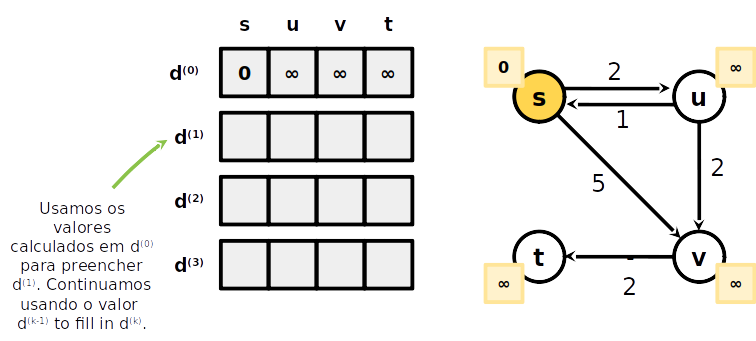
Algorithmo Bellman-Ford
-
Como podemos utilizar as distância d(k−1) calculadas na iteração k−1 para calcular a distância d(k) da iteração k?
-
No passo k, d(k) armazenada a menor distância em no máximo k arestas a partir da fonte
-
Temos dois casos (próximos slides):
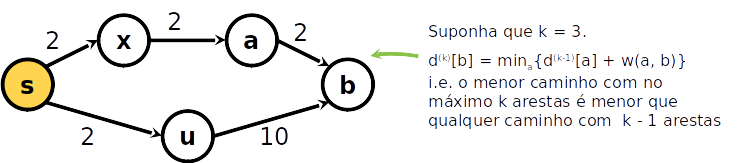
d(k)[b]=min{caso 1d(k−1)[b],caso 2amin{d(k−1)[a]+w(a,b)}}
-
Algorithmo Bellman-Ford
- Caso 1: o menor caminho de s até um nó b com no máximo k arestas tem k−1 arestas, nesse caso
d(k)[b]=d(k−1)[b]
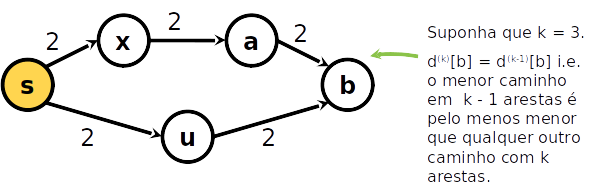
Algorithmo Bellman-Ford
- Caso 2: o menor caminho de s até um nó b tem k arestas
d(k)[b]=amin{d(k−1)[a]+w(a,b)}
Algorithmo Bellman-Ford
Algorithmo Bellman-Ford
Algorithmo Bellman-Ford
Algorithmo Bellman-Ford
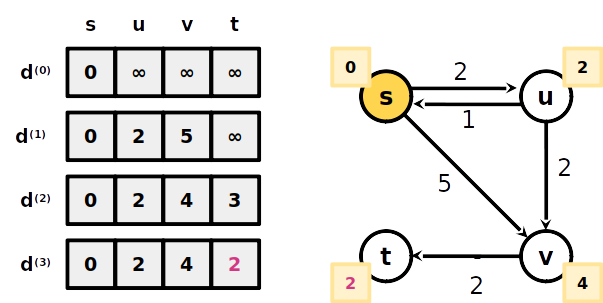
Algorithmo Bellman-Ford
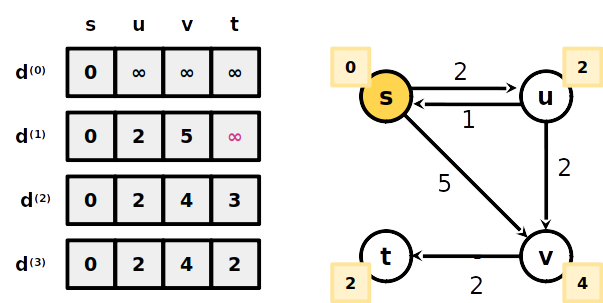
Algorithmo Bellman-Ford
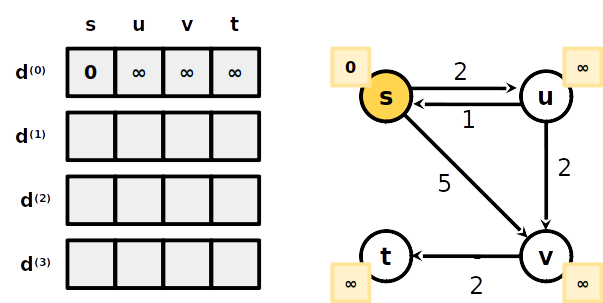
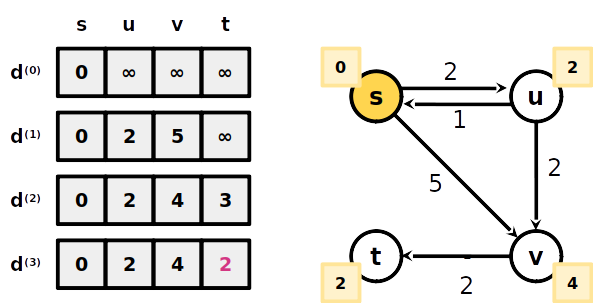
- A menor distância de s a t com no máximo 1 aresta é ∞, portanto não existe um caminho até ele com 1 aresta
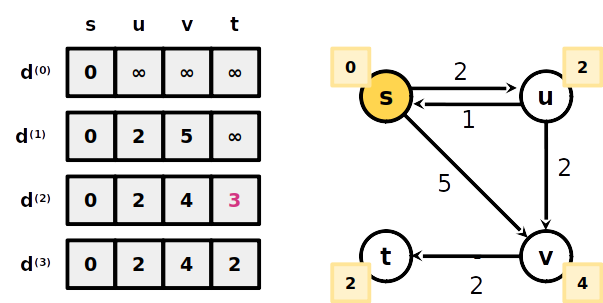
Algorithmo Bellman-Ford
-
A menor distância de s a t com no máximo 1 aresta é ∞, portanto não existe um caminho até ele com 1 aresta
-
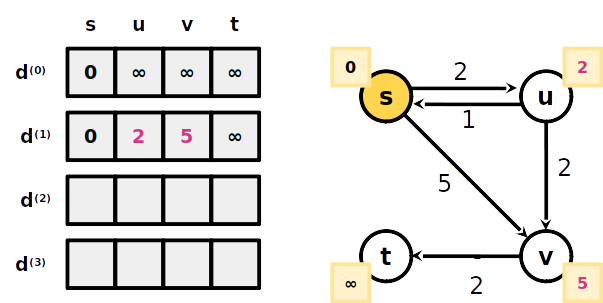
A menor distância de s a 2 com no máximo 2 arestas é 3 (s-v-t)
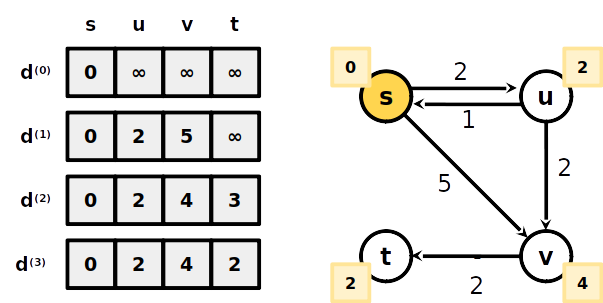
Algorithmo Bellman-Ford
-
A menor distância de s a t com no máximo 1 aresta é ∞, portanto não existe um caminho até ele com 1 aresta
-
A menor distância de s a t com no máximo 2 arestas é 3 (s-v-t)
-
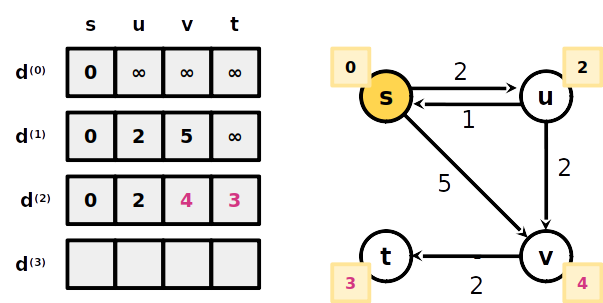
A menor distância de s a t com no máximo 3 arestas é 3 (s-u-v-t)
Por que funciona?
-
Ao final da execução, temo d(∣V∣−1)[b], que é o custo de s a v∈V(G) contendo até ∣V∣−1 arestas.
-
O algortimo estará correto se d(∣V∣−1)[b]=distGw(s,v)
-
Afirmação: Desde que não haja um ciclo negativo, d(∣V∣−1)[b]=distGw(s,v).
Por que funciona?
- Cao o ciclo seja positivo (ou seja, a soma dos pesos das arestas do ciclo vor maior que zero), percorrer o ciclo aumenta o caminho, então ele não está no caminho mínimo
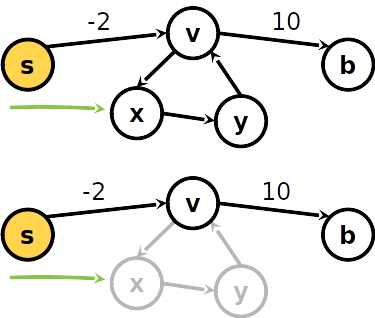
- Um caminho sem ciclos em um grafo com ∣V∣ vértices tem no máximo V−1 arestas.
Ciclos negativos
- Se houver algum ciclo negativo no grafo, haverá alguma aresta u,v tal que
v.distancia>u.distancia+w(u,v) - O que não pode ocorrer se o grafo não tiver um ciclo negativo
Algorithmo Bellman-Ford

Complexidade
- Para cada vértice do grafo, o algoritmo itera (no pior caso) sobre todas as arestas
- Então a sua complexidade é O(∣V∣∣E∣)
Caminho mais Curto entre todos os pares
Dados um grafo G=(V,E) e uma função w de peso nas arestas, calcular distGw(u,v) para todo par u,v∈V(G).
Caminho mais Curto entre todos os pares
-
Uma solução simples seria executar o algoritmo de Bellman-Ford usando cada um dos vértices como fonte
-
Tempo de execução O(∣V∣2∣E∣)
-
Podemos fazer melhor?
Algoritmo de Floyd-Warshall
- Vamos manter uma matrix D(k) de tamanho ∣V∣×∣V∣ para cada k∈[0..∣V∣]
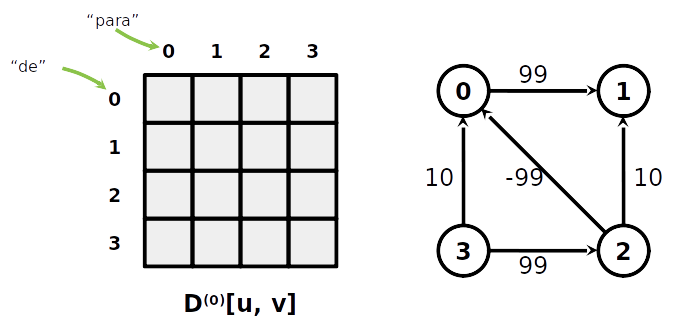
Algoritmo de Floyd-Warshall
- Vamos manter uma matrix D(k) de tamanho ∣V∣×∣V∣ para cada k∈[0..∣V∣]
- D(k)[u,v] é o caminho de u a v, tal que os vértices internos no caminho estão no conjunto {0,...,k−1}
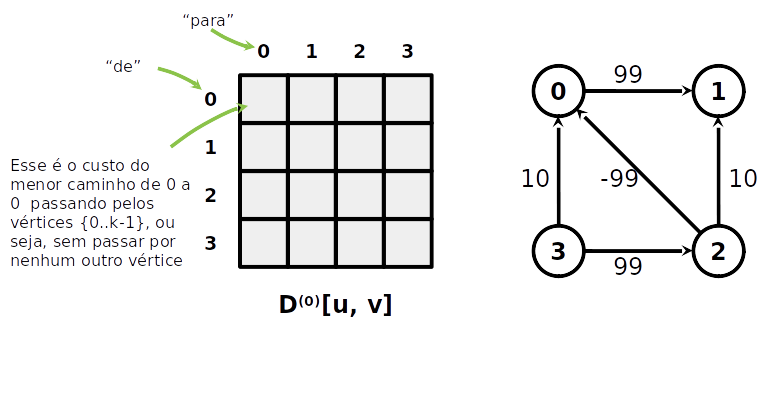
Algoritmo de Floyd-Warshall
- Vamos manter uma matrix D(k) de tamanho ∣V∣×∣V∣ para cada k∈[0..∣V∣]
- D(k)[u,v] é o caminho de u a v, tal que os vértices internos no caminho estão no conjunto {0,...,k−1}
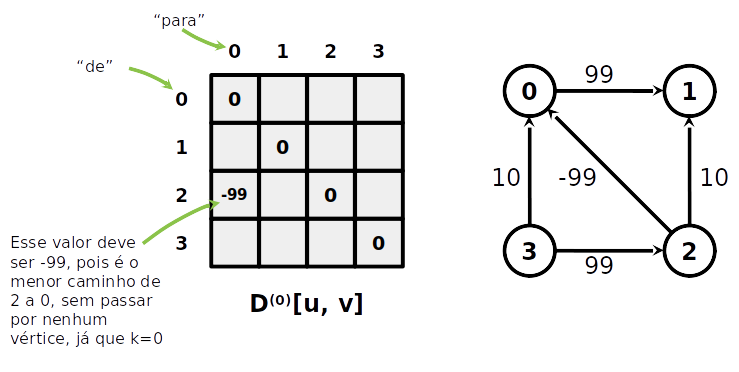
Algoritmo de Floyd-Warshall
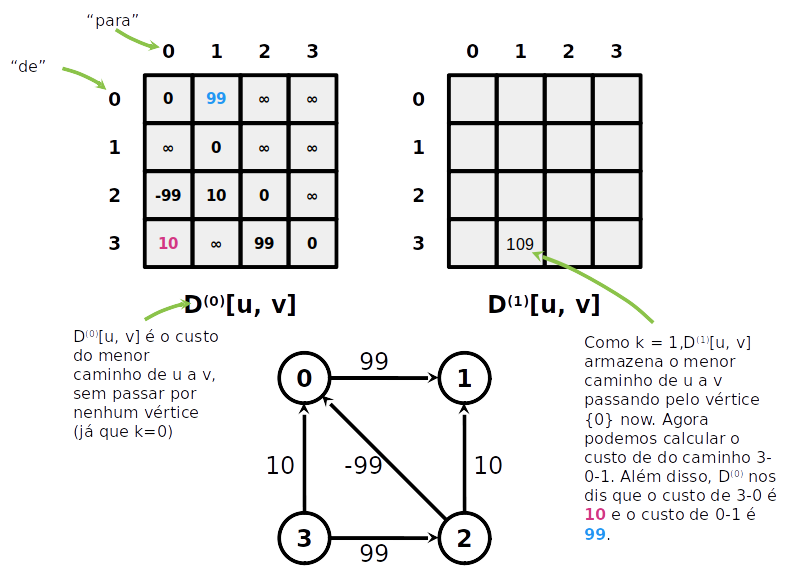
Algoritmo de Floyd-Warshall
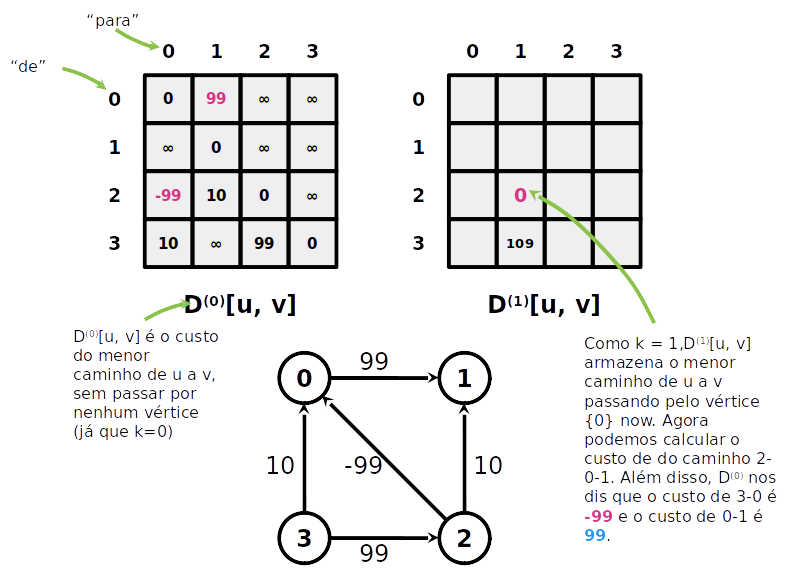
Algoritmo de Floyd-Warshall
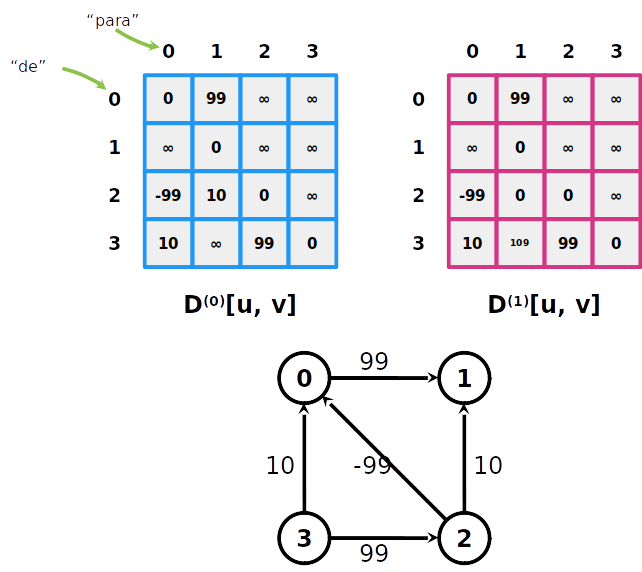
Algoritmo de Floyd-Warshall
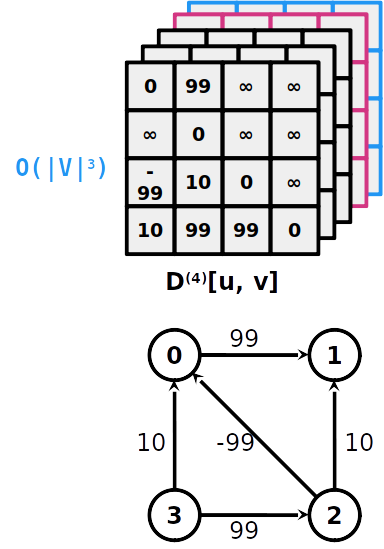
Como atulizar os pesos?
- A cada passo k, temos que D(k)[u,v] é o caminho de u a v, tal que os vértices internos no caminho estão no conjunto {0,...,k−1}
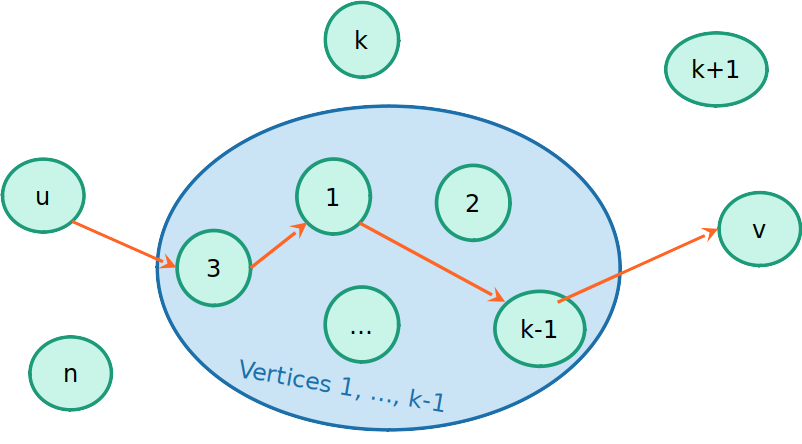
Como atulizar os pesos?
- Para atulizar a matriz no passo k+1, temos dois casos:
- O caminho mais curto passa pelo vértice k
- O caminho mais curto não passa pelo vértice k
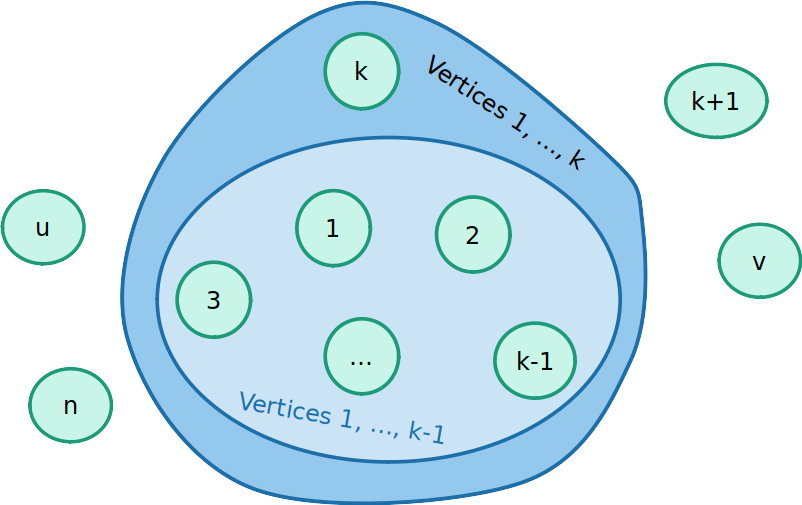
Como atulizar os pesos?
- Caso 1: O caminho mais curto passa pelo vértice k
D(k)[u,v]=D(k−1)[u,v]
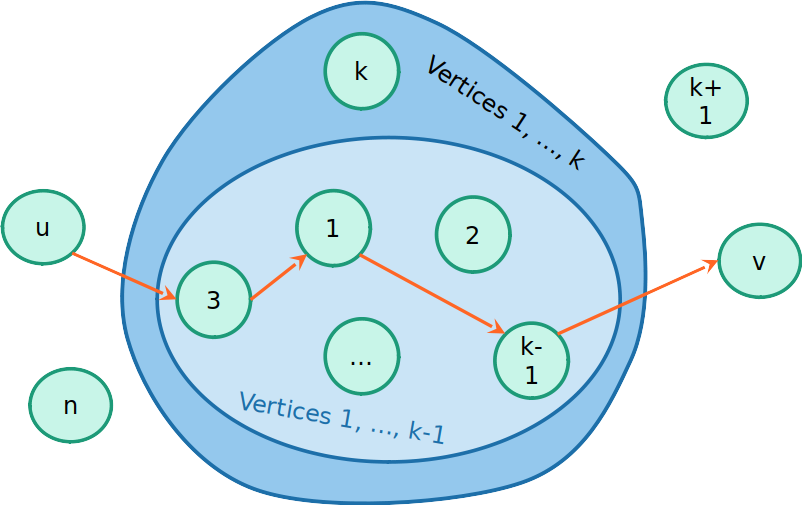
Como atulizar os pesos?
- Caso 2: O caminho mais curto não passa pelo vértice k
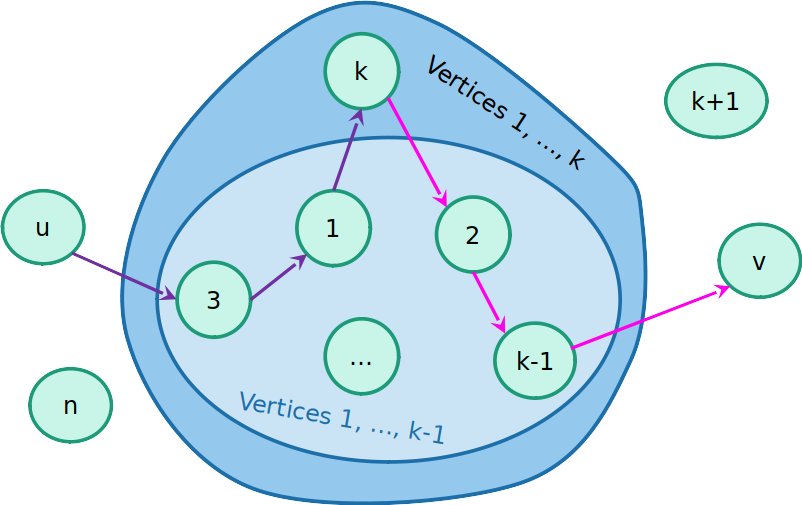
D(k)[u,v]=D(k−1)[u,k]+D(k−1)[k,v]
Como atulizar os pesos?
- Combinando os dois casos, temos:
D(k)[u,v]=min{D(k−1)[u,v],D(k−1)[u,k]+D(k−1)[k,v]}
Algoritmo de Floyd-Warshall

Algoritmo de Floyd-Warshall
- É fácil ver que a complexidade do algoritmo é O(∣V∣3)
Resumo
| Algoritmo | Dijkstra | Bellman-Ford | Floyd-Warshall |
|---|---|---|---|
| Problema | caminho mínimo de única fonte | caminho mínimo de única fonte | caminho mínimo para todos os pares |
| Complexidade | O((∥V∥+∥E∥)log∥E∥) (usando Heap) | O(∥V∥∥E∥) | O(∥V∥³) |
| Vantagens | Funciona com arestas de pesos negativos, e pode detectar ciclos negativos | Funciona com arestas de pesos negativos, e pode detectar ciclos negativos | |
| Desvantagens | Pode não funciona com arestas de pesos negativos | ||
| Tipo | Guloso | Programação Dinâmica | Programação Dinâmica |