Tipos de problemas

• Problema de decisão, em que a resposta é sim ou não
• Problema de busca, em que queremos encontrar uma solução satisfazendo algumas propriedades se ela existir. Caso contrário, retornar que não exite
• Problema de otimização, em que cada solução tem um valor associado, e queremos encontrar uma solução com o melhor valor (máximo ou mínimo)

Tratabilidade

• Intuição:

  • Problema é tratável se existem algoritmos eficientes para ele
  • Problema é intratável se tais algoritmos não existem

• Até agora no curso, praticamente todos os problemas que encaramos eram tratáveis

• Mas nada garante que seja sempre este o caso

Algoritmo eficiente

• Definição clássica de eficiência:

  • Um algoritmo é eficiente se e somente se ele executa em tempo polinomial em um computador serial

• Se o grau do polinômio for grande, o problema deve ser inviável

  • $O(n)$, $O(n \log n)$, $O(n^2 \log^2 n)$ - ok!
  • $O(n^{10.000.000.000})$ - eficiente?

• Tempo de execução exponencial podem ser eficientes na prática

  • $O(2^n)$, $O(n!)$ - ok!
  • $O(1.0000000001^n)$ - ineficiente?

Tratabilidade

• Um problema é chamado de tratável se e somente se existe um algoritmo eficiente (isto é, de tempo polinomai) que o revolsa.

• Um problema é chamado de intratável se e somente se não existe um algoritmo eficiente que o resolva.

• Problemas intratáveis são comuns. Precisamos reconhecê-los quando nos deparamos com algum deles na prática.

A classe de complexidade P

• P é a classe dos problemas resolvidos em tempo polinomial
• Exemplos de problemas em P:
  • Caminho mais curto
  • Ordenação
  • Árvore geradora mínima
  • Fluxo em redes
  • Multiplicação de matrizes

A classe de complexidade P

• Infelizmente, nem todo problema está em P 😦
• Existem problemas para os quais não existe qualquer algoritmo
  Ex. problema da Parada
• Existem outros para os quais, por mais que se busque, não sãoconhecidos algoritmos polinomiais
  Ex.: problema do Caixeiro Viajante (TSP)
• Mas, a princípio, isso não garante que tais algoritmos não existam
• Como descrever uma classe que englobe problemas como o TSP?

A classe de complexidade NP

• A classe NP consiste em todos os problemas de decisão em que podemos verificar se uma solução é correta em tempo polinomial

• Essas definições são algorítmicas

• Definiçõeses formais destas classes vem da área de teoria da computação

• O nome NP significa "Nondeterministic Polynomial"

A classe de complexidade NP

• Todo problema em NP é resolvével usando busca por força bruta

  • O espaço de busca é no máximo exponencial, e cada solução pode ser testada em tempo polinomal

• Exemplos:

  • Satisfatibilidade (SAT)
  • Cobertura por Vértices
  • Problema do Caixeiro Viajante (TSP)

P e NP

• Situação dos problemas

  • Temos problemas em P, que também estão em NP (por que?)
  • Temos problemas em NP, que não sabemos se estão em P

• Muitos problemas importantes na segunda situação

• Como corroborar a dificuldade destes problemas?

  • Vamos utilizar evidências relativas, usando:
    • Redução
    • Completude

Redução

• O problema $A$ se reduz ao problema $B$ se conseguimos resolver qualquer instância de $A$ usando um algoritmo que resolve $B$

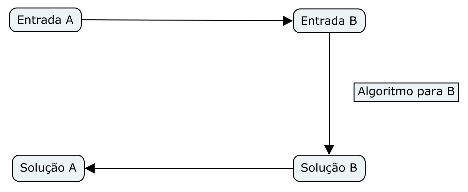
• Transformamos a entrada $A$ em entrada $B$, e depois a solução $B$ em solução $A$
• Se transformações são polinomiais, $A$ é polinomialmente redutível a $B$

Redução

• Exemplo: Seleção em Ordenação. Vamos usar um algoritmo de ordenação para selecionar o $k$-ésimo menor elemento de de um vetor

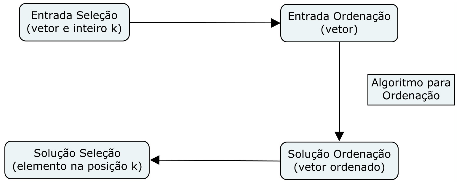
• Esta reduçãoo resolve o problema da seleção em tempo $O(n \log n)$
• Note que é possível resolver a seleção em tempo linear

Redução

• Numa redução o algoritmo para $B$ pode ser utilizado várias vezes
• Exemplo: Caminho Todos para Todos em Caminho Um para Todos

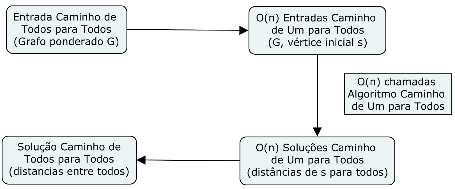
• Notem que nesse caso o algoritmo obtido ainda é polinomial

Redução

• Reduçãoo entre problemas é uma técnica valiosa para o projeto de algoritmos
• Permite utilizar soluções já conhecidas para resolver novos problemas
• Um projetista de algoritmos sempre deve se perguntar:

“Será que este problema não se parece com algum que eu já conheço?”

Redução

• Redução usada para atestar a dificuldade relativa de um problema
• Como provar que um problema é tão difícil quanto outro?

• Observe que $B$ não pode ser mais fácil do que A

Clique-k

• Dados um grafo $G$ e um inteiro positivo $k$, existe conjunto $S\subseteq V(G)$ de vértices tais que para todo par $u,v \in S$ existe uma aresta $uv \in E(G)$ (S é clique) e $|S|\geq k$?

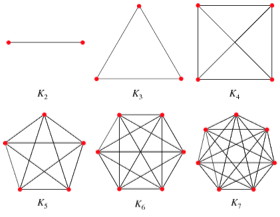
• Clique-k está em NP:
  • É um problema de decisão (a resposta é sim caso exista)
  • Dados $G$, $k$ e $S$ É fácil verificar se $S$ é uma clique: basta verificar se todos os pares de vértices formam arestas e contar os vértices de $S$

$k$-Cobertura por vértices

• Dado um grafo $G$ e um inteiro $k$, existe conjunto $S\subseteq V(G)$ tal que, para toda aresta $uv \in E(G)$, $u \in S$ ou $v \in S$ e $|S|\leq k$?

• $k$-Cobertura por vértices está em NP pois, dados $G$, $k$, e $S$ podemos verificar em tempo polinomial se $|S|\leq k$ e se todas as arestas do grafo tem ao menos uma aresta no conjunto.

Redução

• Exemplo: Clique-k é redutivel para k-cobertura por vértices

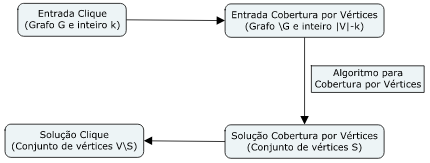
• Se clique-k não tiver um algoritmo polinomial
• Então k-cobertura por vértices também não tem um algoritmo de tempo polinomial

Redução

• Exemplo: Clique-k é redutivel para k-cobertura por vértices

  • O complemento $G_c$ de um grafo $G$ contém exatamente as arestas que não estão em $G$
  • Podemos calcular $G_c$ em tempo polinomial
  • $G$ tem uma clique de tamanho $k$ se e somente se $G_c$ tem uma k-cobertura de tamanho $|V|-k$

Redução

• Exemplo: Clique-k é redutivel para k-cobertura por vértices

• Afirmação: Se $G$ tem um clique de tamanho $k$, $G_c$ tem uma k-cobertura de tamanho $|V|-k$

  • Seja $V'$ uma clique
  • Então $V-V'$ é uma cobertura por vértices em $G_c$
    • Seja $(u,v)$ qualquer vértice em $G_c$
    • Então $u$ e $v$ não podem estar ambos em $V'$
    • E pelo menos $u$ ou $v$ está $V-V'$, então a aresta $(u,v)$ é coberta por $V-V'$
    • Já que isso é valido para qualquer aresta em $G_c$, $V-V'$ é uma cobertura por vértices

Redução

• Exemplo: Clique-k é redutivel para k-cobertura por vértices

• Afirmação: Se $G$ tem um clique de tamanho $k$, $G_c$ tem uma k-cobertura de tamanho $|V|-k$

  • Para todo $u,v \in V$, se $(u,v) \in G_c$, então $u\in V'$ ou $v\in V'$, ou ambos
  • Caso não fosse verdade, $(u,v) \in E(G)$
  • Em outras palavras, todos os vértices de $V-V'$ estão conectados por uma aresta, então $V-V'$ é uma clique
  • Uma vez que $|V|-|V'|=k$, o tamanho da clique é $k$

Exemplo

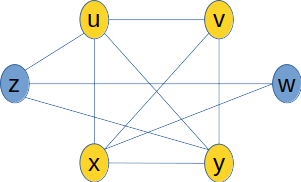
• $G$ possui uma clique $V'$ de tamanho $k$

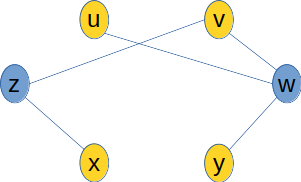
• $G_c$ possui uma cobertura por vértice $V\setminus V'$ de tamanho $n-k$

Redução

• Interpretaçõees para “A é redutível a B”:

  • "Positiva" $A$ ́e no máximo tão difícil quanto $B$
  • "Negativa" $B$ ́e pelo menos tão difícil quanto $A$

• Primeira expande o conjunto de problemas tratáveis

• Segunda expande o conjunto dos intratáveis

Completude

• Um Problema $\Pi$ é $C$-Completo se:

  • $\Pi$ está em $C$
  • Todo problema em $C$ é redutível a $\Pi$

• Podemos pensar que $\Pi$ é o "problema mais difícil" em $C$

• Notem quão forte é essa definição

• E que não é tão óbvio que algum problema $\Pi$ em $C$ a satisfaça

Completude

• Apesar disso, vamos supor que existam problemas $C$-Completos

• Sendo $\Pi$ um problema em $C$

• Para mostrar que $\Pi$ ́e $C$-Completo temos que:

  • Escolher um problema $C$-Completo $\Pi'$
  • Reduzir o problema $\Pi'$ para $\Pi$

• Isso funciona pois:

  • Todo problema em $C$ é redutível a $\Pi'$
  • E por consequência é redutível a $\Pi$

Completude

• Voltamos à questão:

  "Como mostrar a dificuldade dos problemas em NP (que não sabemos se estão em P)?”

• Um forte atestado de dificuldade seria mostrar que todo problema de $NP$ reduz pra um desses problemas

• Já que isso mostraria que esse problema e o mais difícil dentre todosde $NP$ e que bastaria resolver ele pra resolver todos os outros

• Mas, será que a classe dos problemas NP-Completos é ou não vazia?

Completude

• Por incrível que pareça, existem muitos problemas $NP$-Completos
• Sendo um exemplo notável o problema da satisfatibilidade (SAT)
• Já sabemos que para mostrar que um problema é NP-Completo, basta reduzir qualquer problema $NP$-Completo a ele
• Assim, muitos outros problemas foram provados $NP$-Completos

Satisfatibilidade

• Considere um conjunto de variáveis booleanas $x_1, x_2, \cdots, x_n$
• E uma fórmula composta por essas variáveis e conjunçẽos (operador e) de conjuntos de disjunções (operadores ou). Por exemplo:

$\left(x_{1} \vee \overline{x_{2}} \vee \overline{x_{3}} \vee x_{4}\right) \wedge\left(\overline{x_{1}} \vee x_{2}\right)$

$\left(x_{1} \vee \overline{x_{2}} \vee \overline{x_{3}}\right) \wedge\left(\overline{x_{1}} \vee x_{2} \vee x_{4} \vee x_{5} \vee \overline{x_{6}}\right)$

• Cada conjunto de disjunção é chamado de cláusula.
• Um literal é uma variável $x$ ou sua negação $\overline{x}$
• O problema da satisfatibilidade consiste em verificar se a fórmula é satisfatível, isso é, existe uma atribuição de valores para as variáveis tal que a fórmula tem o valor 1.

3-SAT

• Uma fórmula booleana formada por conjunções de cláusulas que contém exatamente 3 literais é chamado de 3-CNF. Por exemplo

$\left(x_{1} \vee \overline{x_{2}} \vee \overline{x_{3}}\right) \wedge\left(\overline{x_{1}} \vee x_{2} \vee x_{4}\right)$
$\left(x_{1} \vee \overline{x_{2}} \vee \overline{x_{3}}\right) \wedge\left(\overline{x_{1}} \vee x_{2} \vee x_{4}\right) \wedge\left(\overline{x_{4}} \vee x_{5} \vee \overline{x_{6}}\right)$

• O problema 3-SAT consiste em verificar se uma fórmula 3-CNF é satisfatível, ou seja, se existe uma atribuição de valores para as variáveis tal que a fórmula 3-CNF tenha valor 1.

3-SAT é NP-completo

• Observe que 3-SAT está em $NP$ pois dada uma fórmula e uma atribuição das variáveis, é fácil verificar se essa atribuição satisfaz a fórmula

• Em 1972, Stepehn Cook e Richard Karp provaram que 3-SAT é NP-completo.

• Hoje em dia, se conhecem milhares de problemas que são NP-Completos

3-SAT é redutível para Clique-k

• Dada uma fórmula 3-CNF $\phi$ com $k$ cláusulas sobre as variáveis $x_1, x3, \cdots, x_n$

• Construímos um grafo $G$ que possui $3k$ vértices, de modo que cada cláusula tem 3 vértices representando cada um de suas variáveis.

• Um par de vértices $v$ e $w$ de $G$ forma uma aresta se e somente se $v$ e $w$ estão em cláusulas diferentes, $v$ corresponde a um literal $x$
  e $w$ não corresponde a um literal $\overline{x}$

3-SAT é redutível para Clique-k

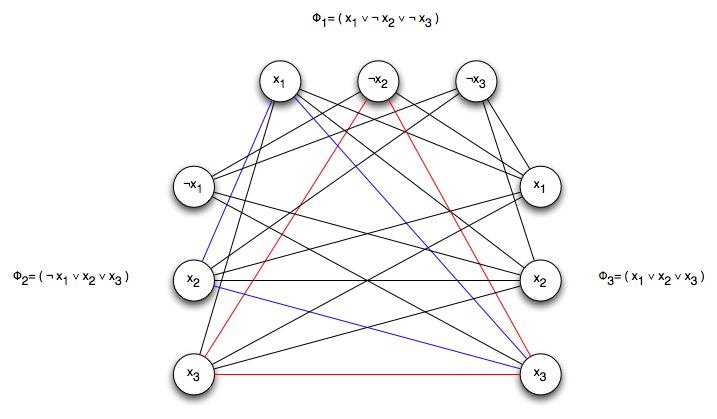
3-SAT é redutível para Clique-k

• $\phi$ com $k$ clausulas é satisfatível se e somente se existir um clique-k no grafo $G$

• Se existir uma clique em $G$, então existe $\phi$ é satisfatível

  • Por definição, uma clique-k implica que existe $k$ vértices em $G$ que são conecatados entre si.
  • Pela nossa construção, o fato que dois vértices estão conectados entre si significa que eles podem receber uma atriuição consistente (podemos atribuir 1 a todos eles), e eles estão em cláusulas diferentes
  • Uma vez que existem $k$ vértices na clique, então pelo menos uma literal em cada uma das $k$ cláusulas podem ser atribuídas a 1, isto é, $\phi$ pode ser satisfeita.

3-SAT é redutível para Clique-k

• $\phi$ com $k$ clausulas é satisfatível se e somente se existir um clique-k no grafo $G$

• Se $\phi$ pode ser satisfeita, então existe uma clique em $G$

  • Se $\phi$ pode ser satisfeita, então pelo menos uma literal em cada cláusula é atribuída ao valor 1
  • Considere os vértices correspondentes a essas literais. Uma vez que as literais são consistentes e elas estão em diferentes cláusulas, existe uma aresta entre cada par delas.
  • Uma vez que existem $k$ cláusulas em $\phi$, temos um subconjunto de tamanho de pelo menos $k$ vértices no grafo com arestas entre cada par de vértices, isto é, uma clique-k em G.

NP-Completude

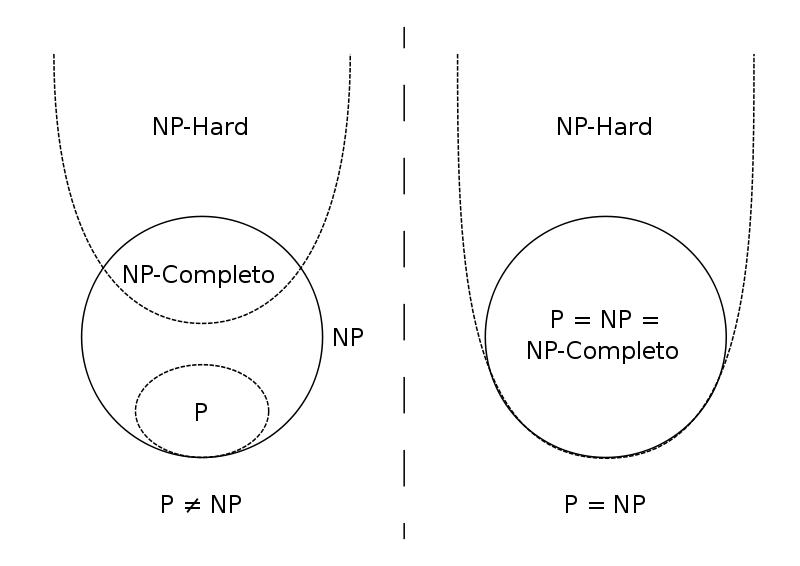
$P \stackrel{?}{=} NP$

• O problema $P \stackrel{?}{=} NP$ é um problema classico

• Se existir algoritmo polinomial para um problema NP-Completo...

• conseguimos resolver todos os problemas em $NP$ em tempo polinomial, provando que $P=NP$...

• e respondendo assim à maior questão em aberto da ciência da computação.

• Entretanto, muitos pesquisadores acreditam que isso não é possível, mas não se conhece uma prova que $P\neq NP$

Problemas $NP$-completos

• A ligação entre $NP$-Completude e a questão $P \stackrel{?}{=} NP$ demonstra a importância desta classe para a ciência da computação
• Mas por que um projetista de algoritmos deveria se preocupar?
• Porque problemas $NP$-Completos são extremamente comuns
• E existe pouca esperança de obter um algoritmo polinomial para eles

Problema $NP$-difícil

• $NP$-difícil é o conjunto de problemas $Q$ tais que todo outro problema de $NP$ é redutível a $Q$

• O problema $Q$ é pelo menos tão difícil quanto qualquer outro problema em $NP$

• O problema $Q$ não precisa estar em $NP$, pois não precisa ser um problema de decisão.

• Uma outra definição para $NP$-Completo são os problemas NP que são $NP$-difíceis.

Problema $NP$-difícil

• Se $P \neq NP$, então não existe solução polinomial para os problemas $NP$-Hard

Problemas $NP$-completos

• Assim, se voce se deparar com um problema difícil
• É importante saber verificar se ele é NP-Completo ou $NP$-Difícil
• Para tratá-lo de modo adequado
• Hoje não apresentamos opções para lidar com problemas $NP$-Completos
• Mas mostramos como identificá-los