Ordenação

• Algortimos de ordenação ordenam uma sequência de valores
  • vamos assumir por enquanto que os valores a serem ordenados são todos distintos entre si.

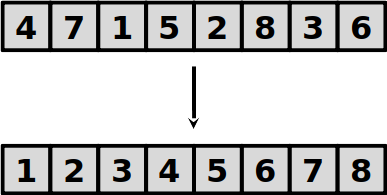
Ordenação por inserção

• Dado um vetor $A$ com $n$ números, a ordenação por inserção irá executar $n$ rodadas de instruções em que:
• A cada rodada, temos um subvetor de $A$ ordenado que contém um elemento a mais do que o subvetor da rodada anterior:
  • Ao fim da $i-1$-ésima rodada, o subvetor $A[1..i-1]$ estará ordenado
• Sabendo que o $A[1..i-1]$ está ordenado, é fácil encaixar o elemento A[i] na posição correta, para deixar o subvetor $A[1..i]$ ordenado:
  • Seja $atual = A[i]$. Iterativamente troque o elemento $atual$ com os anteriores enquanto eles forem maiores que $atual$.

Ordenação por inserção

• Algoritmo InsertionSort
  

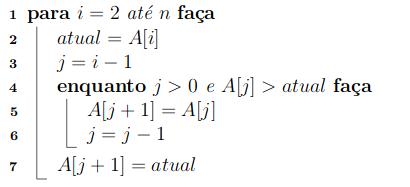
Ordenação por inserção

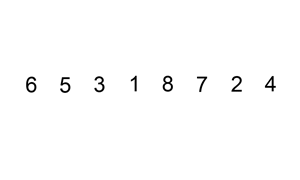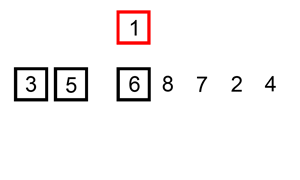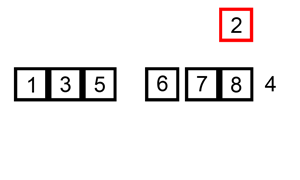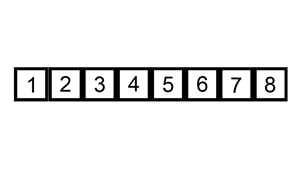
Ordenação por inserção

Uma possível implementação em Python

def insertion_sort(A):
  for i in range(1, len(A)):
    atual = A[i]
    j = i - 1
    while j >= 0 and A[j] > atual:
      A[j+1] = A[j]
      j -= 1
    A[j+1] = atual

(observe que em Python a posição inicial do vetor é 0, então os índices foram ajustados adequadamente.)

Análise do InsertionSort

• Vamos reponder as três perguntas com relação a análise de algoritmos:
  1. O algoritmo está correto?
  2. Quantos recursos o algoritmo consome?
  3. É possível fazer melhor?

Corretude do InsertionSort

• Algoritmos frequentemente inicializam, modificam, apagam ou inserem novos dados

  • Existe uma maneira de provar que o algoritmo funciona, sem checar (as infinitas) entradas?

• Ideia principal: encontrar um invariante.

  • para raciociar sobre o comportamento de um algoritmo, frequentemente é útil identificar coisas que não mudam.

Invariante do InsertionSort

• Suponha que temos o vetor $[1,2,3,5,6,7,8|\mathbf{4}]$, em que o subvetor $[1,2,3,5,6,7,8]$ já está ordenado e o elemento atual é o $\mathbf{4}$.
• Iserir o $\mathbf{4}$ imediatamente à direita do maior elemento do subvetor que é menor que $\mathbf{4}$ (isto é, à direita de $3$) produz um outro vetor ordenado.
• Observe que este novo vetor é mais longo que o anterior por um elemento: $A=[1,2,3,\mathbf{4},5,6,7,8]$

Invariante do InsertionSort

• Podemos aplicar essa ideia a cada passo:

  • $[6|,\mathbf{5},3,1,8,7,2,4]$: o subvetor $[6]$ está ordenado. Inserir o $\mathbf{5}$ na posição correta gera um subvetor ordenado $[5,6]$
  • $[5,6|,\mathbf{3},1,8,7,2,4]$: o subvetor $[5,6]$ está ordenado. Inserir o $\mathbf{3}$ na posição correta gera um subvetor ordenado $[3,5,6]$
  • $[3,5,6,|\mathbf{1},8,7,2,4]$: o subvetor $[3,5,6]$ está ordenado. Inserir o $\mathbf{1}$ na posição correta gera um subvetor ordenado $[1,3,5,6]$
  • $\cdots$
  • $[1,2,3,5,6,7,8|\mathbf{4}]$: o subvetor $[1,2,3,5,6,7,8]$ está ordenado. Inserir o $\mathbf{4}$ na posição correta gera um subvetor ordenado $[1,2,3,4,5,6,7,8]$

Corretude do InsertionSort

• Existe um nome para a condição que é verdadeira antes e depois de cada iteração de um laço: invariante de laço

• Para provar a corretudo do InsertionSort, vamos usar o invariante de laço e fazer uma prova por indução

• Nesse caso, o invariante de laço é que, ao início da iteração $i$ (a interação que queremos inserir o elemento $A[i]$ no subvetor ordenado), o subvetor $A[1..i-1]$ está ordenado

Corretude do InsertionSort

• Em uma prova por indução, temos quatro componentes:

  • Hipótese de indução: o invariante de laço é verdadeiro depois da $i$-ésima iteração

  • Caso base: o invariante de laço é verdadeiro na primeira iteração.

  • Passo de indução: se o invariante de laço é verdadeira dapara a $i$-ésima interação, então ele também é verdadeiro para $i+1$-ésima iteração

  • Conclusão: se o invariante de laço é veradeira após a última iteração, então o algoritmo está correto!

Corretude do InsertionSort

• Especificamente para o InsertionSort:

  • Hipótese de indução: na iteração $i$, $A[1..i-1]$ está ordenado

  • Caso base: $A[1]$ está ordenado.

  • Passo de indução: ao inserir o elemento $A[i]$, $A[1..i]$ continua ordenado

  • Conclusão: na $n$-ésima iteração (ao final do algortimo), $A[1..n]$ (portanto o vetor inteiro) estará ordenado.

Corretude do InsertionSort

• O caso base é verdade, pois um sub-vetor de 1 único elemento está ordenado.
• Vamos supor que a hipótese de indução é válida para um $i \in (2..n)$ (isto é, $A[1..i-1]$ está ordenado).
• Enquanto o laço "move" o elemento $atual (A[i])$ para a esquerda, os elementos maiores que $atual$ são movidos uma posição para a direita, e continuam or ordem.

Corretude do InsertionSort

• Quanto $atual$ chega na posição "correta" no subvetor, todos os elementos à direita são maiores e todos os elementos a direta são menores que $atual$. Portanto, $A[1..i]$ está ordenado e a invariante se mantém.
• O laço termina quando $i=n$, portanto $A[1..n]$ está ordenado e contendo todos os elementos do vetor $A$.
• Podemos concluir que o algoritmo está correto.

Quantos recursos o algoritmo consome?

• A quantidade de memória extra é desprezível: só precisamos de espaço extra para armazenar $atual$ (ordenação in place)

• Com relação ao tempo:

  • O laço da linha 1 é executado $n$ vezes. Consequentemente, as linhas 2, 3 e 7 são executadas $n-1$ vezes cada.
  • Seja $r_i$ a quantidade de vezes que o laço da linha 4 é executado para a iteração $i$. As linhas 5 e 6 são executacas $r_i -1$ vezes cada.

Quantos recursos o algoritmo consome?

• Vamos escrever o tempo gasto pelo algoritmo com um polinômio $T(n)$:

  $\begin{aligned} T(n) &= \underbrace{n + 3(n-1)}_{\text{laço externo}}+ \underbrace {\sum_{i=2}^n r_i + 2\sum_{i=2}^n (r_i-1) }_{\text{laço interno}} \\ T(n) &= 4n-2 + 3 \sum_{i=2}^n r_i -2 \sum_{i=2}^n 1 \\ T(n) &= 2n + 3 \sum_{i=2}^n r_i \end{aligned}$

• Para saber quantos recursos o algoritmo consome, precisamos saber o valor de $r_i$.

Quantos recursos o algoritmo consome?

• Melhor caso:

  • se o vetor já estiver odenado, o laço da linha 4 é executado 1 única vez ($r_i =1, \forall i \in 2..n$) para cada iteração.

  $\begin{aligned} T(n) &= 2n + 3 \sum_{i=2}^n r_i \\ &= 5n -3 \end{aligned}$

Quantos recursos o algoritmo consome?

• Pior caso:
  • se o vetor estiver inversamente odenado, o laço da linha 4 é executado $i$ vezes ($r_i =i, \forall i \in 2..n$) para cada iteração.
    $\begin{aligned} T(n) &= 2n + 3 \sum_{i=2}^n r_i \\ &= n^2 + 2n - 6 \end{aligned}$
    (veja a somatório de Gauss para calcular o somatório)

Quantos recursos o algoritmo consome?

• Caso médio:
  - para fazer uma análise do caso médio, precisamos fazer alguma suposição sobre $r_i$. Supunha que, em um caso típico, linha 4 é executada metade das vezes com relação ao pior caso ($r_i =\frac{i}{2}, \forall i \in 2..n$) para cada iteração.

$\begin{aligned} T(n) &= 2n + 3 \sum_{i=2}^n r_i \\ &= 2n + \frac{n(n-1)}{4} \end{aligned}$

Notação assintótica

• O que significa medir o "tempo de execução" de um algoritmo?
  • Engenheiros provavelmente se importam com o "tempo de execução" (wall time): quanto tempo o algoritmo leva em segundos, minutos, horas, etc.
  • Isso depende de características do hardware, implementação, linguagem de programação, etc.
  • Apesar de importante, não será o nosso foco
  • Ao invés, queremos uma medida que é independente dessas considerações.

Notação assintótica

• Ideia principal: focar como o tempo de execução escala em função de $n$ (o tamanho da entrada).
  • Vantagens:
    • Abstrai o hardware, linguagem de programação, etc.
    • Mais genérica que a abordagem de implementar e testar
  • Desvantagens:
    • Só faz sentido se $n$ é grande comparado com as constantes ($9.999.999.999.999 n$ é melhor que $n^2$?)

A notação $O$

• A notação $O$ (big-O) é uma notação matemática para considerar o limite superior para o crescimento de uma função
  • Informalmente, ela pode ser obtida ignorando-se as constantes e termos que não dominam o crescimento da função

A notação $O$

• Seja $T(n)$ e $g(n)$ funções sobre inteiros positivos.

  • Podemos pensar em $T(n)$ como funções de tempo de execução: positiva e crescente em função de $n$.

• Dizemos que "$T(n)$ é $O(g(n))$" se $g(n)$ cresce pelo menos tão rápido quanto $T(n)$ conforme, $n$ cresce.

• Mais formalmente

$T(n) =O(g(n))$ se existem constantes positivas $C$ e $n_0$ tais que $T(n)\leq C g(n)$ para todo $n\geq n_0$;

A notação $O$

• Graficamente:

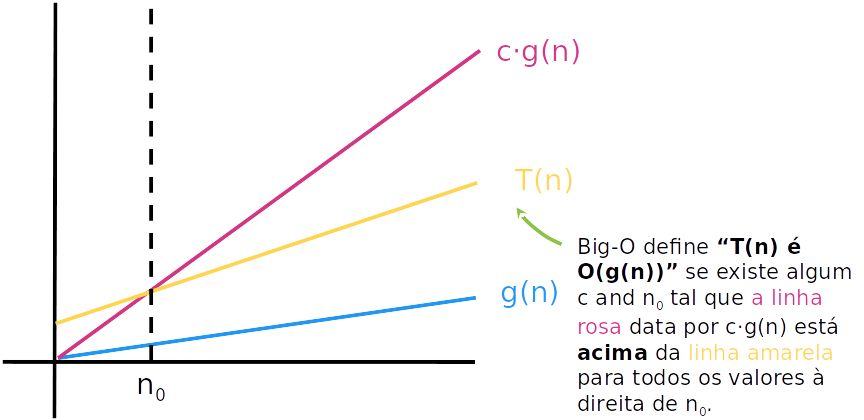
A notação $O$

• Graficamente:

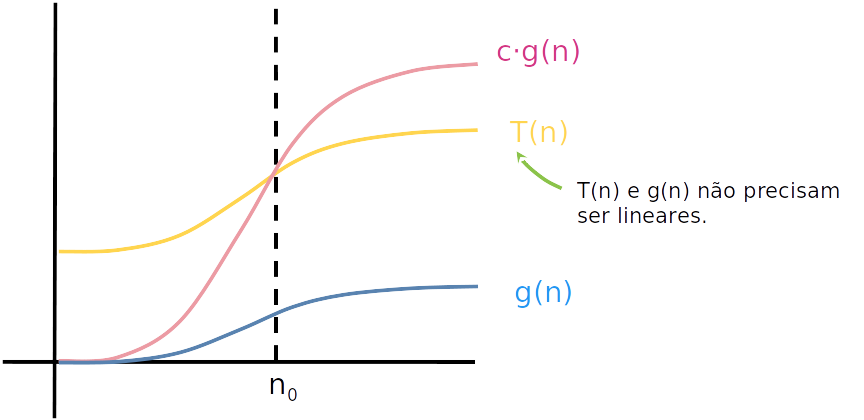
A notação $O$

• Graficamente:

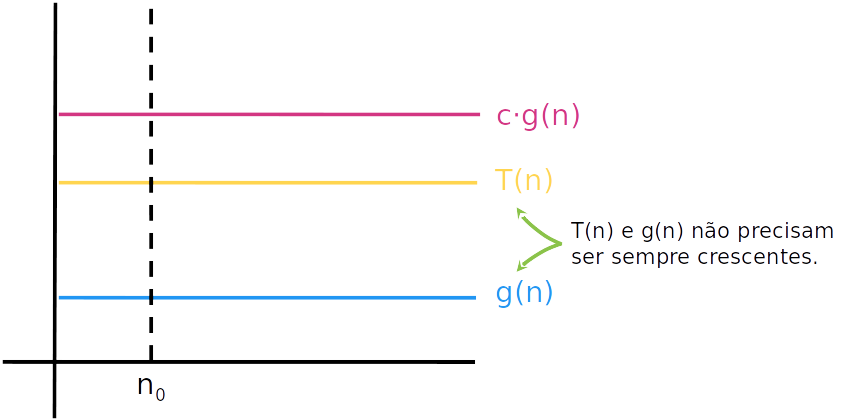
A notação $O$

• Graficamente:

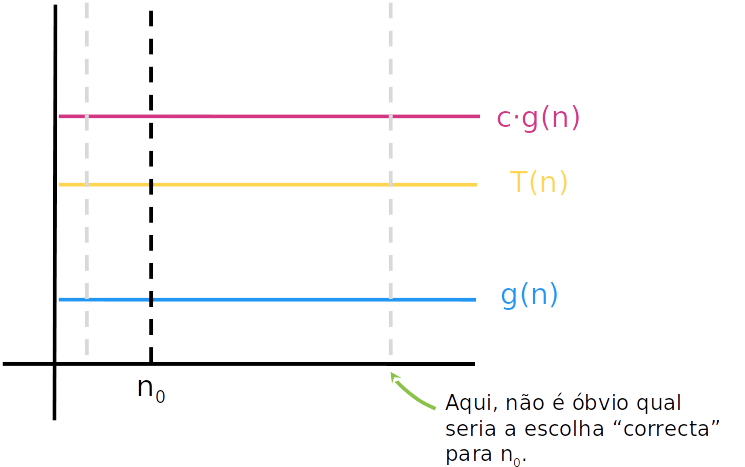
A notação $O$

• Graficamente:

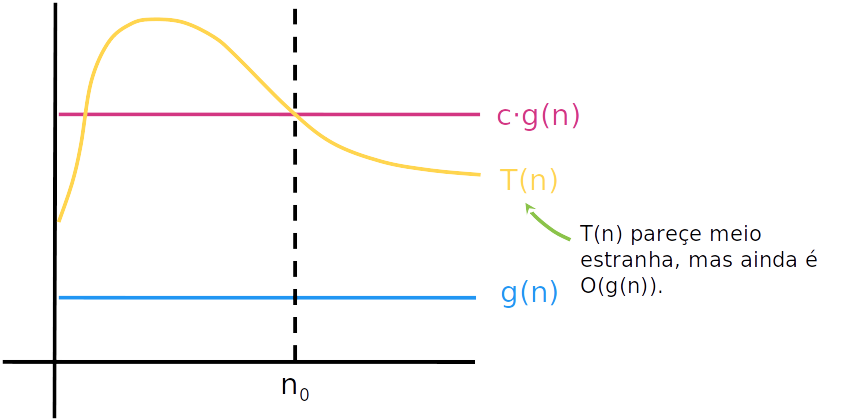
A notação $O$

• Para provar que $T(n) = O(g(n))$, temos que mostrar que existe um $c$ e $n_0$ que satizfaz a definição.

• Por exemplo, queremos provar que $T(n) = 10n^2+ 5n+ 3$ and $g(n) = n^2$. Podemos mostrar que $T(n) = O(g(n))$ encontrando um $c$ e $n_0$ de acordo com a definição. Por exemplo:
  $C = \frac{10n^2+ 5n+ 3}{n^2} = 10 + \frac{5}{n} + \frac{3}{n^2}$
  para $n\geq 1$ temos que
  $10 + \frac{5}{n} + \frac{3}{n^2} \leq 10 + 5 + 3 = 18$

• Basta tomar $n_0=1$ e $C=18$, e temos que $T(n) = O(g(n))$

A notação $\Omega$

• A notação $\Omega$ (big-$\Omega$) é uma notação matemática para considerar o limite inferior para o crescimento de uma função
  • Informalmente, ela pode ser obtida ignorando-se as constantes e termos que não dominam o crescimento da função

A notação $\Omega$

• Seja $T(n)$ e $g(n)$ funções sobre inteiros positivos.

• Dizemos que "$T(n)$ é $\Omega(g(n))$" se $g(n)$ cresce no máximo tão rápido quanto $T(n)$ conforme, $n$ cresce.

• Mais formalmente

$T(n) = \Omega(g(n))$ se existem constantes positivas $c$ e $n_0$ tais que $c g(n)\leq T(n)$ para todo $n\geq n_0$;

A notação $\Omega$

• Graficamente:

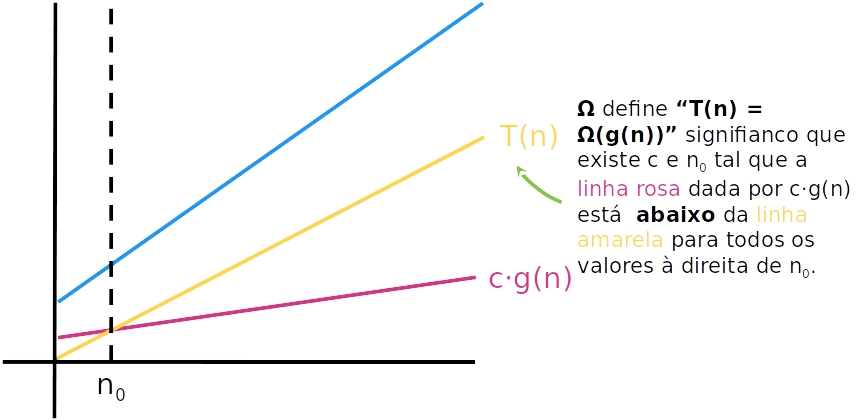
A notação $\Omega$

• Similarmente, podemos provar que $T(n) = \Omega(g(n))$, temos que mostrar que existe um $c$ e $n_0$ que satizfaz a definição.

• Por exemplo, queremos provar que $T(n) = 10n^2+ 5n+ 3$ and $g(n) = n^2$. Podemos mostrar que $T(n) = \Omega(g(n))$ encontrando um $c$ e $n_0$ de acordo com a definição. Por exemplo:

  $c \leq 10 + \frac{5}{n} + \frac{3}{n^2}$

para $n\geq 1$ temos que

$10 + \frac{5}{n} + \frac{3}{n^2} \geq 10$

Basta tomar $n_0=1$ e $c=10$, que $T(n) = \Omega(g(n))$

A notação $\Theta$

• Dizemos que $T(n) = \Theta(g(n))$ se, e somente se:

  • $T(n) = O(g(n))$ e
  • $T(n) = \Omega(g(n))$

• $T(n) = 10n^2+ 5n+ 3 = \Theta (n^2)$ pois, como vimos anteriormente, $T(n) = 10n^2+ 5n+ 3 = O (n^2)$ e $T(n) = 10n^2+ 5n+ 3 = \Omega (n^2)$

Propriedades da notação assintótica

• Sejam $f(n)$, $g(n)$ e $h(n)$ funcoes positivas. Temos que:

1. $f(n) = \Theta(f(n))$;
2. $f(n) = \Theta(g(n))$ se e somente se $g(n) = \Theta(f(n))$;
3. $f(n) = O(g(n))$ se e somente se $g(n) = \Omega(f(n))$;
4. Se $f(n)=O(g(n))$ e $g(n) = \Omega(h(n))$, então $f(n) =O(h(n))$; O mesmo vale substituindo $O$ por $\Omega$;
5. Se $f(n) = Θ(g(n))$ e $g(n) =O(h(n))$, entao $f(n) =O(h(n))$; O mesmo vale substituindo $O$ por $\Omega$;
6. $f(n) =O(g(n) +h(n))$ se e somente se $f(n) =O(g(n)) +O(h(n))$; O mesmo vale substituindo $O$ por $\Omega$ ou por $\Theta$;
7. Se $f(n) =O(g(n))$ e $g(n) =O(h(n))$, entao $f(n) =O(h(n))$; O mesmo vale substituindo $O$ por $\Omega$ ou por $\Theta$.

Complexidade do InsertionSort

• A complexidade do InstertionSort é:

Complexidade do InsertionSort

• Relembre que, no melhor caso
  $T(n) = 5n -3$

• De acordo com as propriedades 1 e 2, temos que:

$T(n) = 5n -3 = \Theta(n)$

Complexidade do InsertionSort

• Relembre que, no pior caso
  $T(n) = n^2 + 2n - 6$
• Podemos provar como fizemos anteriormente (encontrar $c$ e $n_0$), mas obserse que, para qualquer $T(n)$ na forma:
  $T(n) = an^2 + bn + c$
  se tomarmos $n_0=1$ e notar que para todo $n \geq n_0$ temos que
  $an^2\leq an^2 + bn + c\leq (a+b+c)n^2$
  escolhendo $c=a$ e $C=a+b+c$ na definição de $O$ e $\Omega$ (por consequencia $\Theta$), temos que
  $T(n) = n^2 + 2n - 6 = \Theta(n^2)$

Função assintótica de polinômios

• Com uma análise similiar, podemos mostrar que para qualquer polinômio
  $T(n) = \sum_{i=1}^k a^i n^i$
  em que $a_i$ é uma constante para $i \in 1..k$, e $a_k > 0$, temos que

$T(n) = \Theta(a^k)$

Complexidade do InsertionSort

• Relembre que, no caso médio
  $T(n) = 2n + \frac{n(n-1)}{4} = \frac{n^2}{4} + \frac{7n}{4}$
  que é similar ao caso anterior, portanto
  $T(n) = 2n + \frac{n(n-1)}{4} = \Theta(n^2)$

Complexidade do InsertionSort

• Na prática, como estamos interessados no comportamento assintótico, não precisamos fazer uma análise tão cuidadosa como a que fizemos no início da aula.
  • Por exemplo, não precisamos contar as linas 2,3,7 e 5,6, pois "o que importa" é número de repetições do laço
• Essa é uma das vantagens de se utilizar notação assintótica para estimar os recursos de um algoritmo

Complexidade

• Em geral, quando falamos da complexidade de um algoritmo, estamos interessados no pior caso
  • nem sempre é fácil definir um "caso médio"
• Qual é o limite superior do pior caso desse algoritmo?

Complexidade do InsertionSort

• É possível fazer melhor?
  • Sim, mas veremos nas próximas aulas 😃