Lidando com problemas intratáveis

• Suponha que você se depare com um problema $NP$-Difícil

• A teoria nos diz que é imporvável encontrar um algoritmo polinomial para o problema

• Devemos desistir?

  • Provavelmente sim, se o objetivo for realmente encontrar um algoritmo polinomial
  • Provavelmente não, se o seu trabalho depende disso

Lidando com problemas intratáveis

• Melhorando com relação a força bruta

  • Desenvolver estatégias que identificam e armazenam soluções já calculadas (programação dinâmica).
  • Garantia de encontrar a solução ótima,
  • Sem garantia de tempo polinomial

• Heurísticas

  • Desenvolver algoritmos intuitivos
  • Garantia de execução em tempo polinonimal
  • Sem garantia de qualidade da solução

Lidando com problemas intratáveis

• Algoritmos aproximados
  • Garantia de execução em tempo polinomial
  • Garantia de encontrar uma solução de alta qualidade (digamos, $95 \%$ do ótimo)
  • Problema: temos que mostrar que uma solução está próxima do ótimo, mesmo sem saber qual é o valor ótimo!

Mochila inteira

• Resolver o problema da mochila por força bruta tem complexidade $O(n2^n)$, pois existem $O(2^n)$ combinações e levamos um tempo $O(n)$ para verificar cada uma
• Quando estávamos estudando programação dinâmica, vimos um algoritmo para resolver o problema da mochila
• Essa abordagem tem complexidade $O(n2^{\log W})$, em que $W$ é o tamanho da mochila

Mochila inteira

• E se usarmos a estratégia gulosa da mochila fracionária para a mochila inteira?

  1. Ordenar e reindexar os itens tal que
     $\frac{v_1}{w_1}\geq\frac{v_1}{w_1}...\geq\frac{v_n}{w_n}$
  2. Passo:2 Selecionar os itens em ordem até que algum não caiba, e paramos

Mochila inteira

• Considere uma mochila com capacidade $W=5$, e a seguinte lista de itens:

• Nesse caso, o algoritmo guloso seleciona os itens $\{1,2\}$, que nesse exemplo é a mesma da solução ótima

Mochila inteira

• Considere uma mochila com capacidade $W=1000$, e a seguinte lista de itens:

• Nesse caso, o algoritmo guloso seleciona apenas o item $\{1\}$, que neste caso está muito distante da solução ótima!

Mochila inteira

• Uma heurística melhorada que a anterior é:
  1. Ordenar e reindexar os itens tal que
     $\frac{v_1}{w_1}\geq\frac{v_1}{w_1}...\geq\frac{v_n}{w_n}$
  2. Selecionar os itens em ordem até que algum não caiba, e paramos
  3. retornar o máximo entre o passo 2 ou o item de maior valor

Garantia de desempenho

• Teorema: o algoritmo guloso de 3 passos encontra uma solução que sempre é maior que 50% da solução ótima.
• Prova: no passo 2, suponha que o algoritmo seleciona os primeiros $k$ itens, ordenados pela razão valor/peso.
  • Seja $c(S)$ o valor da solução do algoritmo de 3 passos
  • Seja $c(S_k)$ o valor da solução de selecionar os primeiros $k$ itens
  • Seja $v_{k+1}$ o valor do item $k+1$

Garantia de desempenho

• Como no passo 3 pegamos o máximo entre os $k$ primeiros itens que cabem na mochile ou os itens remanescentes, temos que

  $c(S) \geq c(S_k) \tag 1$
  $c(S) \geq v_{k+1} \tag 2$

• Combinando (1) e (2), temos que

$2c(S) \geq c(S_{k+1}) \tag 3$

Garantia de desempenho

• O item $k+1$ não cabe na mochila, mas vamos assumir que podemos selecionar uma fração dele (como na mochila fracionária)
• Seja $c(S'_{k+1})$ o valor dessa mochila fracionária hipotética, e $S^*$ o valor da solução ótima
• Na mochila fracionária preenchemos a mochila completamente e de maneira ótima, então a solução gulosa da mochila fracionária deve ser maior ou igual ao da solução ótima inteira

Garantia de desempenho

• Resumindo:
  $2c(S) \geq c(S_{k+1}) \tag 3$
  $c(S'_{k+1}) \geq c(S^*) \tag 4$

• Combinando (3) e (4), temos que

$\begin{aligned} 2c(S) &\geq c(S^*)\\ c(S) & \geq \frac{c(S^*)}{2} \end{aligned}$

o que prova o teorema

Aproximação arbitrariamente boa

• Objetivo: para um parametro $\epsilon$ especificado pelo usuário, queremos garantir $(1-\epsilon)\%$ de aproximação

• Limitação: o tempo de execução aumenta a medida que $\epsilon$ diminui. (estamos trocando tempo computacional por garantia de qualidade)

Aproximação arbitrariamente boa

• Ideia em alto nível: resolver de maneira exata um problema aproximado, mas que é mais fácil de resolver

• Para o problema da mochila, podemos arredondar o valor dos itens para um inteiro pequeno.

• Existe uma varição do algoritmo que executa em $O(n^2 V_{\max})$, em que $V_{\max} = \max v_i$

Aproximação arbitrariamente boa

• Por exemplo considere uma mochila com capacidade $W=11$. O valor original na tabela da esquerda pode ser aproximado pelos valores da tabela da direita

Aproximação arbitrariamente boa

• Arredondar os valores, dividindo por um parâmetro $\theta$ :
  $\hat{v_i} = \left\lfloor \frac{v_i}{\theta}\right\rfloor$
• Em que o parâmetro $m$ é definido em função do parâmetro de qualidade $\epsilon$ especificado pelo usuário:
  $\theta = \frac{\epsilon \cdot V_{\max}}{n}$

Duas abordagnes para a mochila inteira

• Na primeira versão do algoritmo de programação dinâmica,

Qual é o valor máximo que conseguimos colocar no espaço W, considerando os primeiros $n-1$ itens.

• Uma maneira diferente de abordar o problema é

Qual é o espaço mínimo necessário para obter valor X com os primeiros primeiros $n-1$ itens

Duas abordagnes para a mochila inteira

• Na primeira versão do algoritmo de programação dinâmica, temos a relação de recorrência
  $V_{n, W}=\left\{\begin{array}{ll}{\max \left\{V_{n-1, W}, V_{n-1, W-w_{n}}+v_{n}\right\}} & {\text { se } w_{n} \leq W} \\ {V_{n-1, W}} & {\text { se } w_{n}>W}\end{array}\right.$
• Na segunda versão, temos:
  $V_{n, W}=\left\{\begin{array}{ll}{\min \left\{V_{n-1, X}, V_{n-1, X-v_{n}}+w_{n}\right\}} & {\text { se } v_{n} \leq X} \\ {V_{n-1, X}} & {\text { se } v_{n}>X}\end{array}\right.$

Comparando algoritmos

• Força Bruta: $O(n2^n)$
• Primeiro algoritmo de programação dinâmica $O(nW) = O(n2^{\log W})$
• Segundo algoritmo de programação dinâmica $O(nV) = O(n2^{\log V})$
• Casos especiais:
  • Podemos usar o primeiro algoritmo se a capacidade da mochila é pequena e fixada
  • Podemos usar o segundo algoritmo se o valor total é fixado

Aproximação arbitrariamente boa

• Para uma solução $S$, seja $c(S)$ o valor da solução no problema original, e $c'(S)$ o valor da solução do problema aproximado.

• Seja $S^*$ a solução ótima no problema original, e $S'^*$ a solução ótima no problema simplificado

• Queremos achar um limite para
  $c(S^*) - \theta c'(S'^*)$

• O valor da soluçõa ótimos é $c(S*)$, e nossa aproximação retorna $\theta c'(S'^*)$

Aproximação arbitrariamente boa

• Observe que
  $c'(S'^*) \geq c'(S^*)$
  • Raciocínio: $S'^*$ é a solução ótima para o problema reduzido, então o seu valor no problema reduzido é pelo menos o valor de qualquer solução de qualquer solução no problema reduzido, incluindo $S^*$
• Então
  $c(S^*) - \theta c'(S'^*) \leq c(S^*) - \theta c'(S^*)$

Aproximação arbitrariamente boa

• Agora observe que:
  $\begin{aligned} c\left(S^{*}\right)-\theta c^{\prime}\left(S^{*}\right) &=\sum_{i \in S^{*}} v_{i}-\theta \sum_{i \in S^{*}}\left\lfloor\frac{v_{i}}{\theta}\right\rfloor \\ &=\sum_{i \in S^{*}}\left(v_{i}-\theta\left\lfloor\frac{v_{i}}{\theta}\right\rfloor\right) \\ &<\sum_{i \in S^{*}} \theta \\ &=n \theta \end{aligned}$
  Então $c(S^*) - \theta c'(S^*) \leq n\theta$

Aproximação arbitrariamente boa

• Substituindo, temo que:
  $\begin{aligned} c(S^*) - \theta c'(S'^*) & \leq n\theta \\ c(S^*) - n\theta & \leq \theta c'(S'^*) \end{aligned}$
• Se $n\theta \leq \epsilon c(S^*)$, então $(1-\epsilon) c(S^*) \leq c'(S'^*)$, então temos que escolher $\theta \leq \frac{\epsilon c(S^*)}{n}$
• Um limite inferior para $c(S^*)$ é o item de maior valor $V_{max}$ que cabe na mochila. Então podemos escolher

$\theta \leq \frac{\epsilon V_{\max}}{n}$

Aproximação arbitrariamente boa

• Para qualquer $\theta$, o tempo de execução é $O(nV/\theta)$

• Já que $\theta = \frac{\epsilon V_{\max}}{n}$, o tempo de execução é $O\left(n^2\frac{V}{\epsilon V_{\max}}\right)$

• Observe que $V\leq nV_{\max}$, então o tempo de execução é $O\left(\frac{n^3}{\epsilon}\right)$

• Um esquema de aproximação completamente em tempo polinomal (FPTAS - do inglês Fully Polinomial-Time Approximation Scheme) é um esquema de aproximação em que o tempo é polinomial no tamanho da entrada e $1/\epsilon$

FPTAS

• Alguns (mas não todos) algoritmos NP-difíceis podem ser aproximados usando FPTAS
• Mesmo que $P \neq NP$, ainda assim podemos aproximar a resposta para uma precisão arbitrária em tempo polinomial
• Se você optar por uma solução aproximada, em muitos casos você existem algoritmos eficientes

Problema do caixeiro viajante

• Um Ciclo Hamiltoniano em um grafo não dirigido $G$ é um ciclo simples que visita todos os nós de $G$

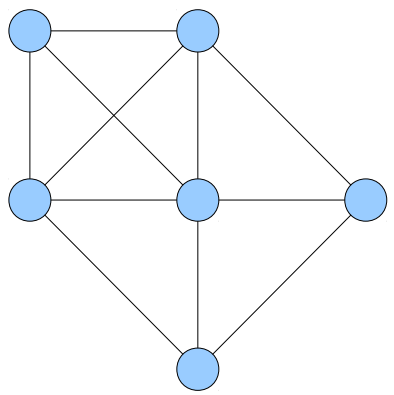
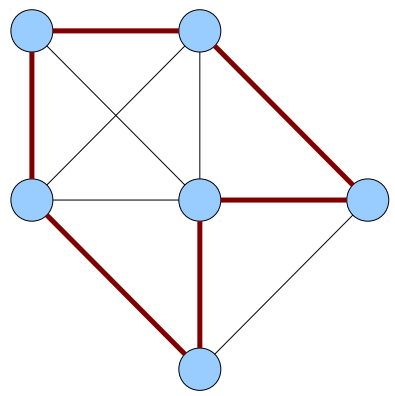
Problema do caixeiro viajante

• Dado um grafo $G$ completo e não dirigido, o problema do caixeiro viajante (TSP, do inglês Traveling Salesperson Problem) consiste em encontra o ciclo Hamiltoniano de custo mínimo

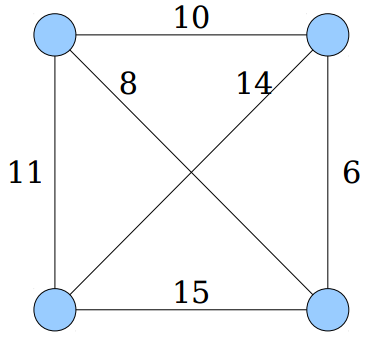
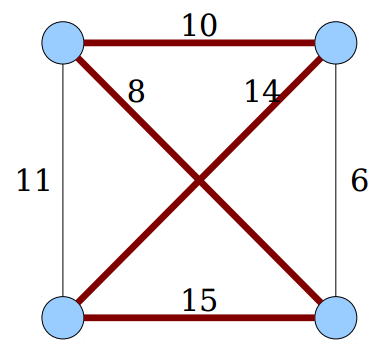
Custo 47

Problema do caixeiro viajante

• Dado um grafo $G$ completo e não dirigido, o problema do caixeiro viajante (TSP, do inglês Traveling Salesperson Problem) consiste em encontra o ciclo Hamiltoniano de custo mínimo

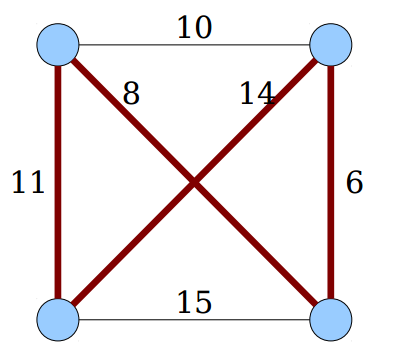
Custo 39

Problema do caixeiro viajante

• Dado um grafo $G$ completo e não dirigido, o problema do caixeiro viajante (TSP, do inglês Traveling Salesperson Problem) consiste em encontra o ciclo Hamiltoniano de custo mínimo

• Observe que se o grafo é completo, deve existir pelo menos um ciclo Hamiltoniano

• Esse problema é conhecido como sendo $NP$-Difícil

Problema do caixeiro viajante

• Uma solução por força bruta consiste em testar todos os ciclos Hamiltonianos
  • Quantos ciclos Hamiltonianos existem?
    Resposta: $(n-1)!/2$
  • Cosumimos $O(n)$ para processar cada ciclo
• Tempo total: $O(n!)$
• O que é completamente impraticável

Problema do caixeiro viajante

• Seja $C(v,S)$ o custo mínimo de um caminho $\{1, 2, \cdots, v\}$ que o último vértice é $v$, e passa por todos os vértices de $G$
• Seja $u$ o penúltimo vértice desse caminho, e $w(u,v)$ o custo da aresta $(u,v)$. Devemos usar $(u,v)$ se o caminho $\{1, 2, \cdots, u\}$ é ótimo, mais o custo $w(u,v)$, levando a seguinte equação de recorrência:

$C{v, S}=\left\{\begin{array}{ll}{\min_{u\in S\setminus v} \left\{C(u,S\setminus v)+w(u,v)\right\}} & {\text { se } w_{n} \leq W} \\ 0 & {\text { se } v=s \text{ e } S=\{s\}}\end{array}\right.$

Problema do caixeiro viajante

• Podemos usar programação dinâmica para armazear os subconjuntos de vértices já calculadas

• A ideia consiste em avaliar a equção de recorrência em conjuntos de tamanho crescente $(1,2,\cdots,n)$

• Existe $O(2^n)$ possíveis permutações de $S$.

• Podemos mapear cada subconjunto em um número inteiro usando uma máscara binária. Isso leva a um custo adicional de $O(n)$ para calcular a máscara que não contenha $v$.

Problema do caixeiro viajante

• Em resumo, temos $O(n2^n)$ subproblemas
• Resolver um subproblema de tamanho $n$ requer que analisemos $O(n)$ subproblemas, com um custo adicinal de $O(1)$ para cada
• O custo da abordagem de programação dinâmica é $O(n^22^n)$

Problema do caixeiro viajante

• Ainda é exponencial, mas compare o tempo para diferente entradas:

• Melhorar com relação à força bruta aumenta o tamanho dos problemas que conseguimos resolver em um tempo razoável

Problema do caixeiro viajante

• Provavelmente não é possível encontrar uma aproximação para o TSP com garantia $\epsilon$ e tempo polinomial
• Se relaxarmos o problema para desconsiderar os pesos, reduziriamos o problema a encontra um ciclo Hamiltoniano qualquer, que também não tem uma solução polinomial

Heurísticas

• Uma heurística para resolver o TSP consiste em encontrar a árvore geradora mínima (TSP)

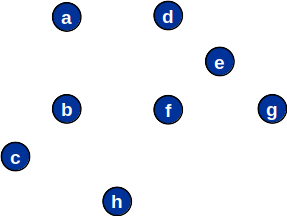
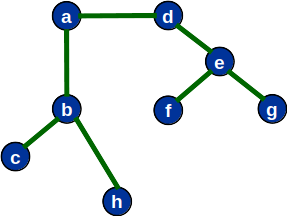
Heurísticas

• Uma heurística para resolver o TSP consiste em encontrar a árvore geradora mínima (TSP)
• Retornar o ciclo no pecurso em ordem da árvore

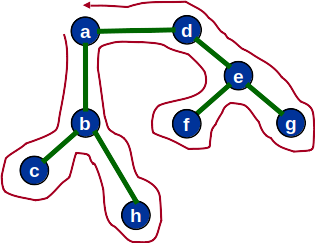
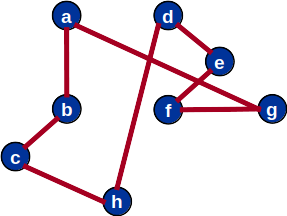
Heurísticas

• Uma heurística para resolver o TSP consiste em encontrar a árvore geradora mínima (TSP)
• Retornar o ciclo no pecurso em ordem da árvore

Ciclo Hamiltoniano a partir da MST

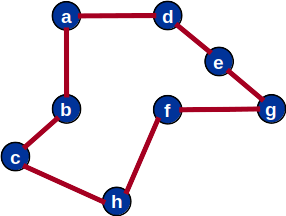
Solução ótima para o TSP

Heurísticas

• Assumindo que a distância entre os nós respeita a distância euclideana, podemos encontrar um PTAS para o TSP euclideado:
  • Uma aproximação cuja distância é no máximo duas vezes a do caminho ótimo pode ser encontrara em tempo polinomial usando o algoritmo de dobrar a árvore
  • No máximo 1,5 vezes a do caminho ótimo pode ser encontrada utilizando o algoritmo de Christofides

Lidando com problemas intratáveis

• Em resumo
  • Se precisa de uma solução exata, em geral podemos fazer melhor que força bruta (mas ainda em tempo não polinomial)
  • Se uma aproximação é suficiente, algumas vezes podemos encontrar algoritmos eficientes com garantia de proximidade.