Análise de Algoritmos
Ronaldo Cristiano Prati
Bloco A, sala 513-2
ronaldo.prati@ufabc.edu.br
Análise assintótica
(recapitulando)
-
Ao ver expressões como n+10 ou n2+1 pensamos geralmente em valores pequenos de n
-
A análise algoritmica faz justamente o contrário: ignora valores pequenos e concentra-se nos valores enormes de n
-
Esse tipo de análise se chama análise assintótica.
Notação assintótica
(recapitulando)
-
Ferramenta para analisar algoritmos e descrever a ordem de crescimento dos tempos de execução
-
Provê formalismo e vocabulário matemático que nos permitem argumentar sobre a qualidade e eficiência de algoritmos.
Notação assintótica O,Ω,Θ
(recordando)
-
T(n)=O(g(n)) se existem constantes positivas C e n0 tais que T(n)≤Cg(n) para todo n≥n0;
-
T(n)=Ω(g(n)) se existem constantes positivas c e n0 tais que cg(n)≤T(n) para todo n≥n0
-
Dizemos que T(n)=Θ(g(n)) se, e somente se:
- T(n)=O(g(n)) e
- T(n)=Ω(g(n))
Notação assintótica
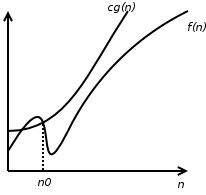
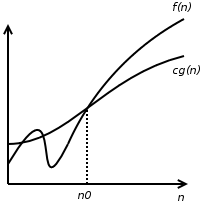
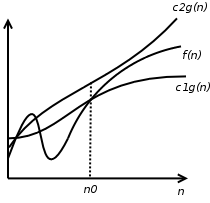
Notação assintótica
(recapitulando)
- Para valores enormes de n, as funções:
n2, 23n2 , 9999n2 , 1000n2, n2+100n ,
crescem todas com velocidades muito parecidas e portanto são todas "equivalentes" - Esse tipo de análise, interessado somente em valores enormes de n, é chamado assintótica. Nessa análise, as funções são classificadas em "ordens"; todas as funções de uma mesma ordem são "equivalentes"
- As cinco funções acima, por exemplo, pertencem à mesma ordem de crescimento
Notação assintótica o,ω
-
T(n)=o(g(n)) se existem constantes positivas c e n0 tais que 0≤T(n)<cg(n) para todo n≥n0;
-
T(n)=ω(g(n)) se existem constantes positivas C e n0 tais que T(n)>Cg(n) para todo n≥n0
Notação assintótica o,ω
- Por exemplo, 2n=o(n2), mas 2n2 não é o(n2)
- Se T(n)=o(g(n)), então T(n) é insignificante com relação a g(n), para n grande. Alternativamente, T(n)=o(g(n)) quando
n→∞limg(n)T(n)=0
- Por exemplo, 2n2=ω(n), mas 2n2 não é ω(n2)
- Se T(n)=ω(g(n)), então g(n) é insignificante com relação a T(n), para n grande. Alternativamente, T(n)=ω(g(n)) quando
n→∞limg(n)T(n)=∞
Notação assintótica
(Exemplo 1)
-
Mostre que T(n)=∑i=0kaini em que ai são constante para i∈0..k é O(nk)
-
Escolha n0=1 e c=∑i=0k∣ai∣. Temos que mostrar que ∀n≥1,T(n)≤cnk
T(n)≤∣ak∣nk+⋯+∣a1∣n+∣a0∣≤∣ak∣nk+⋯+∣a1∣nk+∣a0∣nk=cnk
Notação assintótica
(Exemplo 2)
-
Mostre que para todo k>1,T(n)=nk não é O(nk−1)
-
Por contradição, suponha que nk=O(nk−1). Então, ∃c,n0>0 tal que
nk≤cnk−1,∀n≥n0 -
Cancelando nk−1 de ambos os lados:
n≤c,∀n≥n0 -
O que é claramente falso (contradição).
Notação assintótica
(Exemplo 3)
-
Mostre que T(n)=2n+10 é O(2n)
-
Temos que escolher constantes n, n0 tal que
2n+10≤c2n,∀n>n0
- Observe que:
2n+10=210⋅2n=1024⋅2n
- Basta escolhermos c=1024 e n0=1
Notação assintótica
(Exemplo 4)
- Mostre que T(n)=210n não é O(2n)
- Por contradição. Se 210neˊO(2n), então ∃c,n0>0 tal que
-Temos que escolher constantes n, n0 tal que
210n≤c2n,∀n>n0 - Entretanto, cancelando 2n de ambos os lados
29n≤c,∀n>n0 - Que é obviamente falso
Notação assintótica
(Exemplo 5)
- Para cada par de funções positivas f(n) e g(n), mostrar que
max[f(n),g(n)]=Θ(f(n)+g(n)) - Para todo n temos que:
max[f(n),g(n)]≤f(n)+g(n) - e
2max[f(n),g(n)]max[f(n),g(n)]≥f(n)+g(n)≥21(f(n)+g(n)) - Então
21(f(n)+g(n))≤max[f(n),g(n)]≤f(n)+g(n),∀n≥1 - Portanto max[f(n),g(n)]=Θ(f(n)+g(n)), bastando escolher c=21 e C=1, para n0=1
Notação assintótica
(Exemplo 6)
-
Seja T(n)=10n+3logn, mostre que T(n)=o(n2)
-
Precisamos mostrar que 10n+3logn<cn2,∀n>n0.
-
Observe que 10n+3logn<13n
10n+3logn13n<cn2<cn2 -
Quando n>c13,∀c,13n<cn2, portanto T(n)=o(n2) com n0=13/c+1
Notação assintótica
Algumas classes de ordem mais comuns são:
| Função g(n) | Classe |
|---|---|
| 1 | Constante |
| logn | Logarítmica |
| n | Linear |
| nlogn | Loglinear |
| n2 | Quadrática |
| n3 | Cúbica |
| 2n | Exponencial |
| n! | Fatorial |
Classes de problemas mais comuns
- Constante T(n)=O(1) - número fixo de operações
- Logarítmica T(n)=O(logn) - ocorre tipicamente em algoritmos que dividem um problema grande em dois menores, e assim sucessivamente. Se n é mil, log2n≈10, se n é um milhão, log2n≈20 (a base do algoritmo importa pouco).
- linear T(n)=O(n) - algumas operações (fixas) são executadas para cada elemento. Cada vez que n dobra de tamanho, o tempo de execução também dobra
Classes de problemas mais comuns
- log-linear T(n)=O(nlogn) - ocorre tipicamente quando um problema é quebrado em problemas menores, sendo que cada um deles é resolvido independentemente e depois juntando soluções. Quando n é um milhão, nlog2n é 20 milhões. Para n 2 milhões, nlog2n é 42 milhões
- quadrático T(n)=O(n2) - caso típico é um laço dentro do outro. Se n é mil, o número de operações é 1 milhão. Quando n dobra, o número de operações é multiplicado por 4
- cúbico T(n)=O(n3) - caso típico são três laços aninhados. Se n é cem, o número de operações é 1 milhão. Quando n dobra, o número de operações é multiplicado por 8
Classes de problemas mais comuns
- exponencial T(n)=O(2n) - usa força bruta para resolver um problema, e não tem aplicações práticas para n grande. Se n=20, são necessárias na ordem de 1 milhão de operações. Quando n dobra, o tempo de execução é elevado ao quadrado
- fatorial T(n)=O(n!) força bruta, mas muito pior que O(2n). Se n = 20, 20! = 2432902008176640000, se n = 40, 40! = 815915283247897734345611269596115894272000000000, se n = 60, 60! = 832098711274139014427634118322336438075417 2606361245952449277696409600000000000000
Classes de complexidade
| Função | Computador Atual | Computador 100x mais rápido | Computador 1000x mais rápido |
|---|---|---|---|
| log10n | N1 | 103N1 | 104N1 |
| n | N2 | 100N2 | 1000N2 |
| nlog10n | N3 | 50N3 | 333N3 |
| n2 | N4 | 10N4 | 31.6N4 |
| n3 | N5 | 4.6N5 | 10N5 |
| 2n | N6 | N6+6 | N6+10 |
Classes de Complexidade
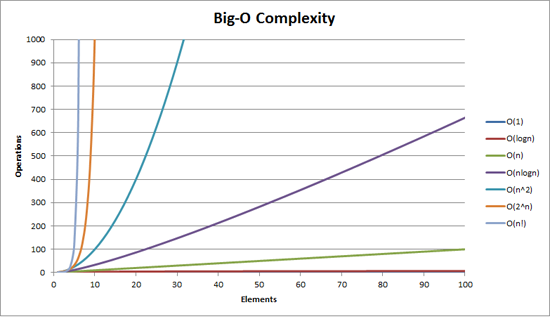
Complexidade do problema versus complexidade do algoritmos
- Em análise de algoritmos, podemos fazer a análise de duas maneiras distintss:
- Análise de um algoritmo em particular: Quantos recursos (tempo, memória) o algoritmo X precisa para rodar, em função do tamanho dos dados de entrada
- Análise de um problema: Em que procuramos pelo limite inferior de recursos para resolver um determinado problema
Complexidade do problema versus complexidade do algoritmos
- Em alguns casos, as duas coisas estão ligadas: mesmo sem um resultado teórico, existe o algoritmo A para um problema, que consome x recursos, e A é o melhor algoritmo conhecido para aquele problema. Ou seja, não existe (ou é muito difícil) uma análise teórica, mas conhecemos um algorithmo que resolva com recursos x)
- Também existem casos em que existe um limite inferior, mesmo que não se conheça um algoritmo com o desempenho daquele limite inferior (multiplicação de matrizes é um exemplo). Nesse caso, existe um resultado teórico para o problema, mas um algoritmo que consumo no máximo aquele limite teórico não é conhecido
Limite superior
-
A notação O também é utilizada para indicar limites superiores para problemas
-
Por exemplo, dado o problema de multiplicação de duas matrizes n×n
- Conhecemos um algoritmo para resolver esse problema (pelo método trivial) de complexidade O(n3)
Cota superior
- A cota superior é a complexidade do melhor algoritmo conhecido para aquele problema
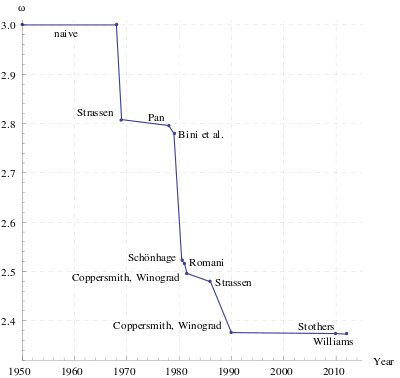
Analogia com record mundial
-
A cota superior para um problema é análogo ao recorde mundial para uma modalidade do atletismo
-
Ele é estabelecido pelo melhor atleta (algoritmo) do momento
-
Assim como o record mundial, a cota superior pode ser melhorada por algoritmo (atleta) mais veloz.
Limite inferior
- Às vezes é possível demonstrar que, para um problema, qualquer que seja o algoritmo, o problema requer pelo menos um certo número de operações.
- Para o problema de multiplicação de matrizes, apenas ler os elementos leva tempo O(n2)
- Assim, uma cota inferior trivial é Ω(n2)
Algoritmo Ótimo
- Se um algoritmo tem uma complexidade igual à cota inferior do problema, ele é assintoticamente ótimo (ou simplesmente ótimo)