Complexidade do InsertionSort

(recapitulando)

• A complexidade do InstertionSort é:

  Melhor caso	Caso médio	Pior caso
  $\Theta(n)$	$\Theta(n^2)$	$\Theta(n^2)$

• O InsertionSorte é um algoritmo que ordena qualquer vetor de $n$ elements em $O(n)$.

  • Não podemos dizer que InsertionSorte é $\Theta(n^2)$ pois no melhor caso o algoritmo executa em $\Theta(n)$.

• Podemos fazer melhor?

Divisão e Conquista

• Nós vamos usar um princípio parecido com o utilizado no algoritmo de Karatsuba de multiplicação de inteiros:
  • Recursivamente dividir um problema grande em problemas menores (divisão)
  • Resolver o problema menor (caso base)
  • Combinar as soluções parciais para resolver o problema maior (conquista)

Merge Sort

• A ideia do Merge Sort é dividor o problema em problemas menores, que podem ser mais facilmente resolvidos

  • divida os elementos em $2$ sub-vetores de tamanho (aproximadamente) $n/2$;
  • ordene cada sub-vetor (recursivamente)
  • intercale pares de sub-vetores adjacentes, em ordem

• A ordenação de cada sub-vetor é feita por meio de uma chamada recursiva em cada sub-vetor, até que cada sub-vetor tenha apenas um elemento (naturalmente ordenado)

Merge Sort

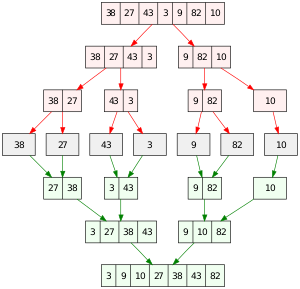
Merge Sort

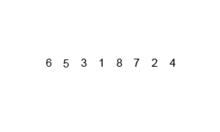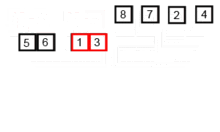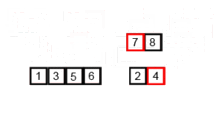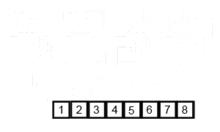
Merge Sort

• No método recursivo, passamos os limites (início, fim), do pedaço do vetor que estamos ordenando

• Se esses limites forem iguais, não precisa fazer nada (só tem um elemento, então é naturalmente ordenado)

• Caso contrário, "dividimos" o vetor em 2, e fazemos uma chamada recursiva para ordenar cada metade.

• Após o final dessas chamadas, fazemos a combinação usando a função Combina

Merge Sort

• A função recursiva MegerSort

(retirado daqui)

Combinação (Merge)

• Temos dois vetores ordenados, cada uma com o menor valor na primeira posição. Aquela que tiver o menor valor será o primeiro elemento no vetor intercalado.

• Uma vez que o menor valor é removido, examine novamente o primeiro elemento de cada vetor. Aquele que for menor será o próximo item no vetor intercalado.

• Continue esse processo de pegar o menor elemento do início de cada vetor até que você chegue ao fim de um vetor. Os remanecentes do outro vetor podem ser diretamente copiados para o vetor final

Função Combina

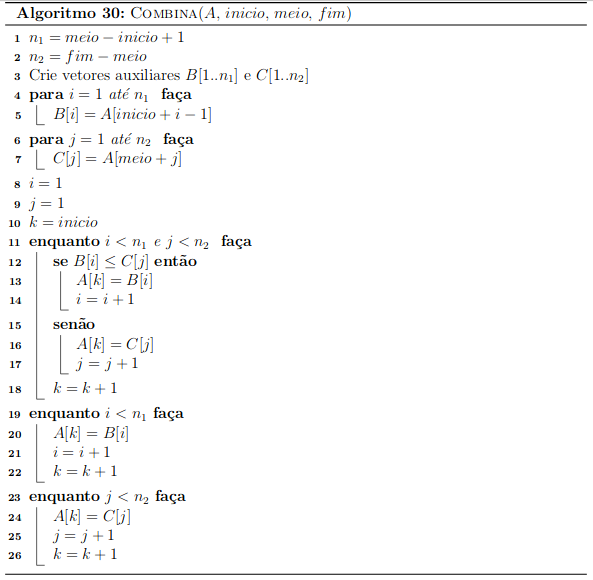
(retirado daqui)

Análise do MergeSort

• Vamos reponder as três perguntas com relação a análise de algoritmos:
  1. O algoritmo está correto?
  2. Quantos recursos o algoritmo consome?
  3. É possível fazer melhor?

O Algoritmo está correto?

• Hipótese de indução: "Em cada passo da chamada recursiva em um vetor de tamanho no máximo $i$, MergeSort retorna um vetor ordenado"

• Caso Base ($i=1$): um vetor de 1 elemento está sempre ordenado

• Passo de indução: Precisa provar que o método Combina mantém o vetor ordenado após a sua execução

• Conclusão: Ao final da execução, Combina junta todos os sub-vetores em um vetor ordenado.

(exercício): estude a prova por indução de na Seção 2.3.1 do livro do Cormen!

Complexidade do MergeSort

• Observe que o MergeSort requer memória extra na mesma proporção que o vetor original ($\Theta(n)$)

• Qual é a complexidade de tempo de MergeSort?

  • No caso base, o algoritmo executa uma tarefa que é $\Theta(1)$
  • Caso contrário, o tempo gasto será o tempo de ordenar cada uma das metades, mais o tempo de fazer a combinação

Complexidade do MergeSort

• Seja $n = fim - inicio$

• Na etapa de combinação, temos que combinar dois (sub) vetores de tamanho $n_1 = \lceil \frac{n}{2} \rceil$ e $n_2 = \lfloor \frac{n}{2} \rfloor$

• É fácil verificar que Combina consome $\Theta(n)$ operações:

  • Os laços das linhas 4 e 6 executam $T(n) = n_1 + n_2 = \Theta(n)$
  • De manira similar, os laços das linhas 11, 19 e 23 também são executados $T(n) = n_1 + n_2 = \Theta(n)$ (é fácil ver isso observado os valores que $k$ assume)

Equação de recorrência

• Podemos escrever a equação do tempo $T(n)$ gasto pelo MergeSort utilizando uma Equação a recorrência:

$T(n) = \begin{cases} \Theta(1), & \text{se }n\text{ = 1} \\ 2T(n/2) + \Theta(n), & \text{se }n > \text{ 1} \end{cases}$

Equação de recorrência

''Desenrolando" a quação de recorrência

• Para facilitar as contas, vamos assumir que $n$ é uma potência de 2, ou seja $n = 2^k$ (como estamos considerando análise assintótica, podemos imaginar que estamos arredondanto para cima caso não seja)

$\begin{aligned} T(2^k) & = 2 T(2^{k-1}) + 2^k \\ & = 2^2 T(2^{k-2}) + 2^1 2^{k-1} + 2^k\\ & = 2^3 T(2^{k-3}) + 2^2 2^{k-2} + 2^1 2^{k-1} + 2^k \\ & = 2^k T(1) + 2^{k-1}2^1 + ... + 2^1 2^{k-1} + 2^k \\ & = 2^k + 2^{k-1}2^1 + ... + 2^1 2^{k-1} + 2^k \\ & = (k+1) 2^k\\ & = k2^k + 2^k \end{aligned}$

"Desenrolando" a quação de recorrência

• Como $2^k = n$, podemos reescrever
  $\begin{aligned} T(n) & = n \log n + n \\ T(n) & = \Theta(n \log n) \end{aligned}$

• Portanto, a complexidade do MergeSort é $\Theta(n \log n)$

Podemos fazer melhor?

• Existe um algoritmo de ordenação de vetores com complexidade menor que $\Theta(n \log n)$?
• Existe um limite inferior de complexidade de métodos de ordenação?

Limite inferior

Teorema: O limite inferior de complexidade para algoritmos baseados em comparação direta dos elementos é $\Omega (n \log n)$

Limite inferior

• Para uma vetor $A$ de $n$ elementos, existem $n!$ possíveis permutações de posições entre eles

• Um algoritmo que considera todas as possíveis permutações teria uma complexidade $O(n!)$

Árvore de decisão

• Podemos usar comparações entre elementos para organizar essa permutações, de maneira a não considerar todas elas na ordenação.

• Essa organização forma uma árvore de decisão:

  • Cada nó da árvore contém uma comparação entre dois elementos. De um lado, colocamos as permutações em que a comparação é verdadeira, e de outra as permutações são falsas

  • Nas folhas, deve haver apenas permutações únicas

Árvore de decisão

• Para o caso de $n = 3$, e $A = [1,2,3]$, teríamos por exemplo:

Árvore de decisão

• Uma árvore como essa pode ser usada por um algoritmo de ordenação para encontrar a permutação ordenada sem considerar todas as possíveis permutações.

• O algoritmo percorre um ramo da árvore da raíz até uma folha, fazendo as comparações indicadas nos nós.

• O número máximo de comparações (pior caso) é equivalente a altura máxima da árvore.

Limite inferior

• Seja $m$ o número de permutações em um determinado nó da árvore. O algoritmo ideal de ordenação divide o número de permutações em duas partes de tamanho $\lceil \frac{m}{2} \rceil$ e $\lfloor \frac{m}{2} \rfloor$

  • Como uma comparação pode quebrar o problema em dois menores, idealmente queremos dividir o problema grande em dois menores de tamanho equivalente

• Qual é a altura máxima da árvore de um algoritmo de ordenação ideal?

Limite inferior

• Para facilitar a análise, vamos considerar que o $n$ é uma potência de 2 (caso não seja, podemos considerar o primeiro inteiro potência de 2 que é maior que $n$)

• Seja $h$ a altura da árvore do algoritmo ideal. Nesse caso, o número máximo de comparações é $2^h$. Temos que:

$\begin{aligned} 2^h & \geq n! \\ h & \geq \log n! \\ h & \geq n \log n \\ h & = \Omega(n \log n) \end{aligned}$

Limite inferior

• Em outras palavras, o número mínimo que comparações que um algoritmo de ordenação deve realizar para ordenar qualquer vetor de $n$ elementos é $\Omega(n \log n)$

• O MegerSort realiza $\Theta(n \log n)$ comparações, portanto o MergerSort pode ser considerado um algortimo cuja complexidade assintótica é ótima!

Ordenação linear

• Apesar desse limite $\Omega(n \log n)$ para algoritmos baseados em comparações, existem algoritmos com uma ordem de complexidade mais baixa, mas precisamos fazer suposições adicionais sobre os itens a serem ordenados

• Um exemplo é o Radix Sort

Radix Sort

• Radix Sort ordena cada "posição" do elemneto individualmente.

• Refaz o processo para cada dígito

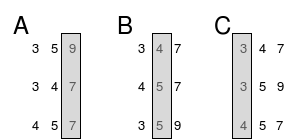
Radix Sort

• Podemos usar o fato de que o número de valores que cada dígito pode assumir é fixo para realizar cada passagem de maneira eficiente.

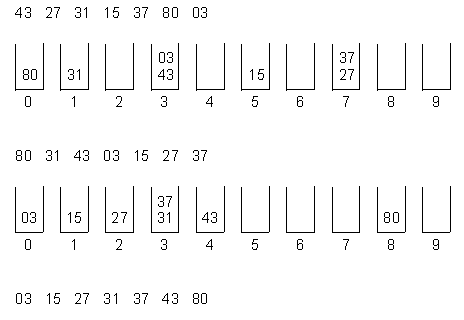
Radix Sort

• Por exemplo, considere que queremos ordenar o Código de Endereçamento Postal (CEP), que no brasil tem os 8 dígitos, começando do menos significativo, depois o segundo, e assim por diante, até oredenar os 8 dígitos

• Como sabemos quantos valores cada posição pode assumir (0 a 9), na ordenação de um dígito podemos simplesmente ir agrupando os elementos de acordo com o seu valor (que consome tempo linear).

• Como o número de dígitos do CEP é fixo (uma constante), e cada um consome tempo linear, nessa aplicação o RadixSort consome tempo linear.

Limite inferior

• A análise anterior não contradiz o fato que existe uma cota inferior para o número de comparações para a ordenação de quaisquer vetores

• Usamos o fato que, para um problema em particular, é possível usar a informação que os elementos tem um certo número de dígitos (8 no caso do CEP) para conseguir uma estratégia mais eficiente

• Outros algoritmos cujo tempo de ordenação é linear no número de elementos também fazem suposições sobre os elementos a serem ordenados.