Análise de Algoritmos
Ronaldo Cristiano Prati
Bloco A, sala 513-2
ronaldo.prati@ufabc.edu.br
Resolução de exercícios
- Dado que f(n)=logn e g(n)=log(100n), mostre que f(n)=O(g(n))
lognlogn1/221×log(100n)logn21×log(100)+log(n)logn≤clog(100n)≤clog(100n)≤c≤c
- Observe que para n≥1, o termo log(100)+log(n)logn está constrito entre 0 e 1, portanto, podemos escolher c>1/2 para um n0≥1
Resolução de exercícios
-
Dado que f(n)=n! e g(n)=nlogn, mostre que f(n) não é O(g(n))
-
Vamos provar por absurdo.
n!n(n−1)(n−2)!n(n−1)(n−2)!(n−2)!≤cnlogn≤cnlogn≤cn(n−1)≤c
- O quer claramente não é possível para n0>2, uma vez que n! (e por consequência (n−2)!) é sempre crescente, e não pode ser limita por uma constante.
Resolução de exercícios
- Ordene as funções a seguir em ordem crescente de taxa de crescimento:
T1T2T3T4=2n=n3/2=nlogn=nlogn
Resolução de exercícios
-
Afirmação 1: T3 é (assintoticamente) a menor delas, pois nenhuma delas é O(T3)
-
T2 não é O(T3). Vamos assumir que é, então
n3/2nlognn3/2lognn≤cnlogn≤c≤c -
n é maior que logn para n grande (limn→∞lognnp=∞,∀p>0 ), portanto não é possível ser limitada por uma constante
Resolução de exercícios
-
Afirmação 1: T3 é (assintoticamente) a menor delas, pois nenhuma delas é O(T3)
-
T4 não é O(T3). Vamos assumir que é, então
nlognnlognnlognlognnlogn−1≤cnlogn≤c≤c -
nlogn−1 é maior que logn para n grande, portanto não é possível ser limitada por uma constante
Resolução de exercícios
-
Afirmação 1: T3 é (assintoticamente) a menor delas, pois nenhuma delas é O(T3)
-
T1 não é O(T3). Vamos assumir que é, então
2nnlogn2n≤cnlogn≤c -
2n é maior que nlogn para n grande, portanto não é possível ser limitada por uma constante
Resolução de exercícios
-
Afirmação 2: A segunda (assintoticamente) menor é T2, pois T4 e T1 não são O(T2)
-
T4 não é O(T2). Vamos assumir que é, então
nlognn3/2nlognnlogn−3/2≤cn3/2≤c≤c -
que não é possível ser limitada por uma constante
Resolução de exercícios
-
Afirmação 2: A segunda (assintoticamente) menor é T2, pois T4 e T1 não são O(T2)
-
T1 não é O(T2). Vamos assumir que é, então
2nn3/22nn−23logn≤cn3/2≤c≤logc -
que não é possível ser limitada por uma constante
Resolução de exercícios
-
Afirmação3: T4 é (assintoticamente) menor que T1, pois T1 não é O(T4). Vamos assumir que é, então
2nnlogn2nn−lognlogn≤cnlogn≤c≤logc -
Observe que lognlogn é menor que nn=n, então n cresce mais rápido que lognlogn, e não é possível limitar por uma constante
Resolução de exercícios
- Juntanto as afirmações 1, 2 e 3 temos que (assintoticamente):
T3<T2<T4<T1
Árvore de recursão
- Árvore de recursão é um método muito útil para estimar a solução de uma recorrência
- Uma vez obtida a estimativa, podemos usar o método da substituição para prová-la
- A ideia consiste em representar o desenvolvimento da recorrência por meio de um diagrama (geralmente uma árvore), em que cada nó representa um subproblema, e somar os custos por nível
Árvore de recursão
- Considere por exemplo a relação de recorrência
T(n)=2T(n/2)+Θ(n)
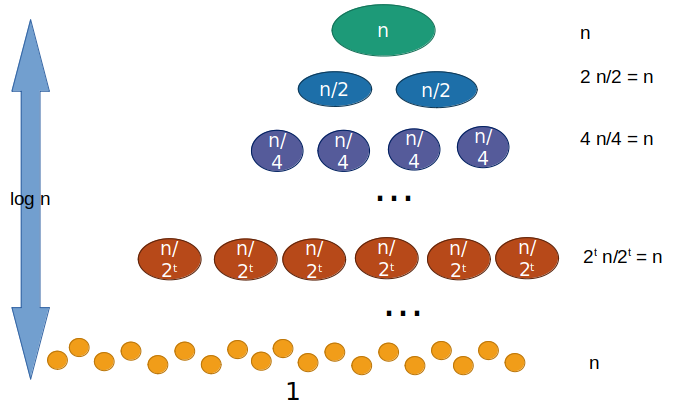
T(n)=t=0∑lognn=nlogn+n=Θ(nlogn)
Árvore de recursão
- Considere por exemplo a relação de recorrência
T(n)=T(n/2)+Θ(n)
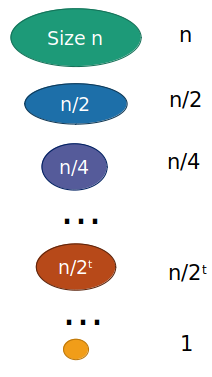
T(n)=t=0∑logn2tn=2n−1=Θ(n)
Árvore de recursão
- Considere por exemplo a relação de recorrência
T(n)=4T(n/2)+Θ(n)
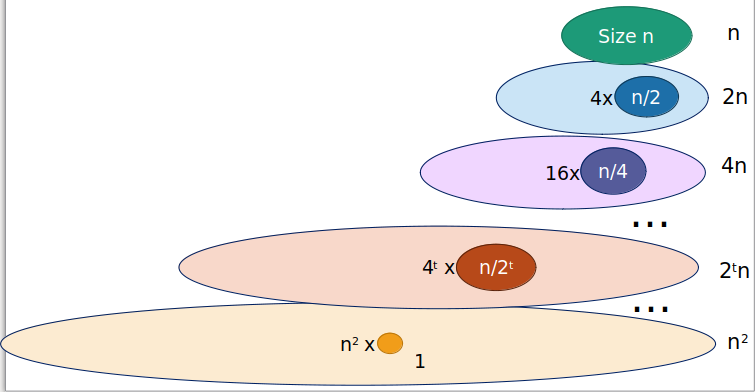
T(n)=t=0∑logn4t2tn=nt=0∑logn2t=n(2n−1)=Θ(n2)
Método Mestre (simplificado)
- O método mestre provê uma fórmula que pode ser aplicada a equações de recorrência do tipo:
T(n)=aT(bn)+Θ(nd) - em que:
- a é o número de suproblemas
- b fator em que o tamanho da entrada diminui
- d é necessário fazer nd trabalho adicional para criar os subproblemas e combinar as soluções
Método Mestre (simplificado)
- Seja:
T(n)=aT(bn)+Θ(nd) - Então
T(n)=⎩⎨⎧Θ(ndlog(n))Θ(nd)Θ(nlogb(a)) se a=bd se a<bd se a>bd
Método Mestre (simplificado)
T(n)=aT(bn)+Θ(nd)
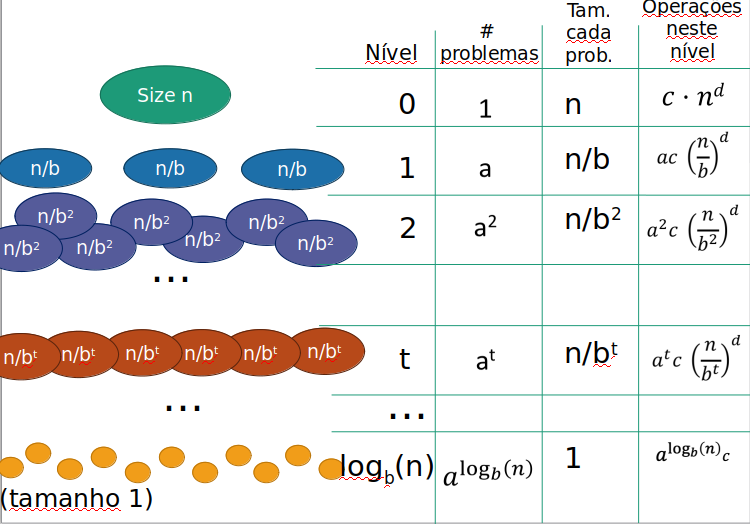
Método Mestre (simplificado)
- O número de computção no nível t é (no máixmo):
at⋅c⋅(btn)d=c⋅nd⋅(bda)t
- Em que:
- at: número de subproblemas no nível t
- (btn): tamanho de cada suproblema
- c(btn)d: a quatidade de trabalho para cada subproblema
Método Mestre (simplificado)
- Somando sobre todos os níveis temos que o total de trabalho é (no máximo):
T(n)=c⋅nd⋅t=0∑logbn(bda)t
Caso 1
- Nesse caso, a=bd
T(n)=c⋅nd⋅t=0∑logb(n)(bda)t=c⋅nd⋅t=0∑logb(n)1=c⋅nd⋅(logb(n)+1)=c⋅nd⋅(log(b)log(n)+1)=Θ(ndlog(n))
Caso 2
- Nesse caso, a<bd
- O termo bda é menor que 1, e ∑t=0logb(n)(bda)t converge para alguma constante menor que 1 :
i=0∑Nxt=x−1xN+1−1≤1−x1−xN+1≤1−x1=Θ(1)
Caso 2
- Nesse caso, a<bd
- O termo bda é menor que 1, e ∑t=0logb(n)(bda)t converge para alguma constante menor que 1:
T(n)=c⋅nd⋅t=0∑logb(n)(bda)t=c⋅nd⋅(alguma constate)=Θ(nd)
Caso 3
- Nesse caso, a>bd
- O termo bda é maior que 1:
i=0∑Nxt=x−1xN+1−1≤1−x1−xN+1≤xN(x−1x)=Θ(xN)
Caso 3
- Nesse caso, a>bd
- O termo bda é maior que 1:
T(n)=c⋅nd⋅t=0∑logb(n)(bda)t=Θ(nd(bda)logb(n))=Θ(nlogb(a))
Método mestre
- Em uma recorrência, temos dois fatores conflitantes:
- A divisão faz com que o número de problemas exploda!
- A maior parte do trabalho é feita na parte inferior da árvore
- Os problemas mais abaixo na árvore são menores
- A maior parte do trabalho está no topo da árvore
- A divisão faz com que o número de problemas exploda!
Método mestre
- Vamos considerar 3 exemplos para entender o método Mestre
- T1(n)=2T(n/2)+n
- T2(n)=T(n/2)+n
- T4(n)=4T(n/2)+n
Método mestre - Caso 1
-
A quatidade de trabalho é similar em cada nivel, e a complexidade é proporcional ao número de níveis vezes o trabalho por nível (caso 1)
T2(n)=2T(n/2)+n,a=bd=Θ(ndlogn)=Θ(nlogn)

Método mestre - Caso 2
- A maioria do trabalho é feita no topo (o maior problema), que é maior que o trabalho em qualquer nível e domina a recorrência (caso 2)
T2(n)=T(n/2)+n,a<bd=Θ(nd)=Θ(n)

Método mestre - Caso 3
- Há um grande número de folhas e o tempo é proporcional a processar as folhas (caso 3)
T2(n)=4T(n/2)+n,a>bd=Θ(nlog24)=Θ(n2)

Método Mestre (generalizado)
- O método mestre provê uma fórmula que pode ser aplicada a equações de recorrência do tipo:
T(n)=aT(bn)+f(n) - em que:
- a é o número de suproblemas
- b fator em que o tamanho da entrada diminui
- f(n) uma função
Método Mestre (caso geral)
- Seja:
T(n)=aT(bn)+f(n) - Então
T(n)=⎩⎨⎧Θ(nlogba)Θ(nlogbalogn)Θ(f(n)) se f(n)=O(nlogba−ϵ),ϵ>0 se f(n)=Θ(nlogba) se f(n)=Ω(nlogba+ϵ),ϵ>0 e af(n/b)≤cf(n),c<1
Método mestre
- O método mestre facilita a nossa vida
- Mas ele é basicamente uma mecanização dos cálculos que poderíamos fazer na mão se quisémos
- Nem sempre pode ser aplicado