Método mestre (simplificado)

(exemplo 1)

$T(n) = 9T\left(\frac{n}{3}\right) + n$

• $a=9, b=3, d=1, a > b^d (9 > 3^1)$
• Caso 3
• Pelo teorema mestre, $T(n) = \Theta(n^{\log_{3} 9} ) = \Theta(n^2)$

Método mestre (simplificado)

(exemplo 2)

$T(n) = T\left(\frac{2n}{3}\right) + 1$

• $a=1, b=3/2, d=0, a = b^d (1 = (3/2)^0)$
• Caso 1
• Pelo teorema mestre, $T(n) = \Theta(n^d\log (n) ) = \Theta(n^0\log n) = \Theta(\log n)$

Método mestre (simplificado)

(exemplo 3)

$T(n) = 2T\left(\frac{n}{2}\right) + c n^2$

• $a=2, b=2, d=2, a < b^d (2 > 2^2)$
• Caso 2
• Pelo teorema mestre, $T(n) = \Theta(n^d ) = \Theta(n^2)$

Método mestre (simplificado)

(exemplo 4)

$T(n) = 8T\left(\frac{n}{2}\right) + c n^2$

• $a=8, b=2, d=2, a > b^d (8 > 2^2)$
• Caso 3
• Pelo teorema mestre, $T(n) = \Theta(n^{\log_{2} 6} ) = \Theta(n^3)$

Método mestre (geral)

(exemplo 5)

$T(n) = 3T\left(\frac{n}{4}\right) + n \log n$

• $a=3, b=4, f(n) = n \log n$
• $n^{\log_b a} = n^{\log_4 3}$
• Além disso $f(n) = \Omega(n^{\log_4 3+\epsilon})$ e $a f\left(\frac{n}{b}\right) = 3\frac{n}{4}\log \left(\frac{n}{4}\right) \leq \left(\frac{3}{4}\right)n \log n$
• Caso 3
• Pelo teorema mestre, $T(n) = \Theta(n\log (n) )$

Método mestre (geral)

(exemplo 6)

$T(n) = 2T\left(\frac{n}{2}\right) + n \log n$

• $a=2, b=2, f(n) = n \log n$
• $n^{\log_b a} = n^{\log_2 2} = n$
• Caso 3?
• $f(n) \ne \Omega(n^{1+\epsilon})$, já que
  $\begin{aligned} n \log n & \ge n^{1 + \epsilon} \\ n \log n & \ge n\cdot n^{\epsilon} \\ \log n & \ge n^{\epsilon} \end{aligned}$
• Que como visto na aula passada é impossível (contradição). Nesse caso o teorema mestre não é aplicável e temos que resolver por meio de outro método

Quicksort

• Um dos algoritmos de ordenação mais usados na prática
• Não precisa de memória extra
• Pior caso $O(n^2)$, mas executa em $O(n \log n)$ no caso médio

Quicksort

• Ideia principal: particiona o vetor em torno de um elemento pivô.

• Usa um elemento do vetor como pivô

• Reorganiza o vetor de ta maneira que:

  • elementos à esquerda: menores que o pivô
  • elementos a direita: maiores que o pivô

• O pivô fica em sua posição correta

Quicksort

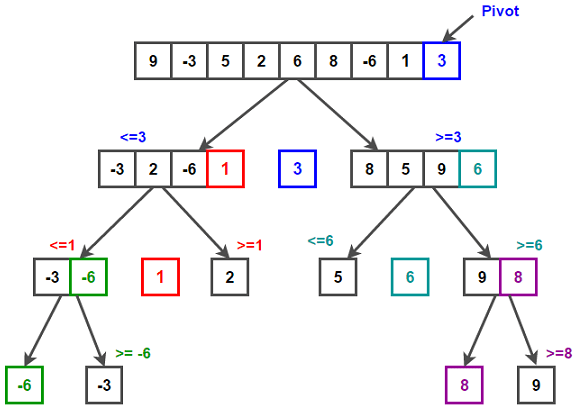
Quicksort

Propriedades Subrotina Particiona

• Cada etapa de partição pode ser executada em tempo linear $O(n)$
• Não precisa de memória extra
• Reduz o tamanho de problema

Subrotina Particiona

• Assuma que o pivô é o último elemento do (sub)vetor
  • Se não for, troque o pivô com o último elmento
• Ideia (alto nível):
  • Faz uma passada pelo vetor
  • invariante: os elementos vistos até o momento já estão particionados

Subrotina Particiona

• Usa duas variáveis auxiliares
  • $j$: elementos vistos até o momento
  • $i$: elementos em $A[inicio..j]$ que são menores que o pivô

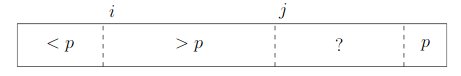
Subrotina Particiona

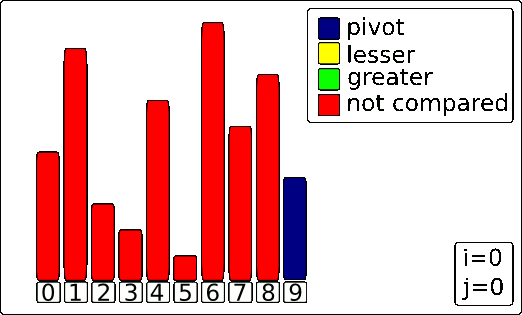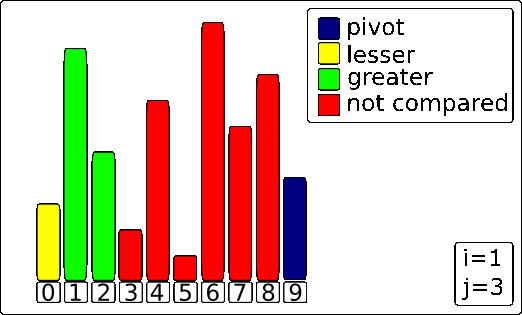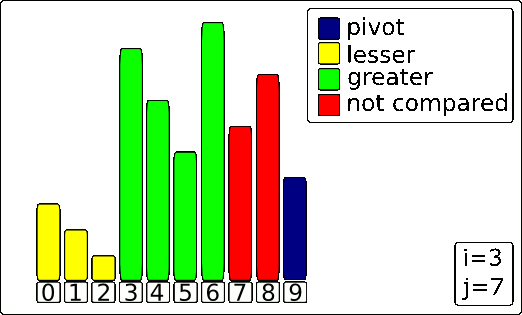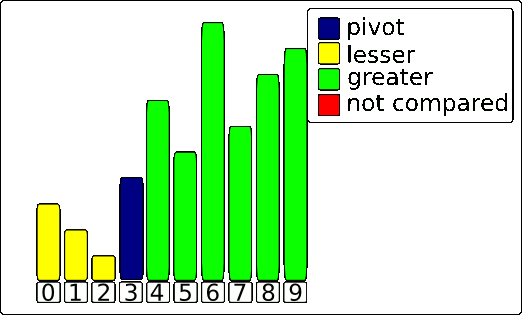
Subrotina Particiona

Subrotina Particiona

• Tempo de execução = $O(n)$, em que $n$ é o tamanho do (sub)vetor
• Custo $O(1)$ para cada elemento do (sub)vetor
• Claramente não usa memória extra (inplace), poi faz trocas repetidas no mesmo (sub)vetor

Corretude Particiona

• O laço mantém as invariantes:
  1. Todos os elementos de $A[inicio..i-1]$ são menores que o pivô $p$
  2. Todos os elementos de $A[i..j]$ são maiores que $p$
• Ao final do laço temos $A[inicio..i-1]$ menor que $p$ e $A[i..fim-1]$ maior que $p$
• Trocar $A[fim]$ com $A[i]$ coloca o último elemento na posição correta, e não altera o invariante já que $A[i]$ é maior que $p$.
• Ao final da execução, o (sub)vetor está pariticionado ao redor de $p$.

Corretude Quicksort

• Observe que A escolha do pivô não altera o funcionamento do algoritmo
• É possível usar o fato da corretude do usando indução
  • Caso base: quando $n_i=1$ o vetor está naturalmente ordenado
  • Hipótese: Supunha que QuickSort funciona para um vetor $1< m<n_i$ elementos, em que $n_i$ é o número de elmentos em $A[inicio..fim]$
  • Passo de indução: seja $x_i$ a posição do pivô ao final de Praticiona. O elemento em $A[x_i]$ estará na posição correta, e temos dois subvetores $A[inicio..x_i-1]$ e $A[x_i+1..fim]$, que são (recursivamente) ordenados por QuickSort (que pela Hipótese de indução, estão corretamente ordenados).
  • Portanto $A[inicio..x_i-1,x_i,x_i+1..fim]$ estará ordenado.
  • $A[1..x_0-1,x_0,x_0-1..n]$ em que $x_0$ é o primeiro pivô e $inicio$ e $fim$ corresponde ao vetor completo

Complexidade Quicksort

• A análise do QuickSort depende da escolha do pivô.
• No pior caso, EscolhePivo sempre retorna o maior (ou menor) elemento, de maneira que temos dois subvetores de tamanho $0$ e $n-1$. Nesse caso, a equação de recorrência é:
  $\begin{aligned} T(n) &=T(n-1)+n \\ &=T(n-2)+n+(n-1) \\ & \vdots \\ &=T(1)+\sum_{i=2}^{n-1} i \\ &=1+\frac{(n+1)(n-2)}{2} \\ &=\Theta\left(n^{2}\right) \end{aligned}$

Complexidade Quicksort

• No melhor caso, EscolhePivo sempre retorna a mediana , de maneira que temos dois subvetores de tamanho $n/2$. Nesse caso, a equação de recorrência é:
  $\begin{aligned} T(n) &= 2T\left(\frac{n}{2}\right)+n \\ &=\Theta\left(n \log n\right) \end{aligned}$

Complexidade Quicksort

• Em um caso intermediário, EscolhePivo divide o vetor original em duas partes de tamanho $pn$ e $(1-p) n$, em que $0 < p < 1$ é a proporção de elementos em uma das partições.

• Nesse caso, a equação de recorrência é:
  $T(n) = T\left(pn\right)+T\left((1-p)n\right)+n$

• Seja $k=p^{-1}$, podemos reescrever a recorrência como
  $T(n) = T\left(\frac{n}{k}\right)+T\left(\frac{k-1}{k}n\right)+n$

Complexidade Quicksort

• Nesse caso, podemos provar que $T(n) = O(n \log n)$

$\begin{aligned} T(n) &=T(n / k)+T((k-1) n / k)+n \\ & \leq c\left(\frac{n}{k} \log \left(\frac{n}{k}\right)\right)+\frac{n}{k}+c\left(\frac{(k-1) n}{k} \log \left(\frac{(k-1) n}{k}\right)\right)+\frac{(k-1) n}{k}+n \\ &=c\left(\frac{n}{k} \log \left(\frac{n}{k}\right)\right)+c\left(\frac{(k-1) n}{k}\left(\log (k-1)+\log \left(\frac{n}{k}\right)\right)\right)+2 n \\ &=c n \log n+n-c n \log k+\left(\frac{c(k-1) n}{k} \log (k-1)+n\right) \\ & \leq c n \log n+n \end{aligned}$

que é válida se $c > k/(\log k)$ pois nesse caso temos:

$c n \log k \geq\left(\frac{c(k-1) n}{k} \log (k-1)+n\right)$

Complexidade Quicksort

• Portanto, temos que QuickSort é $O(n \log n)$ se garantirmos que Particiona divide o vetor $A$ de tamanhos aproximadamente $n/k$ e $(k-1)n/k$
• Apesar de contraintuivo, podemos observar que o tamanho da árvore de recursão é $\log_{k/(k-1) n} n = \Theta(\log n)$, e em cada passo executamos algo proporcional a $n$
• Qualquer divisão que não deixe um subvetor vazio já seria boa o suficiente (assintoticamente falando)

Complexidade Quicksort

• O problema dessa análise ́e que ́e improvável que a partição
  seja sempre feita da mesma maneira em todas as chamadas recursivas.
• Vamos fazer uma análise probabilistica do algoritmo
• Para isso, vamos analisar o que acontece no caso medio, em que cada uma das $n!$ possíveis permutações dos elementos de $A$ tem a mesma chance de ser a ordenação do vetor de entrada $A$.

Complexidade Quicksort

• Seja $X_{a,b}$ uma variável aleatória que que indica se o elemento $x_a$ é comparado com o elemento $x_b$
  $X_{a,b}=\begin{cases} 1 &\text{se $x_a$ é comparado com $x_j$} \\ 0 &\text{se $x_a$ não é comparado com $x_j$} d \end{cases}$
• O número total de comparações é:

$\sum_{a=1}^{n-1}\sum_{b=a+1}^{n} X_{a,b}$

Complexidade Quicksort

• O valor médio esperado $E[X_{a,b}]$ dá uma estimativa do número médio esperado de comparações de $X_{a,b}$

$\begin{aligned}E[X_{a,b}] & = E\left[\sum_{a=1}^{n-1}\sum_{b=a+1}^{n} X_{a,b}\right]\\ & = \sum_{a=1}^{n-1}\sum_{b=a+1}^{n} E\left[ X_{a,b}\right]\\ & = \sum_{a=1}^{n-1}\sum_{b=a+1}^{n} (P_{a,b} = 1)\times 1 + (P_{a,b} = 0)\times 0 \\ & = \sum_{a=1}^{n-1}\sum_{b=a+1}^{n} (P_{a,b} = 1) \end{aligned}$

Complexidade Quicksort

• Recorde que no Quicksort, os elmentos são comparados apenas com o pivô. Após uma rodada de Particiona, o pivô migra para a posição final e não é mais comparado com ninguém.

• Portanto, podemos analisar a probabilidade de comparar dois elementos considerando as suas posições finais, relativamente à probabilidade de um elmento virar pivô em um determinado instante.

Complexidade Quicksort

• Seja $o_1, o_2, \cdots, o_n$ os elementos de $A$ em ordem (depois de ordenados), ou seja, $o_1 \leq o_2 \leq \cdots \leq o_n$

• Dados dois elementos quaisquer $o_a$ e $o_b$, $a<b$ eles são comparados (no máximo) uma única vez pois quando (qualquer) um deles for pivô.

• Ele é colocado na posição correta, e o outro estará a sua direita ou a sua esquerda, e o pivô não é comparado com mais ninguém.

Complexidade Quicksort

• Seja $P_{a,b}=1$ a probabilidade de comparar os elementos $o_a$ e $o_b$.
• Dado o subvetor $O[a..b] = [o_a,o_{a+1},\cdots,o_b]$, $P_{a,b}$ é igual a probabilidade de $o_a$ ou $o_b$ sejam escolhidos como pivô.
  • Se algum outro elemento $o_i$, $a<k<b$ for escolhido como pivô, então $o_a$ e $o_b$ vão para partes diferentes no final de Particiona com $o_i$ pivô, e nunca serão comparados
• Se qualquer elemento de $O[a..b]$ tiver igual probabilidade de ser selecionado como pivô, como temos $b-a+1$ elementos em $O[a..b]$, temos que

$(P_{a,b}=1) = \frac{2}{b-a+1}$

Complexidade Quicksort

• Substituindo na equação do valor experado temos que:

$\begin{aligned}E[X_{a,b}] & = \sum_{a=1}^{n-1}\sum_{b=a+1}^{n} (P_{a,b} = 1) \\ & = \sum_{a=1}^{n-1}\sum_{b=a+1}^{n} \frac{2}{b-a+1} \end{aligned}$

Complexidade Quicksort

• O valor médio esperado $E[X_{a,b}]$ dá uma estimativa do número médio esperado de comparações $X_{a,b}$ (se todas as permutações são igualmente prováveis)

• Portanto, no caso médio:

  $\begin{aligned}T(n) & = O(E(X_{a,b})) \\ & \leq c \sum_{a=1}^{n-1}\sum_{b=a+1}^{n} \frac{2}{b-a+1} \\ & < 2c n \sum_{k=i}^{n} \frac{1}{k} \\ \end{aligned}$

• É possivel provar que $\sum_{k=i}^{n} \frac{1}{k}$ é $O(\log n)$, poranto $T(n) = O(n \log n)$

Complexidade Quicksort

• Portanto, concluímos que o tempo medio de execução do Quicksort ́e $O(n \log n)$.

• Se, em vez de escolhermos um elemento fixo para ser o pivô, escolhermos um dos elementos do (sub)vetor com probabilidade uniforme, então uma análise análoga a que fizemos aqui mostra que o tempo esperado de execução dessa versão aleatória de Quicksort ́e $O(n \log n)$.

• Assim, sem supor nada sobre a entrada do algoritmo, garantimos um tempo de execução esperado de $O(n \log n)$.