Exemplo 1

• Considere que $T(n)= 3T(n/3)+1$ e queremos provar pelo método da substituição que ele é $O(n)$
• Temo que provar que $T(n) \leq cn$ para alguma constante positiva $c$, por indução em $n$
• No passo indutivo, temos:
  $\begin{aligned} T(n) &= 3T(n/3)+1 \\ & \leq cn +1 \end{aligned}$
• Entretanto, a nossa hipótese é que $T(n) \leq cn$, (e não $cn+1$, como obtivemos no passo indutivo)

Exemplo 1

• Isso não significa em $T(n) \neq O(n)$.
• O problema é que a expressão que usamos para provar nosso palpite não foi "forte" o suficiente. Vamos tentar provar que $T(n) \leq cn -d$, que contina sendo $O(n)$. No passo indutivo temos:

$\begin{aligned} T(n) &=3 T(n / 3)+1 \\ & \leq 3\left(\frac{c n}{3}-d\right)+1 \\ &=c n-3 d+1 \\ & \leq c n-d \end{aligned}$

• No caso base tesmo que $T(1)=1 \leq c-d$ sempre que $c \geq d+1$, portanto $T(n)=O(c n-d)=O(n)$

Exemplo 2

• Considere que $T(n)=T(\lfloor n / 2\rfloor+ 2)+1$ e queremos provar pelo método da substituição que ele é $O(\log n)$, assumindo o caso base $T(4)=1$

Exemplo 2

• É possível provar $T(n) \leq c \log n$, que no passo indutivo fica
  $\begin{aligned} T(n) &=T(\lfloor n / 2\rfloor+ 2)+1 \\ & \leq c \log \left(\frac{n}{2}+2\right)+1 \\ &=c \log \left(\frac{n+4}{2}\right)+1 \\ & \leq c \log (3 n / 2)-c+1 \\ &=c \log n-c(2-\log 3)+1 \\ & \leq c \log n \end{aligned}$
• em que a penúltima desigualdade vale para $n>8$ e a última para $c \geq 1 /(2-\log 3)$

Exemplo 2

• Entretanto, fortalecendo a hipótese indutiva para $T(n) \leq c \log (n-a)$, no passo indutivo temos
  $\begin{aligned} T(n) &=T(\lfloor n / 2\rfloor+ 2)+1 \\ & \leq c \log \left(\frac{n}{2}+2-a\right)+1 \\ &=c \log \left(\frac{n-a}{2}\right)+1 \\ &=c \log (n-a)-c+1 \\ & \leq c \log (n-a) \end{aligned}$

• em que a primeira desigualdade vale para $a\geq 4$ e a última para $c \geq 1$. Escolhendo $a=4$, $T(6)=T(5)+1=T(4)+2=3 \leq c \log (6-4)$ para $c\geq 3$. Portanto, fazendo $a=4$ e $c\geq 3$, temos que T(n) \leq c \log (n-a) para $n\geq 6$.

Fila de Prioridade

• Em algumas situações associamos uma prioridade a cada item coleção, e gostaríamos de ter acesso rápido ao item de maior prioridade

• É uma coleção dinâmica de elementos que possuem prioridades associadas e a operação de remoção deve sempre remover o elemento que possui maior prioridade.

• O termo prioridade é genérico: ter maior prioridade não significa necessariamente o maior valor.

  • Atendimento a idoso em um banco: maior idade $\rightarrow$ maior prioridade
  • Gerenciamento de estoque: menor quantidade de items $\rightarrow$ maior prioridade

Fila de Prioridade

• Filas de prioridades s ̃ao muito ́uteis na implementa ̧c ̃ao de diversos algoritmoscl ́assicos como:

  • Ordenação (HeapSort)

  • Busca heurística (Greed search, A*)

  • Compressão (Código de Huffman)

  • Grafos: caminhos mínimos (Dijkstra), árvore geradora mínima(Prim), Ordenação topológica (Dependência semântica)

  • União de Conjuntos (Union-find)

Operações

• Constrói uma fila de prioridade a partir de um conjunto

• Insere elemento na fila

• Remove elemento com maior prioridade

• Alteração da prioridade de um elemento

Vetores ordenados

• Uma maneira de dar suporte a essas operações é usar um vetor ordenado

  • Contrução: $\mathcal{O}(n \log n)$,
  • Inserção/Alteração de prioridade: $\mathcal{O}(n)$
  • Remoção: $\mathcal{O}(1)$

Heap

• Uma outra alternativa é usar Heaps

  • Construção: $\mathcal{O}(n)$,
  • Inserção/Alteração de prioridade: $\mathcal{O}(\log n)$
  • Remoção: $\mathcal{O}(\log n)$

Heap

• Heap pode ser entendida com uma árvore
  • quase completa:
    • Todos os níveis exceto o último devem estar totalmente preenchidos.
    • Se o seu último nível não estiver preenchido, os nós devem estar preenchidos da esquerda para a direita.
  • satisfaz a propriedade heap:
    • Um nó deve ter prioridade maior ou igual à prioridade de seus filhos, se eles existirem.

Heap

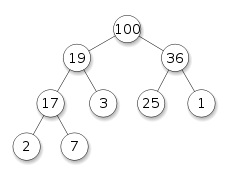
Heap

• No entanto, heaps são normalmente implementadas em um vetor

• Nesse caso, para uma determinada posição $i$

  • $pai(i) = \lfloor \frac{i}{2} \rfloor$

  • $filhoEsquerdo(i) = 2*i$

  • $filhoDireito(i) = 2*i + 1$

  • (obs): $\frac{i}{2}$ e $2*i$ podem ser implementados de maneira eficiente usando bit shifts

Heap

Heap

• No caso de índice começando em zero, para uma determinada posição $i$

  • $pai(i) = \lfloor \frac{i-1}{2} \rfloor$

  • $filhoEsquerdo(i) = 2*i + 1$

  • $filhoDireito(i) = 2*i + 2$

Construção do Heap

• Um vetor ordenado é pela priopridade é um Heap

• Um problema é que ordenar o vetor tem custo de (pelo menos) $\mathcal{O}(n \log n)$

• No entanto, o vetor não precisa estar completamente ordenado... somente os caminhos da "raíz" (primeiro nível) até as "folhas" (último nível) é que precisa estar ordenado

Construção da HEAP

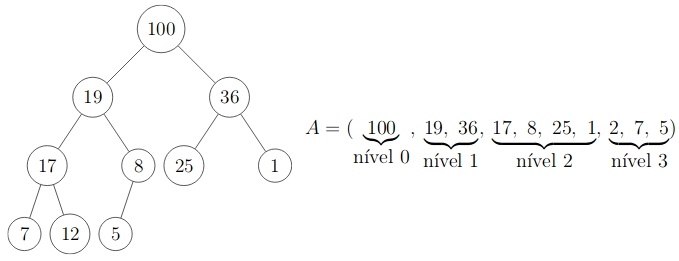
Corrige Heap Descendo

• Suponha que um determinada subárvore cuja raíz é $H[i]$ viola a propriedade heap (isto é, sua prioridade é menor que a de (pelo menos um) seus filhos)

• Entretanto, as subárvores filhas $H[2i]$ e $H[2i+1]$ são heap.

• Podemos corrigir a heap "descendo" o elmento $H[i]$:

  • Trocar $H[i]$ com o filho de maior prioridade
  • Chamar recursivamente CorrigeDescendo para o filho trocado (pois a propriedade Heap pode continuar violada para ele)

Corrige Heap Descendo

• Exemplos de CorrigeHeapDescendo(H,2)

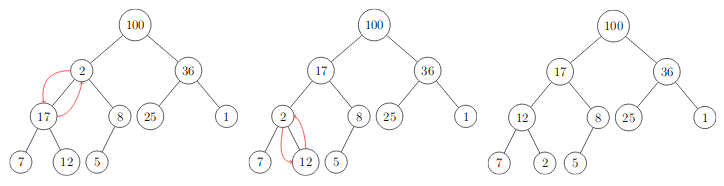
Corrige Heap Descendo

Corretude: Corrige Heap Descendo

Seja $h_x = \lfloor \log(n/x) \rfloor$ a altura do nó que está na posição $x$

• Caso Base: $h_i = 0$ o nó é uma folha, portanto não tem filhos e a propriedade heap é válida
• Hipótese: Se $H[2k]$ e $H[2k+1]$ são heaps, CorrigeHeapDescendo($H,k$) restaura a Heap para todo nó de altura $h_k < h_i$
  • Se H[i] tem prioridade maior que seus filhos, o algoritmo não faz nada pois a proriedade heap já é valida. Temos que mostrar por indução que CorrigeHeapDescendo($H,i$) está correto
  • Se a prioridade de $H[i]$ é menor que um de (pelo menos um de) seus filhos, o algoritmo troca $H[i]$ com o maior deles, e chama recursivamente CorrigeHeapDescendo($H,maior$). Como a altura do filho é menor que a do pai, pela Hipótese de indução, $H[i]$ agora é uma haep.

Complexidade: Corrige Heap Descendo

• CorrigeHeapDescendo($H,i$) tem um tempo proporcional a altura de $i$, ou seja $O(\log (n-i))$.

• No pior caso, i é a raiz da árvore, então a complexidade é proporcianal a altura da árvore

• Como a heap é uma árvore binária quase completa, sua altura é $O(\log n)$.

• Portanto, a complexidade de CorrigeHeapDescendo é $O(\log n)$

ConstroiHeap

• Considere que temos um vetor qualquer (não heap), e queremos transformá-lo em uma heap

• Podemos transformá-lo em uma haep utilizando CorrigeHeapDescendo como uma subrotina:

  • Observe que os nós folhas são heap (não tem filhos).
  • Podemos chamar CorrigeHeapDescendo para os nós não folha, começando pelo primeiro elemento não folha $H\lfloor n/2 \rfloor$ até o raíz $H[1]$

ConstroiHeap

ConstroiHeap

• É fácil mostrar que ConstroiHeap funciona, já que ele faz suscessivas chamadas a CorrigeHeapDescendo

• A invariante de laço é que a cada iteração do laço para indexado por $i$, para todo $j$ tal que $i+ 1\leq j\leq n$ , a ́arvore enraizada em $H[j]$ e um heap.

• Como CorrigeHeapDescendo é excutado $H\lfloor n/2 \rfloor$ até $H[i]$, a invariante de laço se mantém e por indução podemos provar que ConstroiHeap constrói uma heap para qualquer vetor.

ConstroiHeap: Complexidade

• Uma análise preliminar, podemos constantar que ConstroiHeap tem complexidade $O(n \log n)$, uma vez CorrigeHeapDescendo tem complexidade $O(\log n)$ e ele é executado $\lfloor n/2 \rfloor$ vezes, que é $O(n)$

• Entretanto, observe que $O(\log n)$ é um limite superior para a complexidade de ConstroiHeap. Na verdade sua complexidade é proporcianal à algura do elemente $i$, ou seja, $O(\log (n-i))$.

• Podemos usar esse fato para encontrar uma complexidade mais justa para o ConstroiHeap

ConstroiHeap: Complexidade

• Uma estimativa quantidade de nós em uma dada altura $h$ da heap é $\lceil \frac{n}{2^{h+1}} \rceil$.
• Podemos escrever a complexidade do ConstroiHeap como:
  $\begin{aligned} T(n) &=\sum_{h=0}^{\log(n)}\left\lceil\frac{n}{2^{h+1}}\right\rceil \times O(h) \\ &=O\left(n \times \sum_{h=0}^{\lg (n)} \frac{h}{2^{h}}\right) \\ &=O\left(n \times \sum_{h=0}^{\infty} \frac{h}{2^{h}}\right) \end{aligned}$

ConstroiHeap: Complexidade

• Observe que para $i \geq 1$, $\left((i+1) / 2^{i+1}\right) /\left(i / 2^{i}\right)<1$ .

$\begin{aligned} T(n) &= O\left(n \times \sum_{h=0}^{\infty} \frac{h}{2^{h}}\right)\\ & \leq cn \\ & = O(n) \end{aligned}$

Remover item da heap

• Uma outra operação da heap é a remoção do item de maior prioridade
• Observe que o primeiro elmento da heap é o item de maior prioridade. Então acessá-lo é $O(1)$
• Para a remoção, precisamos colocar outro elmento no lugar.
• Uma alteração que mexe o mínimo possível na Heap é trocar o primeiro com o último elemento.
• Podemos então usar CorrigeHeapDescendo($H,1$) para corrigir a heap

RemoveDaHeap

Complexidade e Corretude de RemoveDaHeap

• Observe que RemoveDaHeap viola apenas a propriedade heap do nó raiz, já que o último elemento é uma folha e não mexemos em outras posições da heap.

  • CorrigeHeapDescendo($H,1$) restaura a propriedade heap, portanto RemoveDaHeap está correto

• A complexidade é dominada por CorrigeHeapDescendo($H,1$), já que a troca é $O(1)$. Portanto, a complexidade é $O(\log n)$

Inserir elemento na heap

• Caso haja espaço na heap, uma estratégia é inserir na primeira posição disponível
• Obviamente, isso pode violar propriedade heap
• No entanto, antes da inserção, a propriedade heap está mantida.
• O procedimento CorrigeHeapSubindo pode ser usado para restaurar a priopridade heap

CorrigeHeapSubindo

• Dada uma posição $H(i)$, se a prioridade de $H(i)$ é maior que a de seu pai, podemos trocar $H(i)$ com o seu pai.
• A propriedade heap das subárvores está restabelecida, mas eventualmente é preciso continuar subindo até chegar ao nó raiz.

CorrigeHeapSubindo

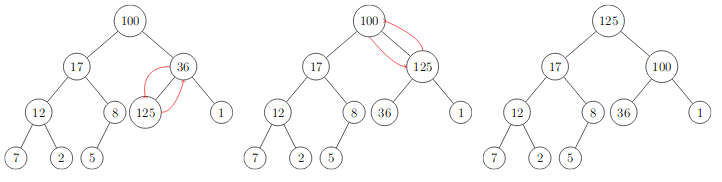
CorrigeHeapSubindo

Complexidade e Corretude do CorrigeHeapSubindo

• Um argumento similar ao usado para CorrigeHeapDescendo pode ser usado para demonstrar por indução que CorrigeHeapSubindo está correto

• De maneira similar, podemos mostrar que a complexidade de CorrigeHeapSubindo é $O(n \log n)$

InserirNaHeap

Complexidade e Corretude de RemoveDaHeap

• Observe que InserirNaHeap viola apenas a propriedade heap do último nó, já que não mexemos em outras posições da heap.

  • CorrigeHeapSubindo($H,1$) restaura a propriedade heap, portanto InserirNaHeap está correto

• A complexidade é dominada por CorrigeHeapSubindo, já que a inserção é $O(1)$. Portanto, a complexidade é $O(\log n)$

Altera prioridade de um elemento

• Para alterar a prioridade de um elemento, podemos usar CorrigeHeapSubindo ou CorrigeHeapDescendo, dependendo se a prioridade do elemento $i$ subiu ou desceu
  • Se a prioridade cresceu, chamar CorrigeHeapSubindo($H,i$)
  • Se a prioridade desceu, CorrigeHeapDescendo($H,i$)

AlteraHeap

Complexidade e Corretude de AlteraHeap

• Como AlteraHeap é baseado em CorrigeHeapSubindo e CorrigeHeapDescendo, podemos concluir que ele está correto, e que a sua complexidade é $O( \log n)$

Selection Sort

• Uma estratégia simples para ordenar vetor é:

  • Percorrer o vetor e encontrar o máximo
  • Trocar o último elemento pelo máximo
  • Repetir o processo, considerando o vetor com tamanho $n-1$

• Essa estratégia é conhecida como como Selecion Sort

Selection Sort

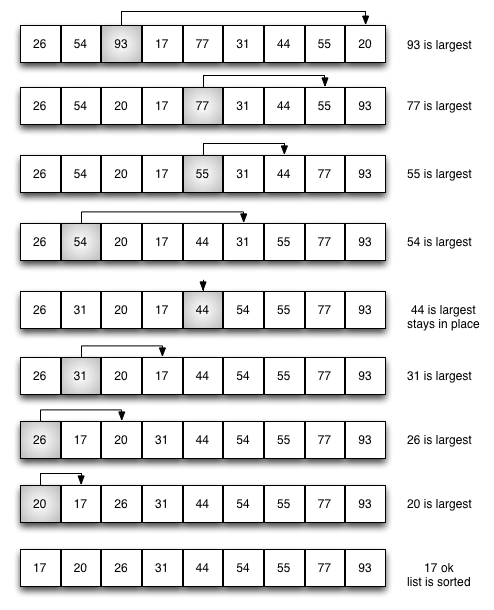
Selection Sort

Selection Sort

• A análise de corretude do selecion sort é similar a do heap sort (veremos mais adiante), assumindo que o algoritmo que seleciona o máximo funciona

• A complexidade é $O(n^2)$

Heap Sort

• Podemos usar uma Heap para ordenar um vetor

  • A ideia é construir uma Heap com o vetor, e trocar o último elemento com o primeiro, rafazendo-se a Heap com tamanho $n-1$

  • Repete-se esse processo até ter o vetor ordenado

Heap Sort

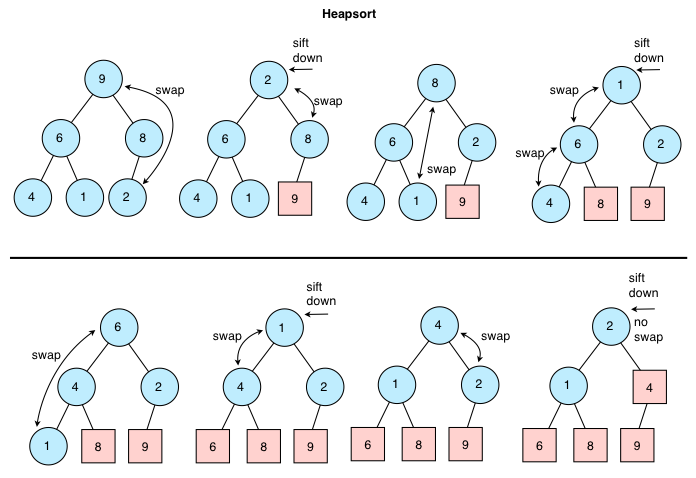
Heap Sort

Corretude do Heap Sort

• Antes de cada iteração $i$ do laço para, temos que:

  • O subvetor $A[i+1..n]$ contém os $n-i+1$ elmentos de $A$ em ordem crescente
  • O subvetor $A[1..i]$ é uma heap

• No início da iteração $i$, HeapSort troca $A[1]$ (que por definição é o maior elemento da Heap) com $A[i]$, e diminui o tamanho da heap em 1. - $A[i]$ é menor que os elementos $A[i+1..n]$, portanto $A[i..n]$ continua ordenado.

• Sabemos que CorrigeHeapDescendo($A,1$), está correto. Portanto a propriedade se mantém, e podemos provar por indução que HeapSort está correto

Heap Sort

• Heap Sort tem complexidade $O(n \log n)$ (cada chamada para refazer a heap tem custo $O(\log n)$, e é chamada $n$ vezes).

• Além disso, também há o custo adicional de construir a heap $\mathcal{O}(n)$.

• A ordem original dos elementos iguais pode mudar, portanto ele não é estável