Análise de Algoritmos
Ronaldo Cristiano Prati
Bloco A, sala 513-2
ronaldo.prati@ufabc.edu.br
Grafos
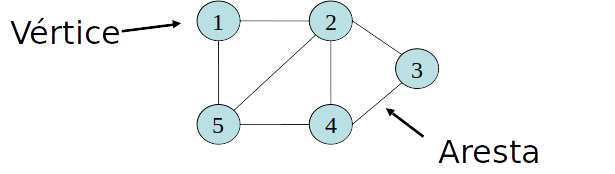
- Um grafo G=(V,E) consiste em um conjunto de vértices V
e um conjunto de arestas E. - Cada aresta corresponde a um par de vértices
Grafos
-
Vértices são objetos, e arestas modelam relacionamento. Por exemplo, um grafo pode modelar redes de pessoas, e os vértices são as relações de amizade (grafo de amizade).
-
Nota: Algumas definições não permitem ligações com o mesmo vértice (self-loops). Nesse caso, os grafo são chamados de grafos simples
-
Grafos podem ser de dois tipos: direcionados e não direcionados
Grafo Direcionado
- Grafo direcionados (digrafo): E é um conjunto de pares ordenados (também chamados de arcos) (u,v) em que u,v∈V
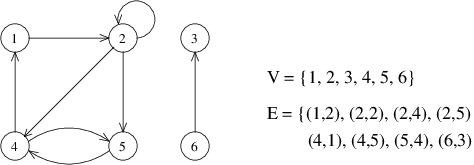
Grafo não-Direcionado
- Grafo não-direcionados: E é um conjunto de pares não ordenados de vértices {u,v} em que u,v∈V
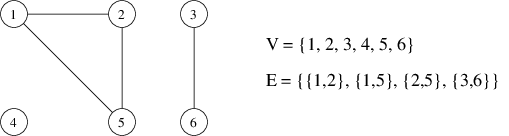
Grafos ponderados
- Frequentemene as arestas (u,v) em um grafo tem pesos w(u,v), e.g.
- Malha rodoviária (distâncias)
- Redes de cabos (capacidade)
Grafos (exemplos)
- Grafos aparecem em vários problemas e diferentes aplicações
- Por exemplo, no grafo de amizades em que vértices são pessoas e arestas são amizades, alguns problemas que queremos responder:
- Ele é direcionado ou não-direcionado? (se eu te considero o meu amigo, isso significa que você é meu amigo?)
- Duas pessoas quaisquer são amigas? Se não, quão próximas elas são?
- Eu estou ligado por uma cadeia de amigos a uma estrela do cinema? Quão perto eu estou dessa estrela?
- Exite um caminho entre quaisquer duas pessoas em um grafo?
- Quem tem mais amigos?
- Qual é a maior comunidade, em que todos são amigos (maior clique)?
Terminologia - Grau
- Aresta (u,v) é dita ser incidente a u e v
- Grafo não-direcionado: Grau de um vértice é o número de vértices incidentes a eles.
- Grafo Direcionado: Grau de entrada/saída de um vértice é o número de arestas entrando/saindo de um vértice.
Terminologia - Passeio
-
Passeio: um passeio é uma sequência não vazia de vértices P=(v0,v1,v2,⋯,vk) tal que (vi,vi+1)∈E (ou {vi,vi+1}∈E)
- v0 e vk são o início e fim de P
- v1,v2,⋯,vk−1 são vértices internos de P
- V(P) é o conjunto dos vértices de P
- E(P) é o conjunto de arestes de P
-
Se existe um passeio entre dois vértices v0 e vk, dizemos que os vértices e arestas do passeio são alcançáveis a partir de v0.
-
O comprimento de P é a quantidade de arestas de P
Terminologia
-
Trilha: um passeio que não tem arestas repetidas é chamado de trilha
-
Caminho: um passeio que não tem vértices repetidos (exceto possivelmente o primeiro e o último) é chamado de caminho
-
Ciclo: um caminho cujo início e fim é o mesmo vértice é chamado de ciclo
Terminologia
-
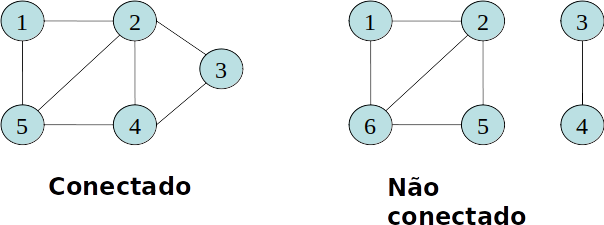
Um grafo é conectado se todo par de vértices é ligado por um caminho
-
Os subgrafos conexos de um grafo desconexo que são maximais com respeito a conectividade são chamadas de componentes conexas
Terminologia
-
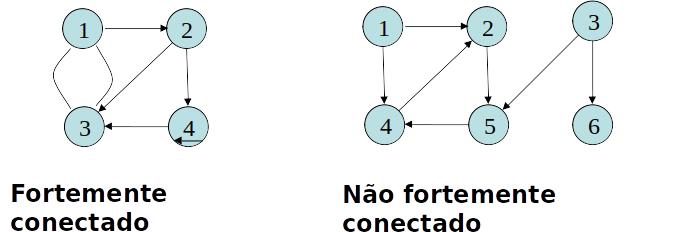
Um grafo direcionado é fortemente conectado se todo o par de vértices é ligado por um caminho
-
Os componentes fortemente conectados de um grafo direcionado são conjuntos de vértices sob a relação “são mutuamente alcançáveis”.
Grafos - Representação
-
Existem diversas representações que podem ser utilizadas. As duas mais comuns são:
-
Um grafo pode ser representado por:
-
lista de adjacênia
- Vetor de tamanho ∣V∣ em que cada elemento é uma lista de arestas incidentes em cada vértice.
-
matriz de adjacência
- Matriz de tamanho ∣V∣×∣V∣ em que cada célula representa uma aresta
-
Grafos - Lista de adjacênia
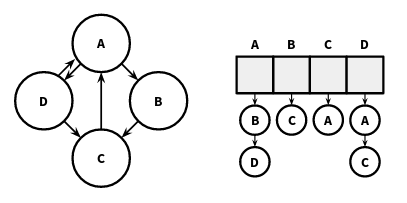
- Para grafos não direcionados, cada nó é representado duas vezes.
- Se o grafo é ponderado, o peso é armazenado juntamente com cada aresta.
Grafos - Matriz de adjacênia
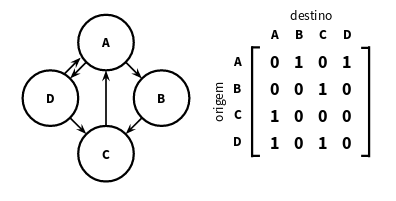
Grafos - Matriz de adjacênia
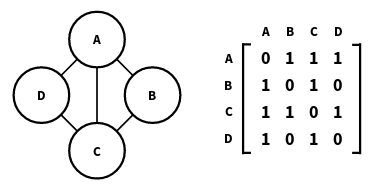
- Para grafos não direcionados, a matriz de adjacênia é simétrica ao longo da matriz diagonal (AT=A)
- Se o grafo é ponderado, pesos são armazenados ao invés de 1's
Grafos - Representação
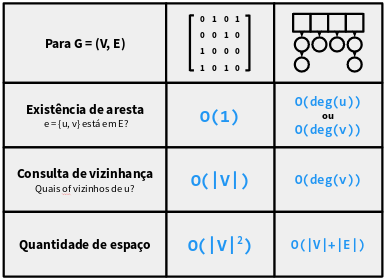
Grafos - Representação
-
A representação por lista de adjacência é boa se o grafo é esparso (∣E∣<<∣V∣2)
-
Já a representação por matriz de adjacência é boa se o grafo é denso (∣E∣≈∣V∣2)
-
No curso, vamos assumir a representação baseada em lista de adjacência (a não ser que indicado), uma vez que os grafos grandes tendem a ser esparsos.
Busca em Grafos
- Dado um grafo G=(V,E) e um vértice s∈V, deseja-se encontrar todos os vértices em G que estão conectados a v.
- Em geral, esses algoritmos tem um conjunto de nós não descobertos, descobertos mais ainda não completamente explorados, e completamente examinados.
- Serão vistas duas maneiras de realizar essa tarefa:
- Busca em profundidade, e;
- Busca em largura.
- Eles se diferem na ordem em que os nós são explorados.
Busca em profundidade
- A busca em profundidade (depth-first search) é um algoritmo para caminhar no grafo.
- A estratégia é buscar o vértice mais profundo no grafo sempre que possível.
- As arestas são exploradas a partir do vértice u mais recentemente descoberto que ainda possui arestas não exploradas saindo dele.
Busca em profundidade
- Quando todas as arestas adjacentes a s tiverem sido exploradas a busca anda para trás para explorar vértices que saem do vértice do qual s foi descoberto.
- O algoritmo é a base para muitos outros algoritmos importantes, tais como verificação de grafos acíclicos, ordenação topológica e componentes fortemente conectados (como veremos na próxima aula).
Busca em profundidade

Busca em profundidade

Busca em profundidade
- Para acompanhar o progresso do algoritmo cada vértice é "colorido" de branco, cinza ou preto.
- Todos os vértices são inicialmente brancos (não descobertos).
- Quando um vértice é “descoberto” pela primeira vez ele torna-se cinza (é colocado na pilha),
- Torna-se preto quando seus adjacentes tenham sido completamente examinados (sai da pilha).
Busca em profundidade
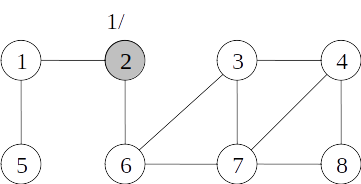
Busca em profundidade
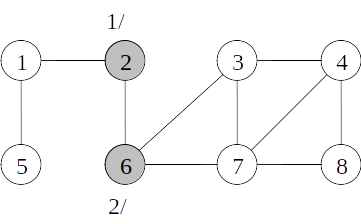
Busca em profundidade
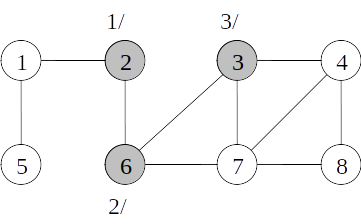
Busca em profundidade
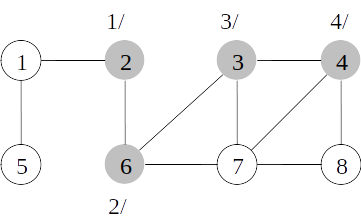
Busca em profundidade
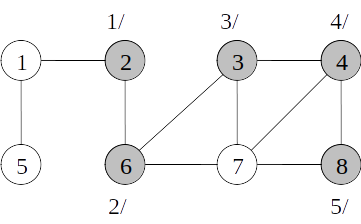
Busca em profundidade
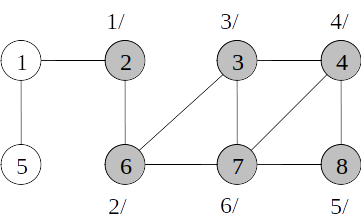
Busca em profundidade
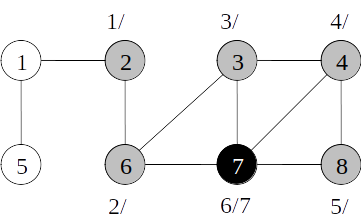
Busca em profundidade
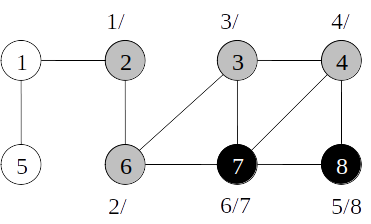
Busca em profundidade
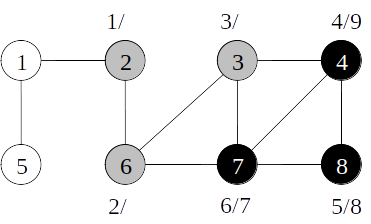
Busca em profundidade
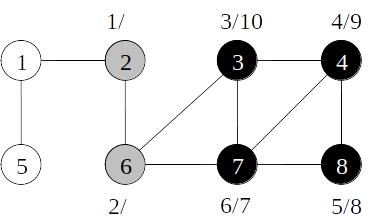
Busca em profundidade
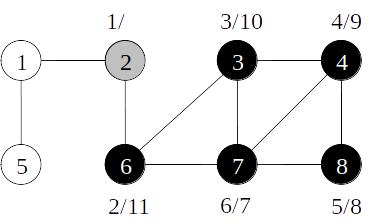
Busca em profundidade
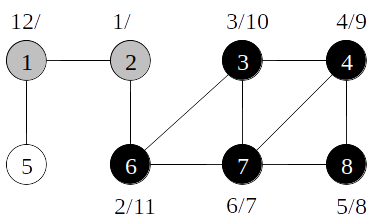
Busca em profundidade
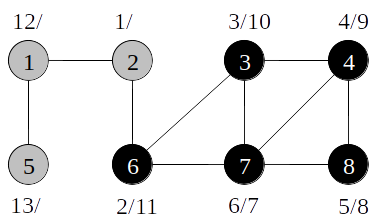
Busca em profu2didade
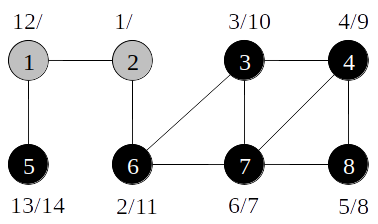
Busca em profundidade
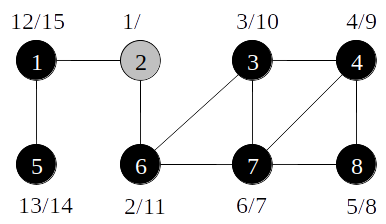
Busca em profundidade
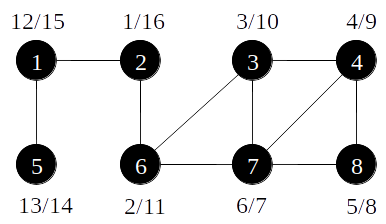
Busca em profundidade - complexidade
- A complexidade da busca depende da estrutura de dados utilizada.
- Quando uma matriz de adjacências é utilizada, encotrar os vizinhos de um nó requer O(∣V∣). Como ele é feito para todos os vértices, busca em profundidade requer O(∣V∣2).
- Quando uma lista de adjacências é utilizada, encontrar os vizinhos requer O(∣E∣) e a busca profundidade requer O(∣V∣+∣E∣)
Busca em Largura
- A busca em largura (breadth-first search) expande a fronteira entre vértices descobertos e não descobertos uniformemente através da largura da fronteira.
- O algoritmo descobre todos os vértices a um distância k do vértice origem antes de descobrir qualquer vértice a uma distância k+1.
Busca em Largura
- Assim como na busca em profundidade, cada vértice é "colorido" de branco, cinza ou preto.
- Todos os vértices são inicialmente brancos.
- Quando um vértice é “descoberto” pela primeira vez ele torna-se cinza (entra na fila).
- Vértices cinza e preto já foram “descobertos”, mas são distinguidos para assegurar que a busca ocorra em largura.
Busca em largura

Busca em largura
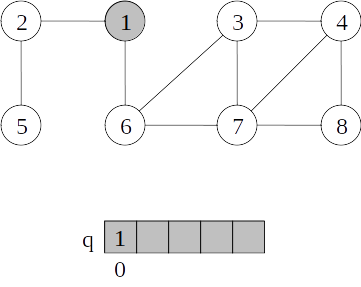
Busca em largura
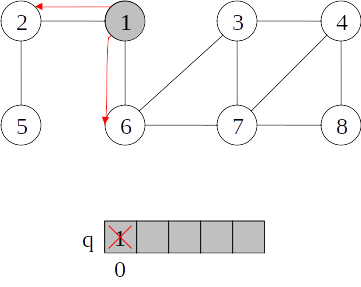
Busca em largura
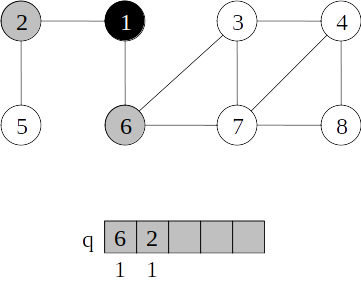
Busca em largura
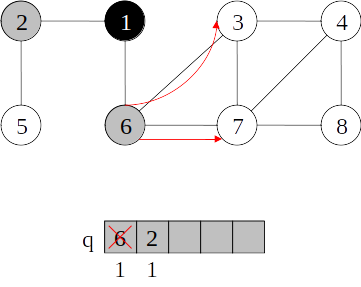
Busca em largura
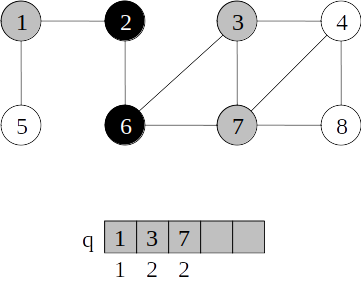
Busca em largura
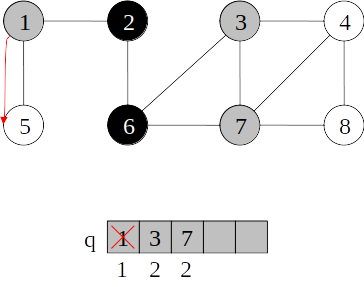
Busca em largura
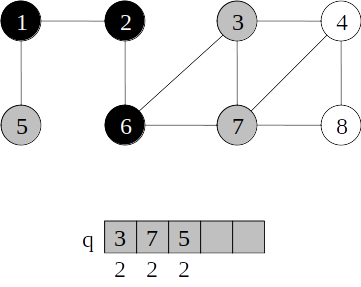
Busca em largura
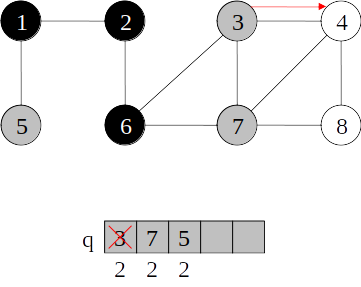
Busca em largura
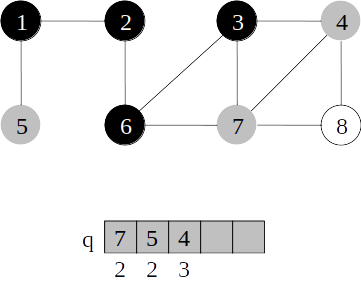
Busca em largura
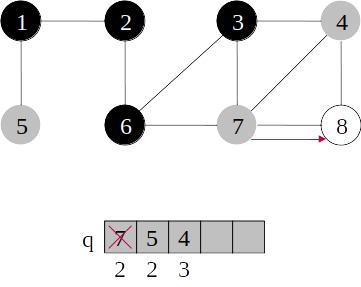
Busca em largura
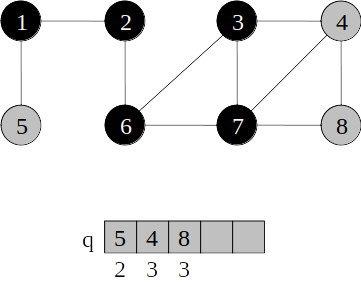
Busca em largura
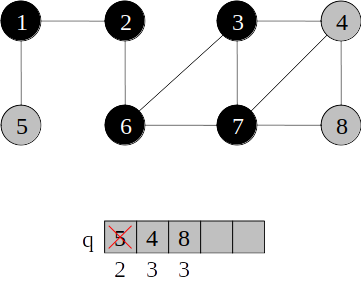
Busca em largura
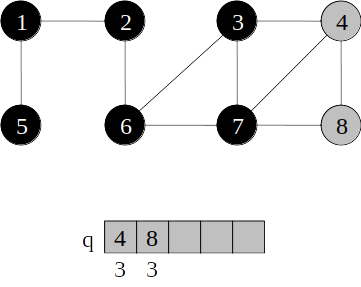
Busca em largura
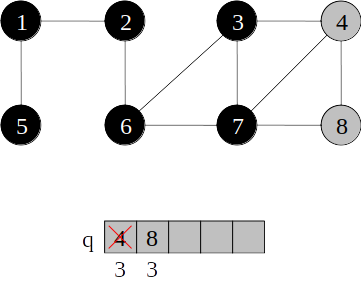
Busca em largura
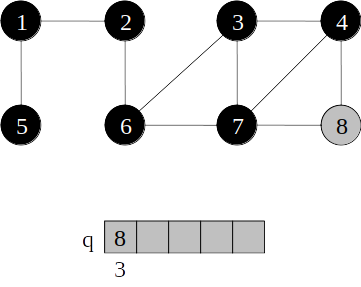
Busca em largura
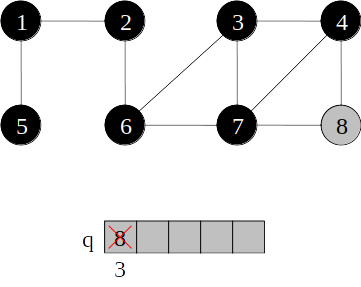
Busca em largura
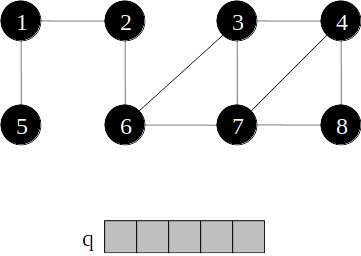
Busca em largura
- Assim como a busca em profundidade, a complexidade da busca em largura depende da estrutura de dados utilizada
- Cada vértice entra na fila q exatamente uma vez, portanto o laço enquanto faz ∣V∣ iterações.
- Se uma matriz de adjacências é utilizada, é necessário O(∣V∣) para encontrar os vizinhos de cada nó visitado. O tempo total é O(∣V∣2).
- Se lista de adjacências é utilizada, o custo do laço é O(∣V∣+∣A∣).