def sigmoid(z):
return(1 / (1 + np.exp(-z)))
def predict(theta, X, threshold=0.5):
p = sigmoid(X.dot(theta.T)) >= threshold
return(p.astype('int'))
def costFunction(theta, X, y):
m = y.size
h = sigmoid(X.dot(theta))
J = -1*(1/m)*(np.log(h).T.dot(y)+np.log(1-h).T.dot(1-y))
if np.isnan(J[0]):
return(np.inf)
return(J[0])
def gradient(theta, X, y):
m = y.size
h = sigmoid(X.dot(theta.reshape(-1,1)))
grad =(1/m)*X.T.dot(h-y)
return(grad.flatten())
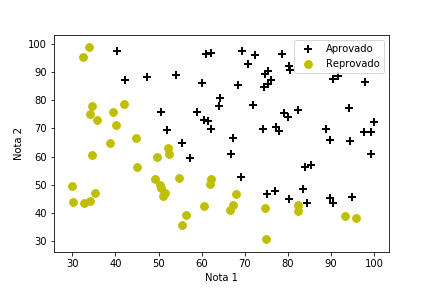
- Notas de duas avaliações
- Aprovação segue regra não linear
import pandas as pd
import numpy as np
from scipy.optimize import minimize
data = np.array(pd.read_csv("ex2data1.txt",sep=",",header=None))
X = np.c_[np.ones((data.shape[0],1)), data[:,0:2]]
y = np.c_[data[:,2]]
initial_theta = np.zeros(X.shape[1])
cost = costFunction(initial_theta, X, y)
grad = gradient(initial_theta, X, y)
print('Cost: \n', cost)
print('Grad: \n', grad)
res = minimize(costFunction, initial_theta,
args=(X,y), method=None, jac=gradient, options={'maxiter':400})
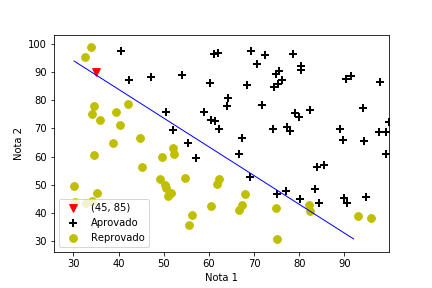
- Notas de duas avaliações
- Aprovação segue regra não linear
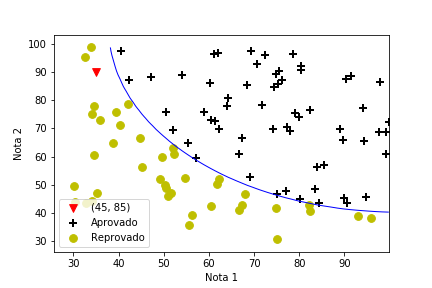
- Incorporando termos quadráticos aos dados
X = np.c_[np.ones((data.shape[0],1)), data[:,0:2], data[:,0:2]**2 ]
y = np.c_[data[:,2]]
initial_theta = np.zeros(X.shape[1])
cost = costFunction(initial_theta, X, y)
grad = gradient(initial_theta, X, y)
print('Cost: \n', cost)
print('Grad: \n', grad)
res = minimize(costFunction, initial_theta,
args=(X,y), method=None, jac=gradient, options={'maxiter':400})
- Notas de duas avaliações
- Aprovação segue regra não linear
def costFunctionReg(theta, reg, *args):
m = y.size
h = sigmoid(XX.dot(theta))
J = -1*(1/m)*(np.log(h).T.dot(y)+np.log(1-h).T.dot(1-y)) +
(reg/(2*m))*np.sum(np.square(theta[1:]))
if np.isnan(J[0]):
return(np.inf)
return(J[0])
def gradientReg(theta, reg, *args):
m = y.size
h = sigmoid(XX.dot(theta.reshape(-1,1)))
grad = (1/m)*XX.T.dot(h-y) + (reg/m)*np.r_[[[0]],theta[1:].reshape(-1,1)]
return(grad.flatten())
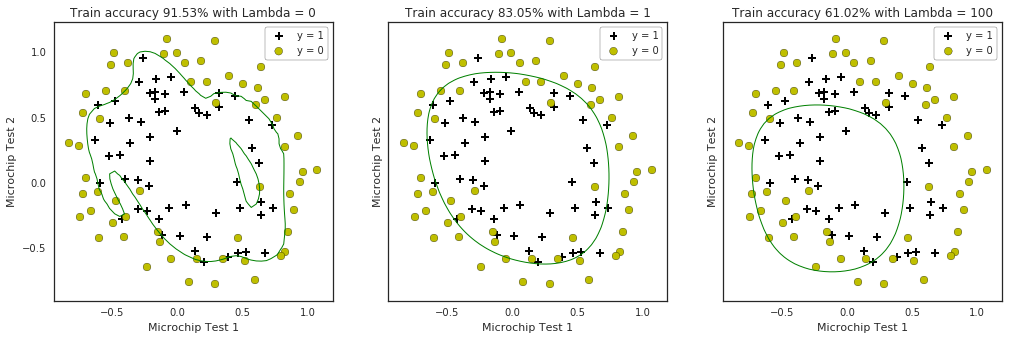
- Resultados de dois testes
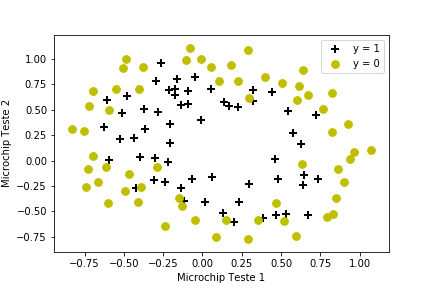
Acrescentando termos
- Vamos criar atritubtos de grau 6
from sklearn.preprocessing import PolynomialFeatures
poly = PolynomialFeatures(6)
XX = poly.fit_transform(data2[:,0:2])
XX.shape
- Vamos testar com 3 valores de λ
initial_theta = np.zeros(XX.shape[1])
costFunctionReg(initial_theta, 1, XX, y)
for i, C in enumerate([0, 1, 100]):
res2 = minimize(costFunctionReg, initial_theta,
args=(C, XX, y), method=None, jac=gradientReg,
options={'maxiter':3000})
- Teste com diferentes valores de λ