Problema Exemplo

Baseado nesses dados, se temos uma casa de 750 $ft^2$, qual seria o preço de venda?

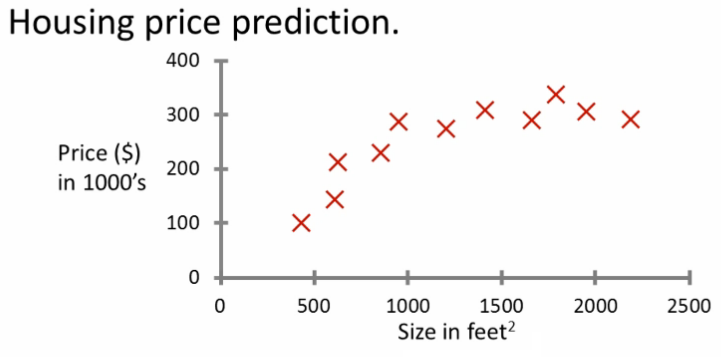
Problema Exemplo

• Que abordagem podemos usar para resolver o problema?
  • Uma linha reta pelos dados?
    Talvez $150 000
  • Um polinômio de segunda ordem?
    Talvez $200 000
• Como escolhemos entre uma linha reta ou uma curva?
• Cada uma dessas abordagens representa uma maneira diferente de aprendizado supervisionado

Problema Exemplo

• Qual é a ideia geral?
  • Fornecemos ao algoritmo um conjunto de dados com a "resposta correta"
  • Para esse conjunto, nós sabemos qual é o preço real das casas
  • A ideia é que podemos aprender a relação entre o preço e a metragem a partir do conjunto de treino
  • O algoritmo deve então prover qual é a resposta para novos dados que não sabemos o preço ainda
  • Esse problema é chamado de regressão

Outro exemplo

Podemos predizer o tipo de tumor de mama como maligno ou benigno baseado no tamanho do tumor?

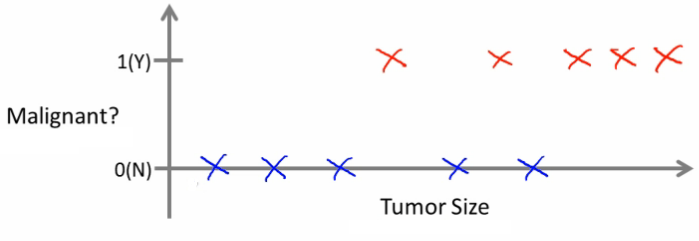
Outro exemplo

Analizando os dados:

• Cinco de cada tipo
• Podemos estimar o tipo de tumor baseado do seu tamanho?
• Esse é um problema de classificação
• Classificar os dados em uma das duas classes discretas: maligna ou benigna
• Em problemas de classificação, também podemos ter mais de duas classes:
• 0 - benigno
• 1 - Tipo 1
• 2 - Tipo 2
• 3 - Tipo 3

Outro exemplo

• Também podemos ter mais de um atributo. Por exemplo, podemos usar o tamanho do tumor e a idade do paciente

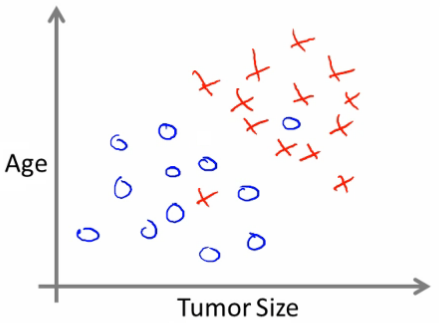
Outro exemplo

• Podemos tentar definir a separação entre as classes desenhando uma linha reta entre os dois grupos
• Também podemos criar uma função mais complexa para cada um dos grupos (veremos exemplos mais afrente no curso)
• Então, quando tivermos um novo indivíduo com um tumor de certo tamanho e com uma certa idade, podemos usar essa informação para prever o tipo de tumor

Outro exemplo

Também podemos considerar outros atributos:

• Expessura da aglomeração das células
• Uniformidade do tamanho da célula
• Uniformidade to formato da célula

Alguns algoritmos tem a capacidade de lidar com um número infinito de atributos! Para isso, usamos um truque matemático das SVMs (que iremos tratar mais adiante).

Agrupamento - Exemplos

Dados de Microarray

• Dados um grupo de individuos
• Para cada um, medir a expressão de alguns genes
• Rodar um algoritmo de agrupamento para agrupar indivídos em tipos de pessoas

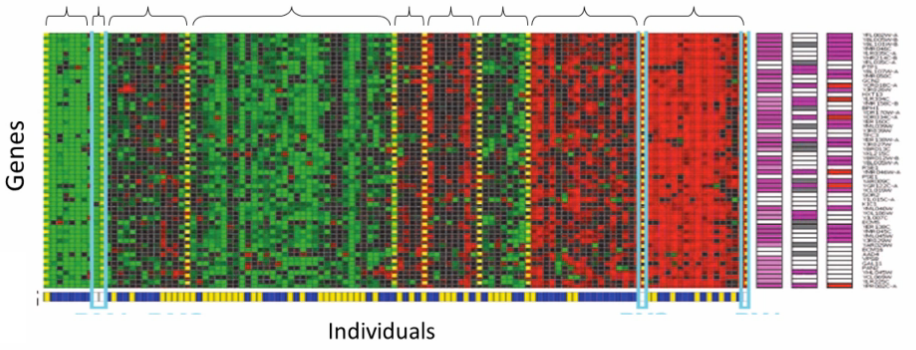
Agrupamento - Exemplos

• Google news
  Agrupar noticias em grupos correlatos
• Organizar clusters de computadores
  Identificar pontos fracos em potencial ou redistribuir as terefas eficientemente
• Análise de redes sociais
  Grupos de consumo em potencial
• Dados atronômicos
  Agrupar informações para descobrir novos sistemas planetários

Regressão Linear

• Problema do preço das casas usado anteriormente
• Problema de aprendizado supervisiondo de regressão
• Por onde começamos?
  • Conjunto de treinamento
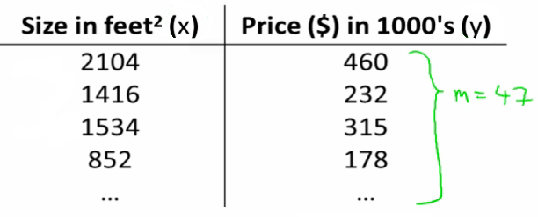
  • Notação (usada durante o curso):
    $m$ = número de exemplos de treinamento
    $x$ = variáveis de entrada
    $y$ = variável de saída (variável meta)
    $(x,y)$ = um exemplo de treinamento (genérico)
    $(x_i,y_i)$ = um exemplo de treinamento específico
    $i$ é um índice do conjunto de treinamento

Regressão Linear

Regressão Linear

• Com o nosso conjunto de treino definido, como o usamos?
  • Pegamos o conjunto de Dados
  • Usamos ele para alimentar um algoritmo de aprendizado
  • Algoritmo dá como saída uma função (denotada $h$, de hipótese)
  • Essa função tem como entrada um novo dado (por exemplo, o tamanho de uma nova casa)
  • E gera como saída uma estimativa do valor de $y$

Regressão Linear

• Vamos representar a hipótese $h$ por

$h_\theta(x) = \theta_0 + \theta_1 x$

• O que isso significa?
  $y$ é uma função linear de $x$!
• $\theta_i$ são parâmetros:
  • $\theta_0$ e o termo independente
  • $\theta_1$ é o gradiente
• Esse tipo de função é uma regressão linear com uma única variável, também chamada de regressão linear univariada.

Em resumo

• Uma hipótese é criada sobre as variáveis de entrada
• Usa parâmetros para determinar o sistema de Aprendizado
• Dá como saída uma predição baseada na entrada

Regressão Linear - função de custo

• A função de custo nos ajuda a guiar em como ajustar a melhor linha reta para nossos dados:
  • Encontrar os valores de $\theta_i$ (parâmetros)
  • Diferentes valores nos fornece diferentes funções
  • Se $\theta_0$ é $1.5$ e $\theta_1$ é 0, então temos uma linha reta paralela ao eixo $x$ ao longo de 1.5 em $y$
    Se $\theta_1 > 0$, então temos uma inclinação positiva

Regressão Linear - função de custo

• Baseado em nosso conjunto de treino, queremos gerar parâmetros que geram a linha reta

• Temos que escolher esses parâmetros tal que $h_\theta(x)$ é próxima a $y$ para nossos exemplos de treino.

• Basicamente, temos que usar os $x$'s do conjunto de treino em que $h_\theta(x)$ dá estimativas para $y$ o mais próximo possível

• Pense em $h_\theta(x)$ como um "imitador de $y$" - ele tenta converter the $x$ em $y$, considerando que já temos $y$ podemos avaliar como $h_\theta(x)$ se comporta

Regressão Linear - função de custo

• Para formalizar isso

• Queremos resolver um problema de minimização em minimizamos
  $(h_\theta(x) - y)^2$

• i.e., minimizar a diferença entre $h_\theta(x)$ e $y$ para cada um dos Exemplos

• Somar essa diferença em todo o conjunto de treino

$\frac{1}{2m} \sum_i^m (h_\theta(x) - y)^2$

Regressão Linear - função de custo

• Minimizar a diferença (ao quadrado) entre o valor predito e o valor real da casa
  • $\frac{1}{m}$ significa que calculamos a média
  • $\frac{1}{2m}$ o $2$ torna a matemática um pouco mais fácil, e nós não modificamos os valores dos parâmetros que obtemos (isto é, metado do valor mínimo ainda é o valor mínimo)
• Minimizar $\theta_0$ e $\theta_1$ significa que encontramos valores que, na média, produzem a menor diferença entre o valore real e o predito.

Regressão Linear - função de custo

• Mais precisamente, essa é uma função de custo

$J(\theta_0,\theta_1) = \frac{1}{2m} \sum_i^m (h_\theta(x) - y)^2$

• E queremos minimizar essa função de custo
  • Nossa função de custo está (por causa da somatória) inerentemente olhando TODOS os dados no conjunto de treino
• Essa função é também chamada de função de custo de erro quadrático
  • Provavelmente a função de custo mais usada

Regressão Linear - função de custo

Se fizermos um gráfico da função de custo em função de $\theta_0$ e $\theta_1$, teremos algo como

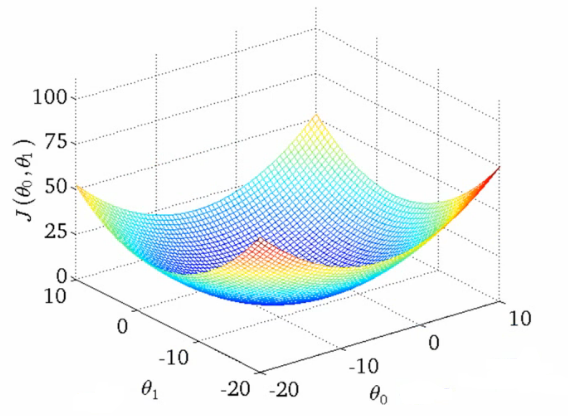
Regressão Linear - função de custo

Para simplificar, podemos refazer esse gráfico usando um gráfico de contornos

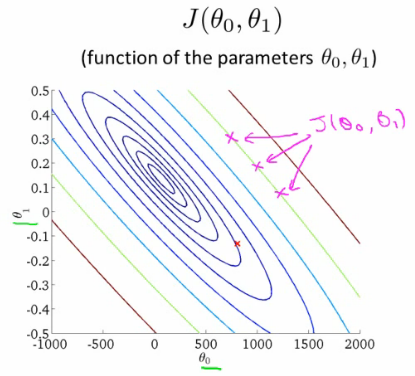
Algoritmo da descida do gradiente

• É usado para minimizar a função $J$
• É usado em vários algoritmos de machine learning para minimizar funções.

Algoritmo da descida do gradiente

• Inicie com um valor qualquer
  • inicie com 0,0 (ou um valor aleatório)
• Modifique os valores de $\theta_0$ e $\theta_1$ um pouco para tentar reduzir $J(\theta_0, \theta_1)$
• Cada vez que você reduzir os parâmetros, selecione o gradiente que reduz $J(\theta_0, \theta_1)$ o mais possível
• Repita o processo até que você convirga para um mínimo local
• Dependendo da função de custo, onde você inicia determina qual o mínimo você vai obter

Algoritmo da descida do gradiente

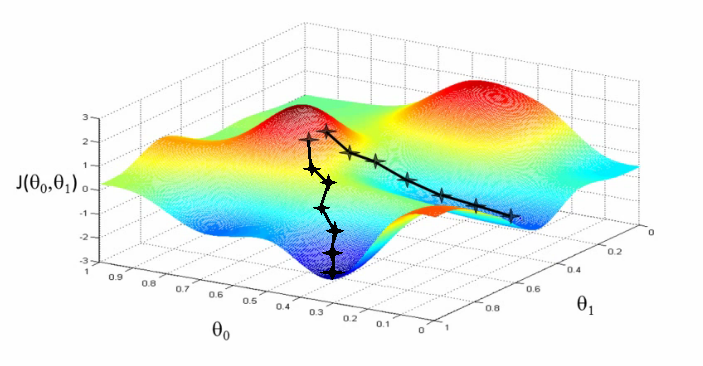
Algoritmo da descida do gradiente

• Mais formalmente, use a regra de atualização

$\theta_j := \theta_j - \alpha \frac{\partial}{\partial\theta_j} J(\theta_0, \theta_1)$

a cada iteração para $j \in \{0,1\}$ até convergir

• $\alpha$ é um número chamado de taxa de aprendizado
• Ele controla o "tamanho do passo"
  • Se $\alpha$ é grande, temos uma descida agressiva do gradiente
  • Se $\alpha$ é pequeno, dá passos pequenos

Algoritmo da descida do gradiente para regressão Linear

• Qual é o gradiente da nossa função de custo?
  $\frac{\partial}{\partial\theta_j} J(\theta_0,\theta_1) = \frac{\partial}{\partial\theta_j} \left( \frac{1}{2m} \sum_i^m (h_\theta(x^i) - y^i)^2 \right)$

• substituindo $h_\theta(x)$ por $\theta_0 + \theta_1 x$

$= \frac{\partial}{\partial\theta_j} \left( \frac{1}{2m} \sum_i^m (\theta_0 + \theta_1 x^i - y^i)^2 \right)$

Algoritmo da descida do gradiente para regressão Linear

• Agora derivando parcialmente:

$j = 0 : \frac{\partial}{\partial\theta_0} J(\theta_0,\theta_1) = \frac{1}{m} \sum_i^m (h_\theta(x^i) - y^i)$

$j = 1 : \frac{\partial}{\partial\theta_1} J(\theta_0,\theta_1) = \frac{1}{m} \sum_i^m (h_\theta(x^i) - y^i) x^i$

Algoritmo da descida do gradiente para regressão Linear

• Como a função de custo da regressão linear é convexa, ela tem um único mínimo
  • O método da descida do gradiente sempre encontrará o melhor valor de $\theta_0$ e $\theta_1$
  • Um único ótimo global

Algoritmo da descida do gradiente para regressão Linear

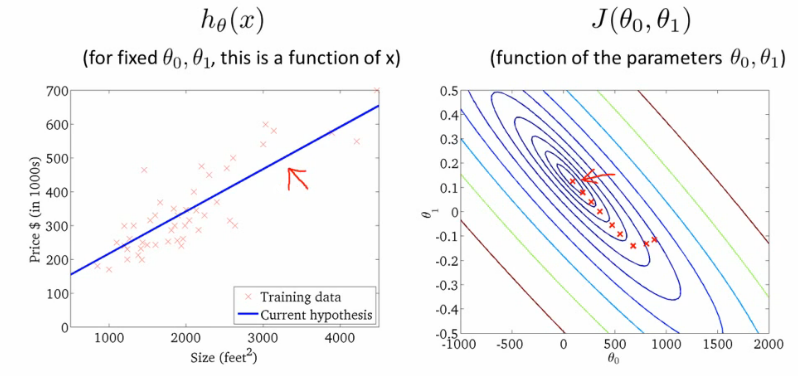
Algoritmo da descida do gradiente para regressão Linear

• Existe um algoritmo numérico para encontrar a solução que minimiza a função.
  • Método da Equação normal
  • O gradiente descendente é melhor para conjuntos de dados grandes
• Usado em vários contextos e em aprendizado de máquina