Aprendizado de Máquina

Redução de dimensionalidade

Prof. Ronaldo Cristiano Prati

ronaldo.prati@ufabc.edu.br

Bloco A, sala 513-2

Maldição da dimensionalidade

• A princípio, aumentar o número de atributos tem o potencial de melhorar o desempenho

• Na prática, em muitos casos, mais atributos podem levar a uma degração no desempenho

• Número de exemplos de treinamento necessário cresce exponencialmente com o número de dimensões

Maldição da dimensionalidade

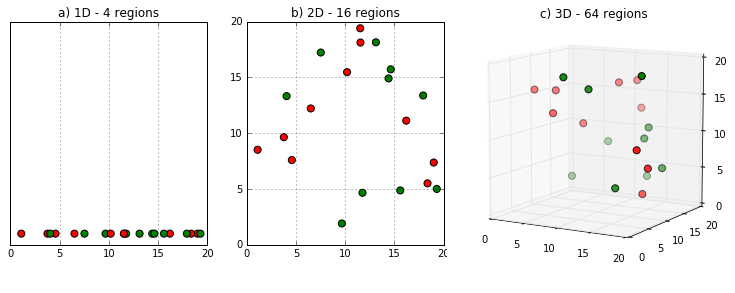
Redução da dimensionalidade

• Em muitos casos, podemos reduzir a dimensionalidade dos dados
  • Selecionar um subconjunto de atributos mais relevantes
  • Combinar atributos usando transformações (lineares ou não lineares)

Transformação de atributos

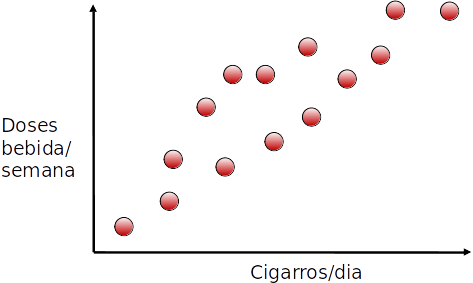
• Ambos atributos crescem juntos (estão correlacionados)
• Podemos combiná-los em um único atributo?

Transformação de atributos

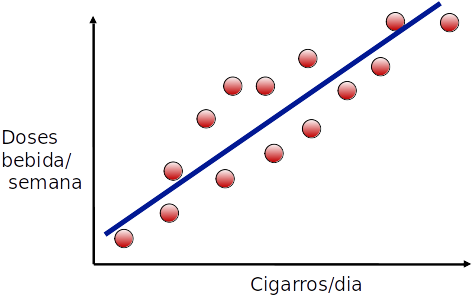
• Podemos encontrar a linha que minimiza a distância dos pontos à linha

Transformação de atributos

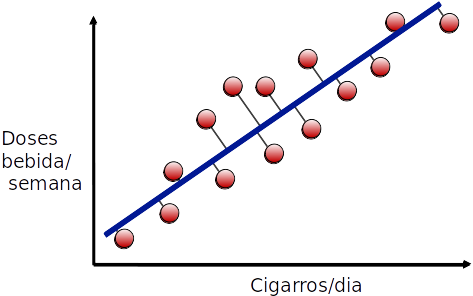
• E projetar os pontos nessa linha

Transformação de atributos

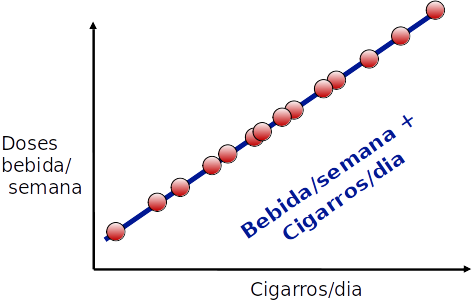
• Essa projeção é representada por um único atributo que faz uma combinação linear eentre bebida/semana e cigarros/dia

Transformação de atributos

• Esse é o princípio por trás da Análise de Componentes principais
• Dado um conjunto de dados com $n$ dimensões, encontrar uma projeção linear em $p$ dimensões, de maneira que $p<n$.
• Essa projeção deve minimizar a perda de informação.

PCA

• Dado um conjunto de dados $n$-dimensional, encontrar uma matriz $U$ de dimensões $n\times k$ tal que:
  • $z = U^\intercal x$, em que $z$ tem uma dimensão $k<n$.
  • Minimizar o erro de projeção
  • As novas variáveis de $z$ são linearmente não correlacionadas.

PCA

• Como encontrar a matriz $U$?
  • O vetor $u^1$ (primeira coluna de $U$) indica a direção de maior variância de $X$
  • O segundo vetor $u^2$ indica a próxima direção de maior variância, desconsiderando a primeira
  • E assim por diante

PCA

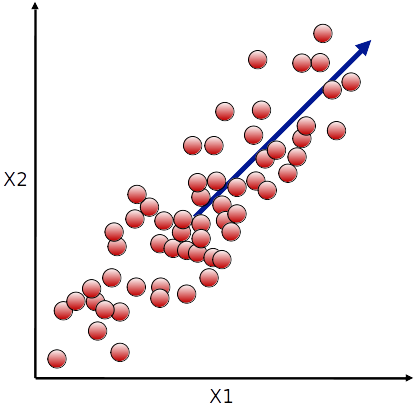
PCA

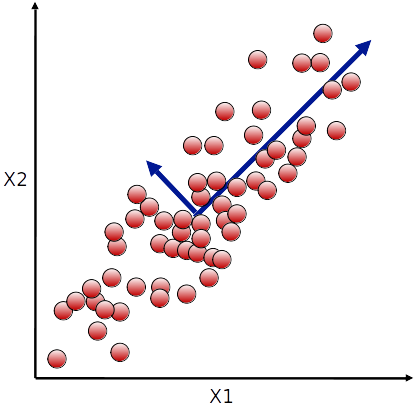
PCA

• Como encontrar a matriz $U$?
  • Centrar os dados (para cada atributo, subtrair a média)
  • Eventualmente colocar na mesma escala (dividir pela variância)
• Os vetores $u^i$ são os auto-vetores da matriz de correlação de x

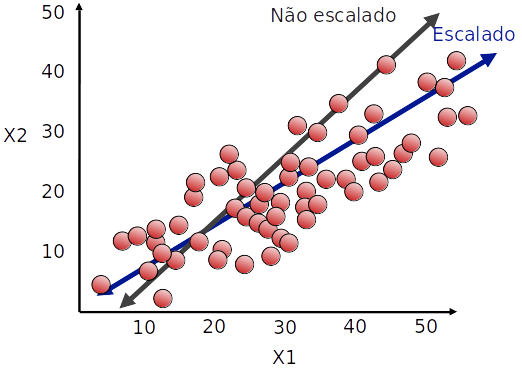
Ajuste de escala

• Variância é sensível a escala

Matriz de correlação

• Correlação de cada atributo com os demais

$XX^\intercal = \begin{bmatrix} \sigma(x_1,x_1), \sigma(x_1,x_2), \dots, \sigma(x_1,x_n)\\ \sigma(x_2,x_1), \sigma(x_2,x_2), \dots, \sigma(x_2,x_n)\\ \vdots \\ \sigma(x_n,x_1), \sigma(x_n,x_2), \dots, \sigma(x_n,x_n) \end{bmatrix}$

SVD

• Uma maneira de computar os auto-vetores de $M$ é usar decomposição em valores singulares (SVD)

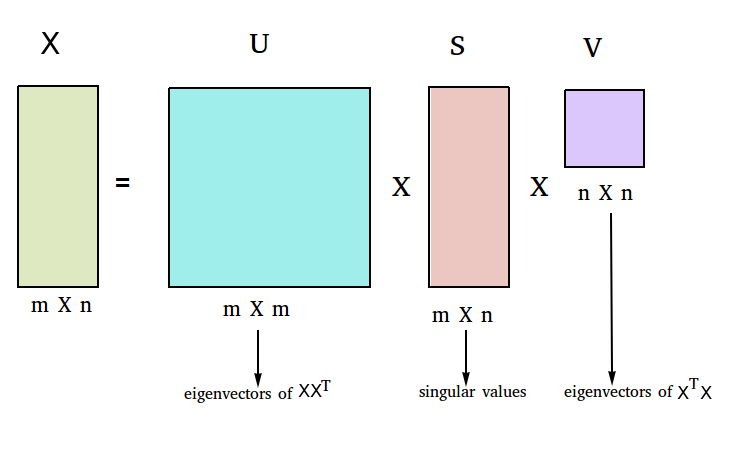
SVD e PCA

• Para fazer a redução de dimensionalidade, podemos usar a matriz $U_{reduzida}$, com as $k$ primeiras colunas de $U$
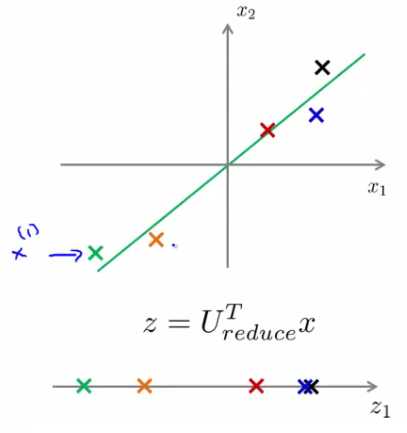
• Quando fazemos $(U_{reduzida})^\intercal x$, temos uma projeção de x em $k$ dimensões:
  • $z = (U_{reduzida})^\intercal x$ tem dimensão $k\times n$, e $X$ tem dimensão $n \times 1$, e obtemos a projeção de $x$ com dimensão $k\times 1$

Reconstrução

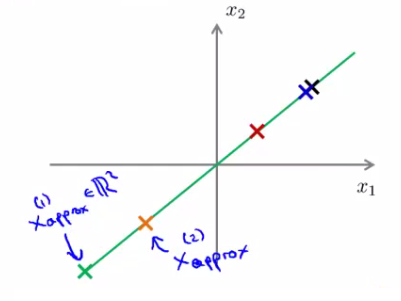
• Podemos "reconstruir" os dados para a dimensão original
  • Sair do espaço de dimensão $k$ e voltar para a dimensão $n$
• Para isso, fazemos $x_{aproximado} = (U_{reduzida}) z$
• Obviamente há uma perda de informação com relação à $x$

Reconstrução

Aplicação

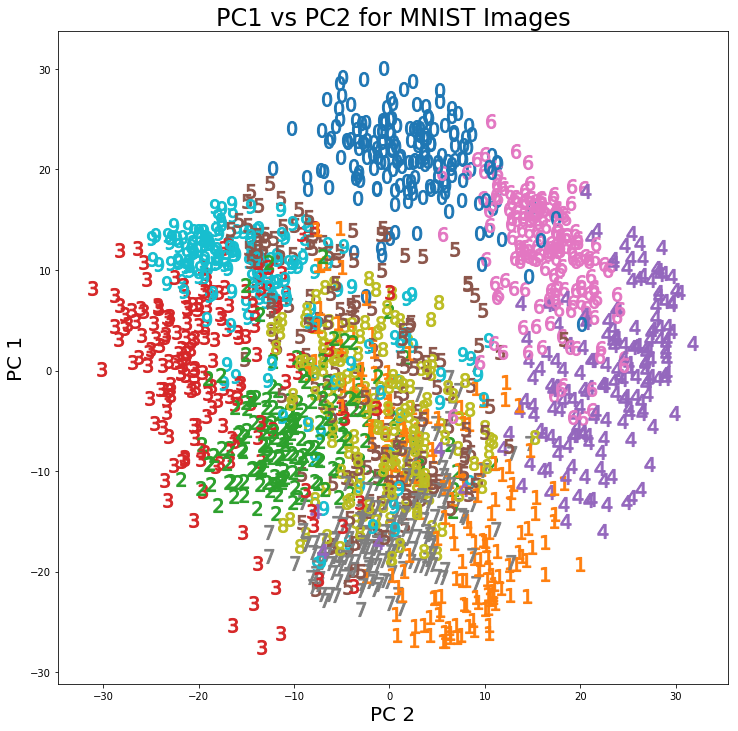
• Compressão de imagem

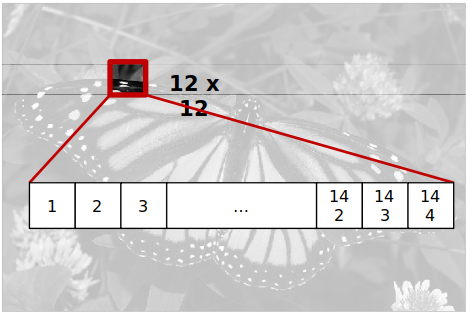
Aplicação

• Redução para 60 dimensões

Aplicação

• Redução para 16 dimensões

Aplicação

• 16 autovetores mais relevantes

Aplicação

• Redução para 4 dimensões

Aplicação

• 4 autovetores mais relevantes

Valor de $k$

• Uma estratégia para escolher o número de componentes principais é atribuir um valor mínimo $\epsilon$ para erro de projeção:

$\frac{\sum_i^m \|x - x_{aproximado}\|^2 }{\sum_i^m \|x\|^2} \leq \epsilon$

• Começamos com $k=1$, e vamos aumentando o número de dimensões até o erro de projeção seja menor que $\epsilon$

Kernel PCA

• As tranformações feitas pelo PCA são lineares
• Caso os atributos tenham correlação não linear, a projeção pode falhar
• Podemos usar a ideia de kernel (similar como fizemos com SVMs) para fazer projeções não lineares

Kernel PCA

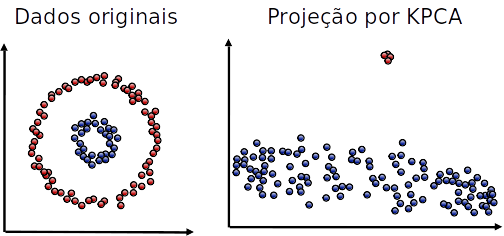
Kernel PCA

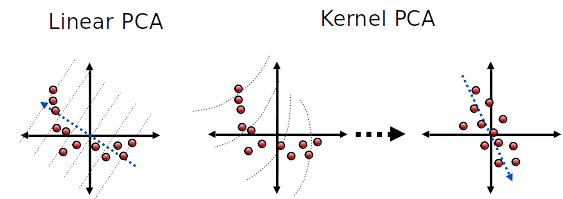
Outras abordagens não lineares

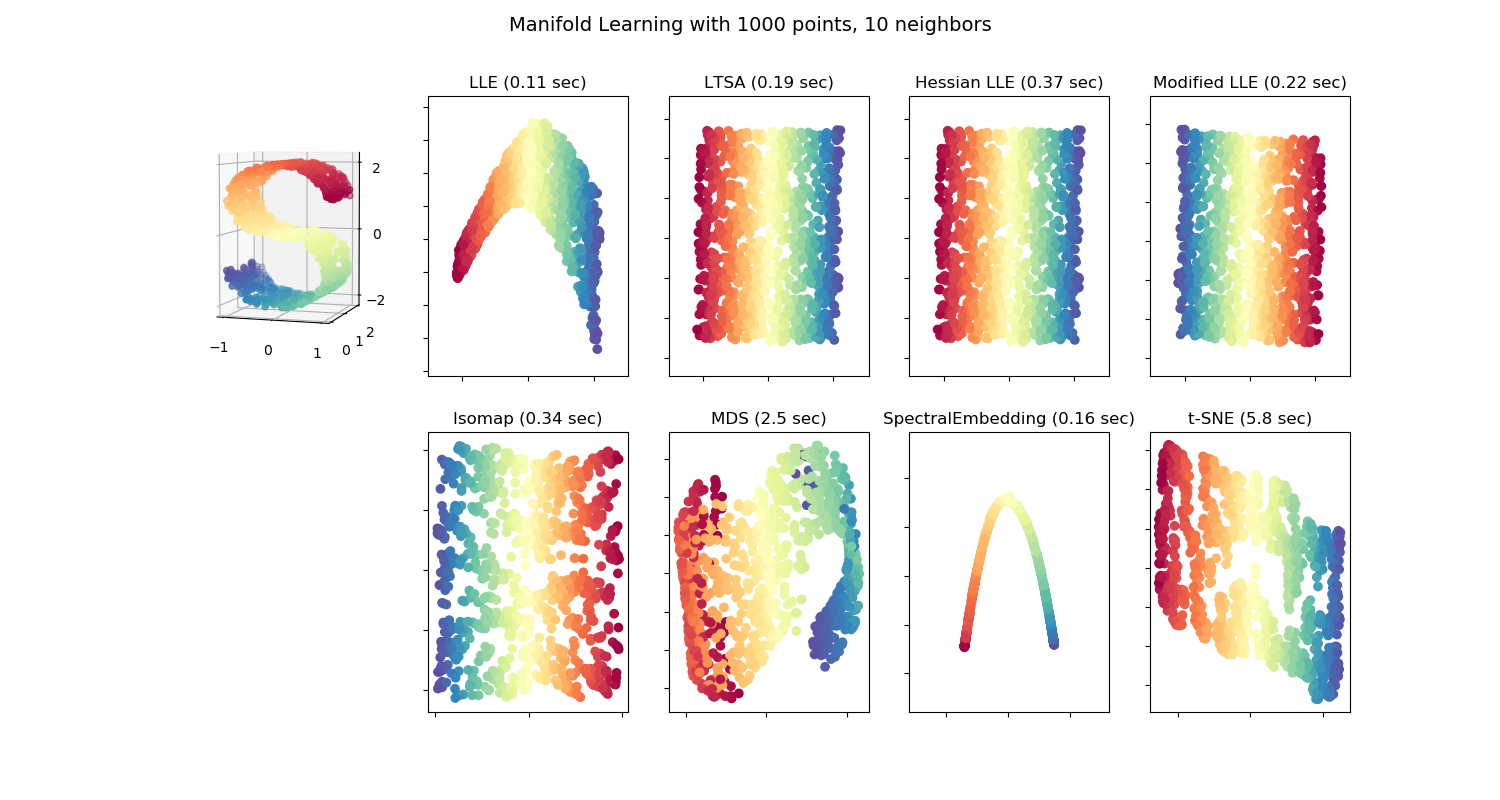
Seleção de Atributos

• Ao contrário da combinação de atributos, que combina todos atributos em um subconjunto menor, na seleção descartamos atributos para reduzir a dimensionalidade.
  • Atributos redundantes: se temos 2 atributos correlacionadas, podemos escolher apenas 1
  • Atributos irrelevantes: atributo pode não estar relacionado com a tarefa

Seleção de Atributos

• Muitos algoritmos de AM são projetados de modo a selecionar os atributos mais apropriados para a tomada de decisão
• Algoritmos de indução de árvores de decisão (falaremos um pouco mais a frente desses algoritmos) são projetados para:
  • Escolher o atributo mais promissor para particionar o conjunto de dados
  • Não selecionar atributos irrelevantes

Seleção de Atributos

• Devido à maldição da dimensionalidade, no entanto, a adição de atributos irrelevantes à base de dados, geralmente, "confunde" o algoritmo de aprendizado

• Simulações mostram uma degração média de 5 a 10% quando atributos irrelevantes são adicionados

Seleção de Atributos

• Seleção de atributos antes do aprendizado

  • Pode melhorar o desempenho preditivo
  • Acelera o processo de aprendizado

• Produz uma representação mais compacta do conceito a ser aprendido

  • O foco será nos atributos que realmente são importantes para a definição do conceito

Seleção de Atributos

• O processo de seleção de atributos, às vezes, pode ser muito mais custoso que o processo de aprendizado

• Ou seja, quando somarmos os custos das duas etapas, pode não haver vantagem

Métodos de Seleção de Atributos

• Manual

• Ideal se for baseado em um entendimento profundo sobre ambos:

  • O problema de aprendizado
  • O significado de cada atributo

• Entretanto, tende a ser bastante custoso.

Métodos de Seleção de Atributos

• Automático

• Filtros: método usado antes do processo de aprendizado para selecionar o subconjunto de atributos

• Wrappers: o processo de escolha do subconjunto de atributos está “empacotado” com o algoritmo de aprendizado sendo utilizado

Filtros

• O método de filtro geralmente é unidimensional (avalia cada atributo individualmente).
• Não consegue identificar atributos redundantes.
• Baseado em alguma medição sobre o atributo (correlação com o atributo meta, por exemplo).
• Os atributos cuja medida é maior que um limite (definido pelo usuário) são selecionados.

Seleção Multivariada

• Implica em uma busca no “espaço” de atributos.

• O número de possíveis combinaçõe de atributos é $O(2^m)$, em que $m$ é o número total de atributos.

• Portanto, na maioria dos casos práticos, uma busca exaustiva não é viável.

• Solução: busca heurística

Espaço de Busca

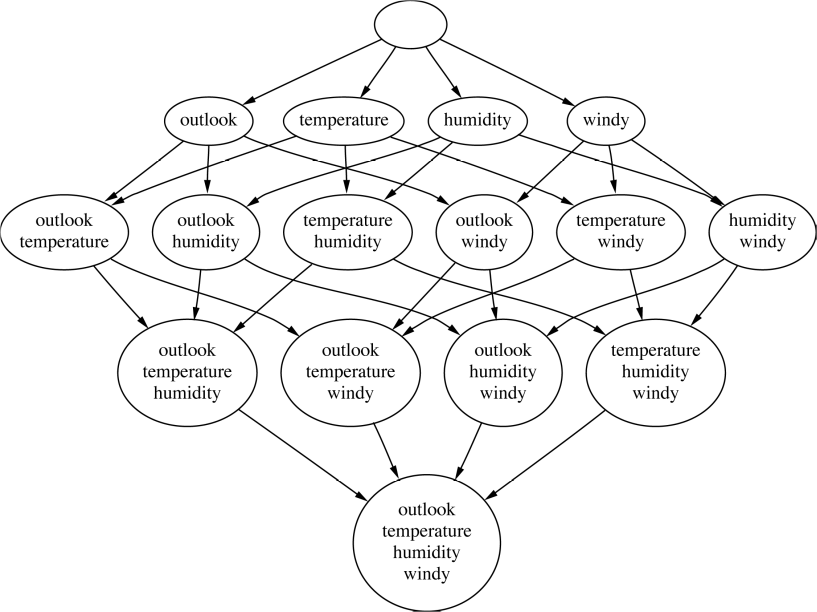
Busca Heurística no Espaço de Atributos

• Busca para Frente (Seleção Forward)

  • A busca é iniciada sem atributos e os mesmos são adicionados um a um
  • Cada atributo é adicionado isoladamente e o conjunto resultante é avaliado segundo um critério
  • O atributo que produz o melhor critério é incorporado

Busca Heurística no Espaço de Atributos

• Busca para trás (Eliminaçao Backward)

  • Similar a Seleção Forward

  • Começa com todo o conjunto de atributos, eliminando um atributo a cada passo

Busca Heurística no Espaço de Atributos

• Podemos usar a acurácia de um modelo como critério de avaliação (wrapper)

• Tanto na Seleção Forward quanto na Eliminação Backward , pode-se adicionar um peso por subconjuntos pequenos

• Por exemplo, pode-se requerer não apenas que a medida de avaliação crescer a cada passo, mas que ela cresça mais que uma determinada constante

Busca Heurística no Espaço de Atributos

• Outros métodos de busca:
  • Busca bidirecional
  • Best-first search
  • Beam search
  • Algoritmos genéticos