Aprendizado de Máquina

Combinando modelos

Prof. Ronaldo Cristiano Prati

ronaldo.prati@ufabc.edu.br

Bloco A, sala 513-2

Por que combinar modelos?

• Quando precisamos decidir sobre uma questão critica, usualmente consultamos vários experts da área ao invés de confiarem no julgamento de um único consultor

• Em aprendizado de máquina, um modelo pode ser considerado como um “expert”. Então combina-los é uma boa idéia?

Vantagens

• Experimentalmente tem sido mostrado que modelos combinados apresentam melhores desempenhos do que um sistema decisório único

• Melhor do que o melhor modelo selecionado usando cross validation.

• Neutraliza ou minimiza drasticamente a instabilidade inerente dos algoritmos de aprendizagem.

Vantagens

• Sistemas combinados reduzem a variância (decomposição bias-variance)

• Em geral, quanto maior for o número de classificadores combinados, maior a redução da variância

Desvantagens

• Apesar de normalmente os sistemas combinados apresentarem melhores resultados, não há garantias que isto ocorrerá sempre.

• Ainda é uma área de pesquisa com muito pontos para serem confirmados teoricamente.

• Modelos combinados são mais difíceis de analisar.

• Custo computacional

Como combinar?

• Três aspectos a serem analisados na combinação de modelos
  • A escolha da estrutura do sistema
  • A escolha dos componentes do sistema
  • A escolha do método de combinação

Como combinar?

• A estrutura do sistema

  • A maneira como os componentes estão organizados dentro do sistema
    -Quantos métodos serão necessários e como organizá-los?

• Tipos:

  • Ensemble
  • Modular

Ensembles

• Também conhecido por vários outros nomes:

  • Multiple classifier systems, committee of classifiers, ou mixture of experts.

• Tem sido utilizado com sucesso em problemas onde um único modelo não funciona bem.

• Bons resultados são encontrados em várias aplicações em uma larga variedade de cenários

Comitês

• Abordagem: redudante ou paralela de combinação

• Modelos: treinados com a mesma tarefa

• Suas respostas são combinadas para produzir estimativas mais confiáveis

Ensembles

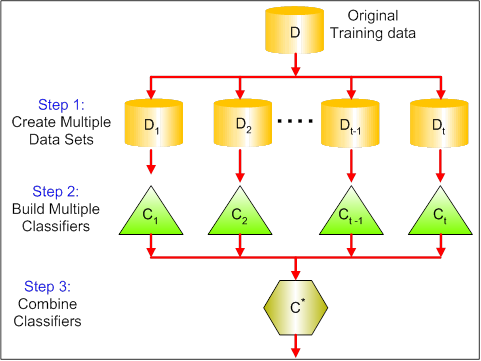
Dividir e Conquistar

• Independente da quantidade de dados alguns problemas são muito difíceis de serem resolvidos por um dado classificador

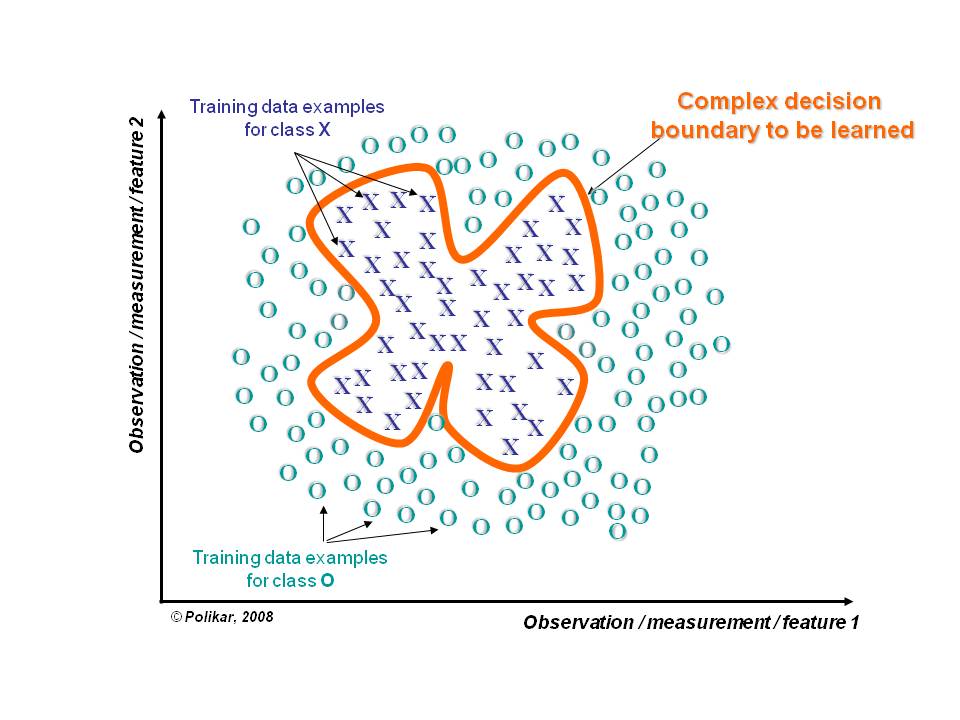
Dividir e Conquistar

A fronteira de decisão que separa os dados de diferentes classes pode ser muito complexa ou estar fora do escopo do classificador.

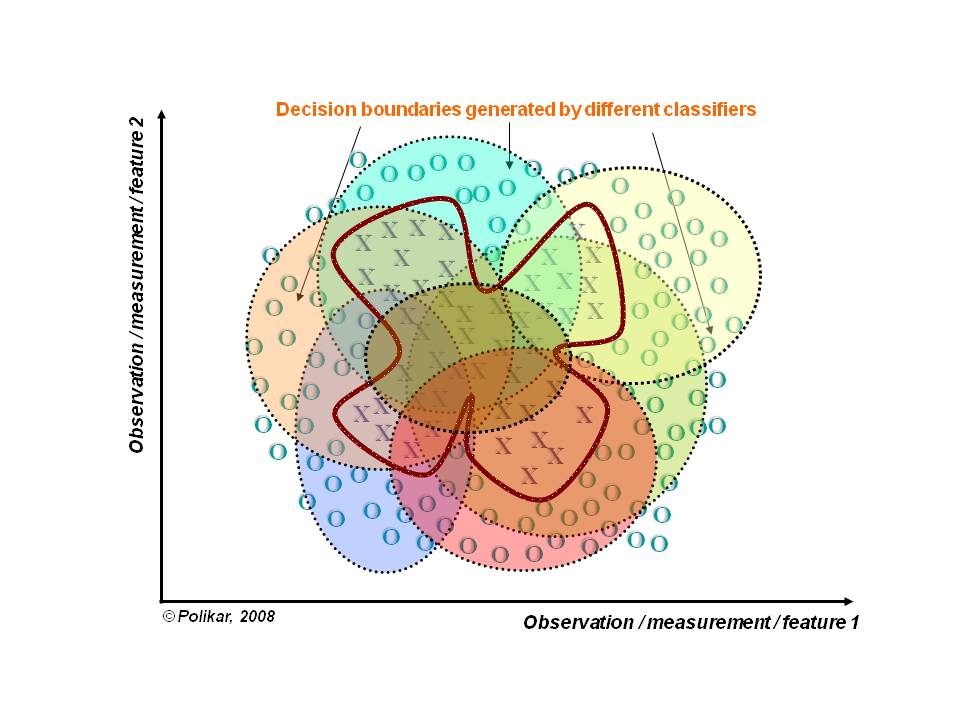
Dividir e Conquistar

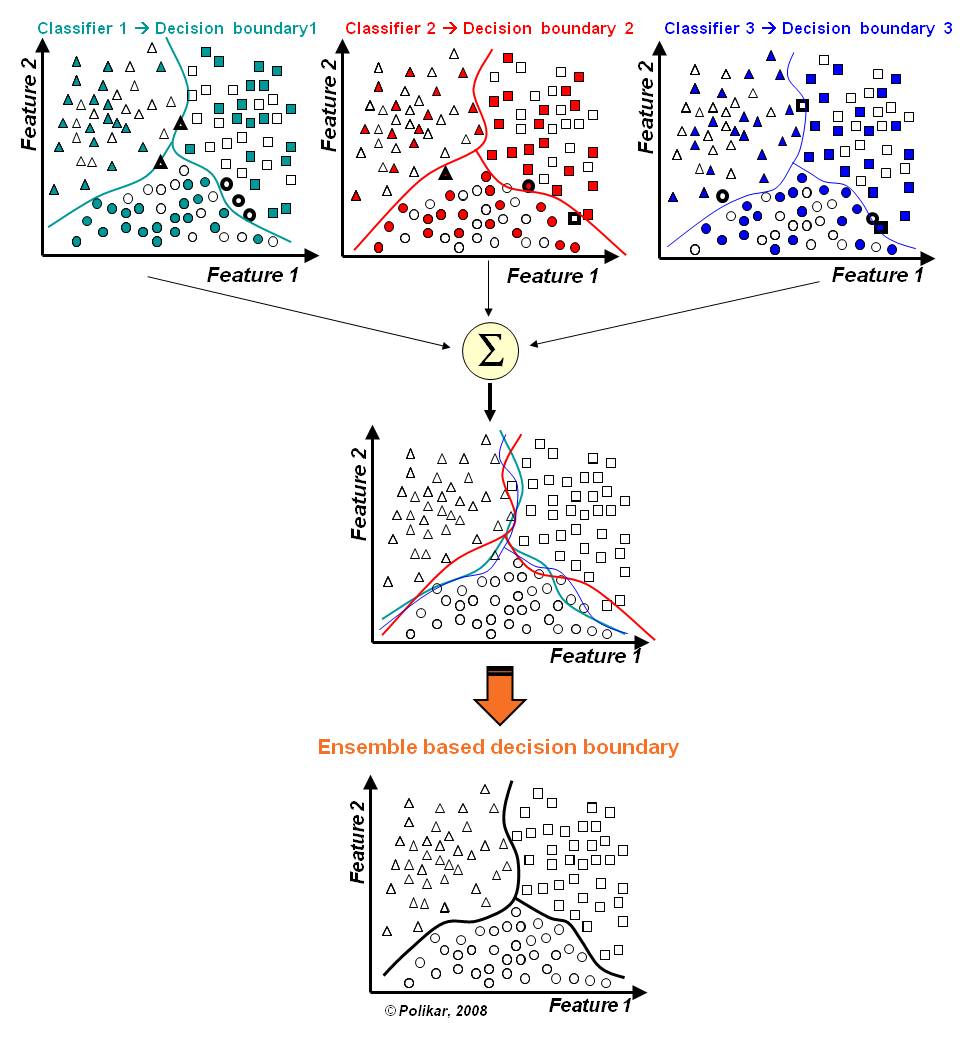
• A idéia de ensembles é que o sistema de classificação siga a abordagem dividir-para-conquistar;

• O espaço de dados é dividido em porções menores e mais “fáceis” de aprender por diferentes classificadores;

• Assim a linha base da fronteira de decisão pode ser aproximada por meio de uma combinação apropriada dos diferentes classificadores.

Dividir e Conquistar

Classificadores "fracos"

• Muitos ensembles usam modelos "fracos" (weak classifier)

  • Hipóteses simples, de rápido treinamento, e que tem um desempenho um pouco superior a uma predição Aleatóriedade
  • Pequeno bias, alta variância.

• A combinação das saídas produzidas pelos classificadores reduz o risco de escolha por um classificador com um pobre desempenho

Ensembles

• Os modelos são componentes que fornecem redundância

  • Uma solução para o mesmo problema, mesmo que usando meios diferentes

• Um aspecto importante é diversidade

  • Não há nenhuma vantagem em um ensemble com métodos idênticos

Diversidade

• O sucesso de um ensemble e a habilidade em corrigir erros de alguns de seus membros, depende fortemente da diversidade dos classificadores que o compõem;
• Cada classificador DEVE ter diferentes erros em diferentes exemplos dos dados;
• A idéia é construir muitos models e então combinar suas saídas de modo que o desempenho final seja melhor do que o desempenho de um único classificador;

Diversidade

• A diversidade de classificadores pode ser obtida de diferentes formas:

1. Nos dados
2. Nos modelos
3. Nas técnicas de modelagem
4. Na aleatoriedade

Diversidade

• Dados:
  • usar amostras diferentes (por exemplo, gerar diferentes amostras com reposição)
  • usar conjuntos de atributos diferentes (selecionar alatóriamente subconjuntos de atributos)

Diversidade

• Modelos:
  • usar parâmetros diferentes (diferentes valores de regularização, camadas em redes neurais, etc.)
  • atribuir pesos diferentes a a modelos

Diversidade

• Técnicas de modelagem:
  • Usar algoritmos diferentes
  • usar kernels diferentes para uma mesma dase de Dados

Diversidade

• Aleatóriedade
  • Usar pesos diferentes em nas inicializações
  • Decidir empates aleatóreamente

Ensembles também são úteis:

• Grandes volumes de dados
  • A quantidade de dados é grande para ser manipulada por um único classificador.
  • Particionar os dados em sub-conjuntos e treinar diferentes classificadores com diferentes partições dos dados e então combinar as saídas com uma inteligente regra de combinação.

Ensembles também são úteis:

• Pequenos volumes de dados
  • Quando há ausência de dados de treinamento técnicas de amostragem podem ser utilizadas para a criação de subconjuntos de dados aleatórios sobrepostos
  • Cada subconjunto é utilizado para treinar diferentes classificadores e então criar ensembles com desempenhos melhores a modelos com a base reduzida.

Técnicas de Criação de Ensembles

• As técnicas mais conhecidas que combinam modelos para problemas de regressão e classificação são:

  • BAGGING

  • BOOSTING

Bagging

• Possui uma implementação simples e intuitiva;

• A diversidade é obtida com o uso de diferentes subconjuntos de dados aleatoriamente criados com reposição;

• Cada subconjunto é usado para treinar um classificador do mesmo tipo;

• As saídas dos classificadores são combinadas por meio do voto majoritário com base em suas decisões;

Exemplo: Random Forests

• Usado para a construção de ensembles com árvores de decisão;

• Variação da quantidade de dados e atributos;

• Usando árvores de decisão com diferentes inicializações;

Árvore de Decisão

• Divide recursivamente o espaço de exemplos:
  1. Escolhe um atributo
  2. Particiona os dados de acordo com esse atributo
  3. Para cada subconjunto gerado, repete volta ao passo 1 até que o subconjunto seja homogêneo

Árvore de Decisão

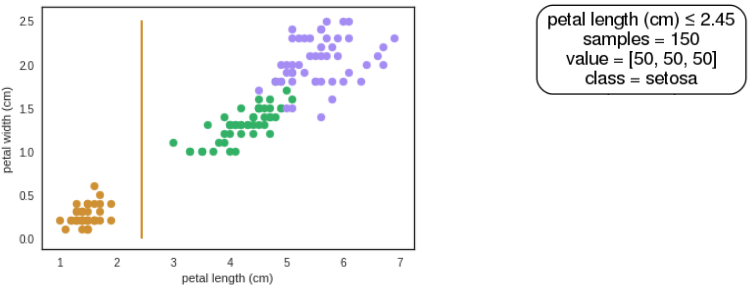
Árvore de Decisão

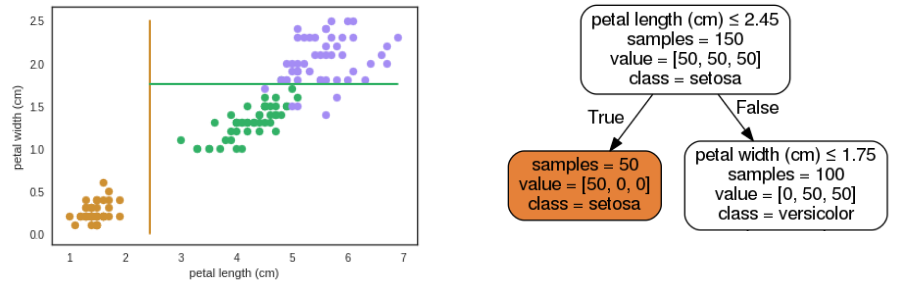
Árvore de Decisão

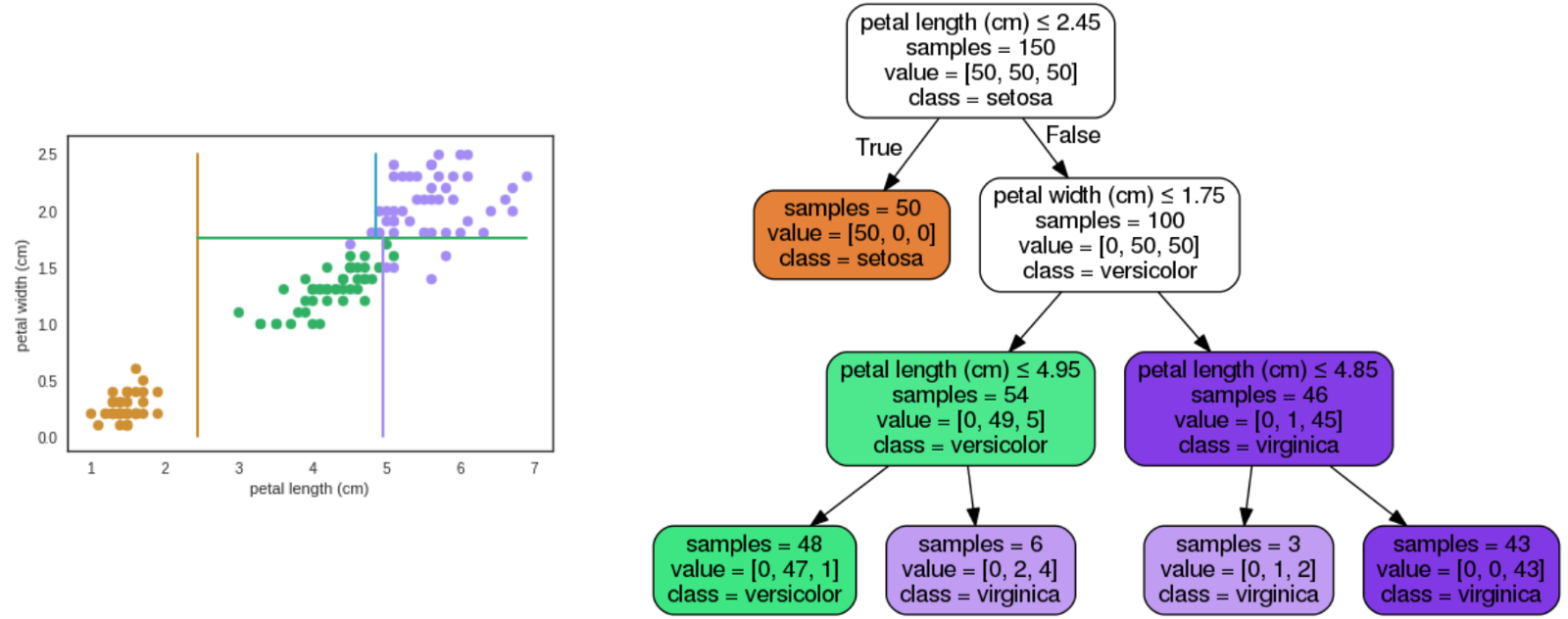
Exemplo: Random Forests

• Por que usar uma floresta?
  • Uma única árvore complexa requer muitos exemplos
  • Como a escolha do atributo é heurística, um escolha ruim compromote toda a sub-árvore
  • Uma combinação de várias árvores simples pode gerar uma froteira de decisão complexa

Random Forests

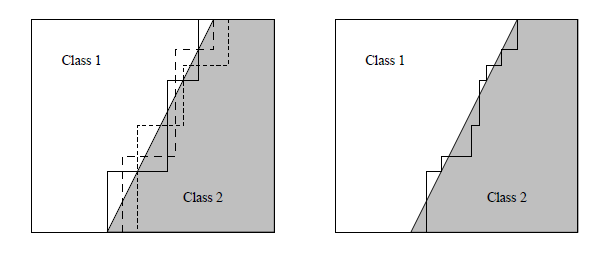
BOOSTING

• Focar em exemplos mais "difíceis" de classificar
• Cria um modelo inicial, e marca os exemplos em que o modelo tem um desempenho ruim
• Iterativamente cria um novo novo modelo, atribuindo um custo maior ao exemplos incorretos na interação anterior
• Atribui um peso diferente e decrescente (para evitar overfitting) a cada modelo

BOOSTING

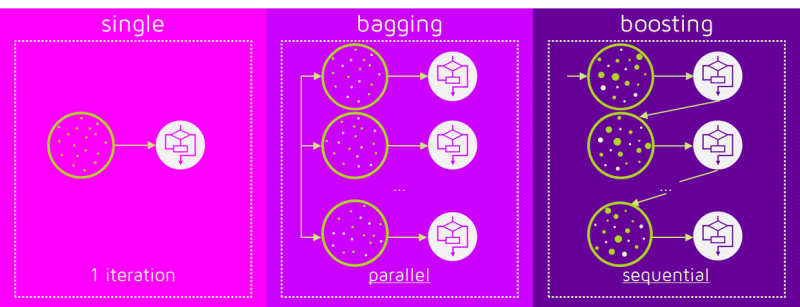
Exemplo: Gradient Boosting

1. Treinar um modelo simples
2. Calcular o residual (diferença entre valor predito e o real)
3. Cria um novo modelo usando o resíduo como atributo alvo
4. Adiciona o residual predito em 3. ao valor predito em 1
5. Repetir os passos 1 a 5 até convergir

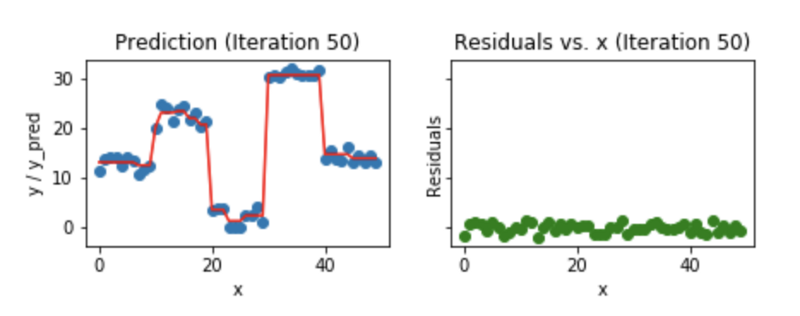
Exemplo: Gradient Boosting

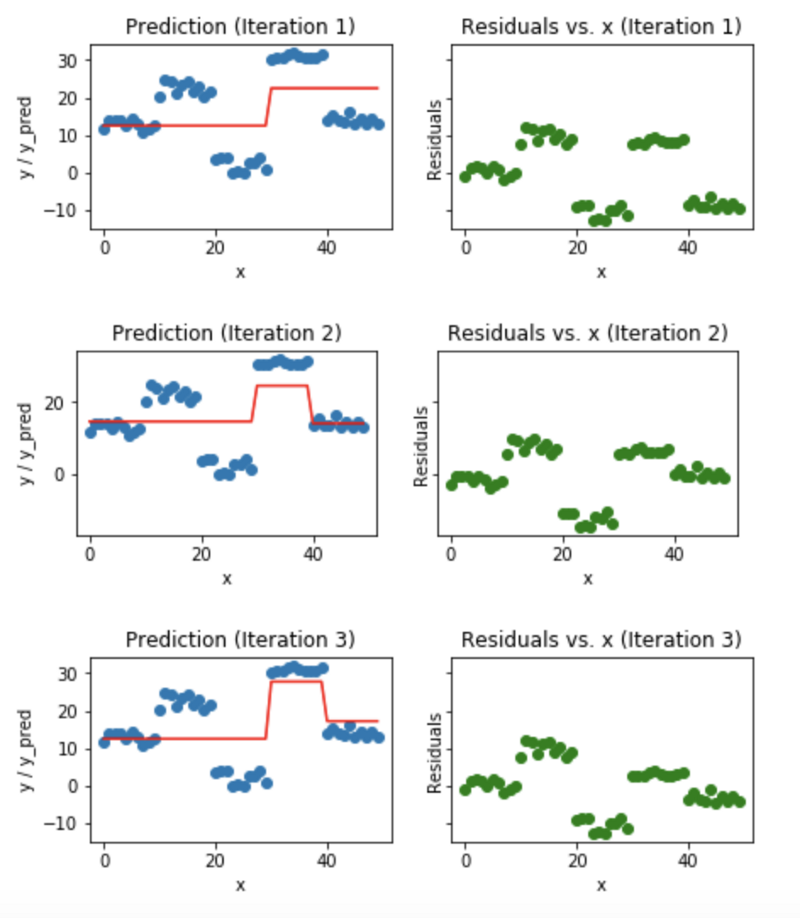
Exemplo: Gradient Boosting

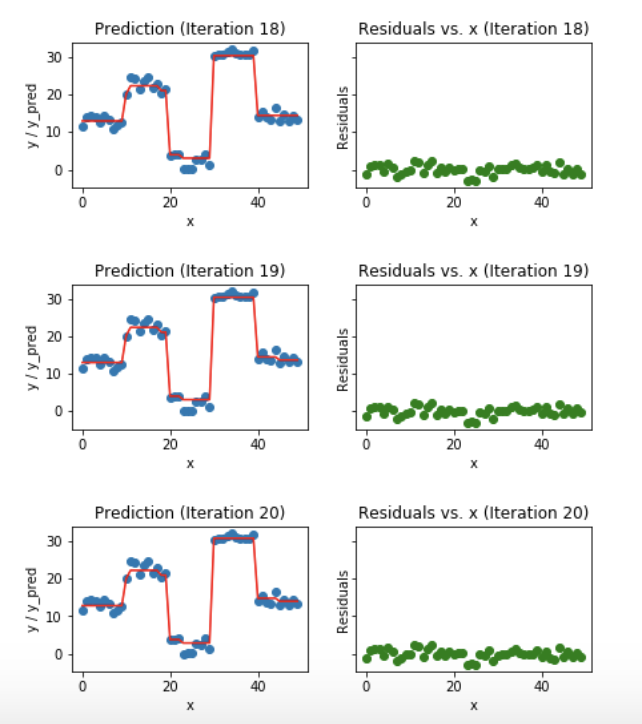
Exemplo: Gradient Boosting

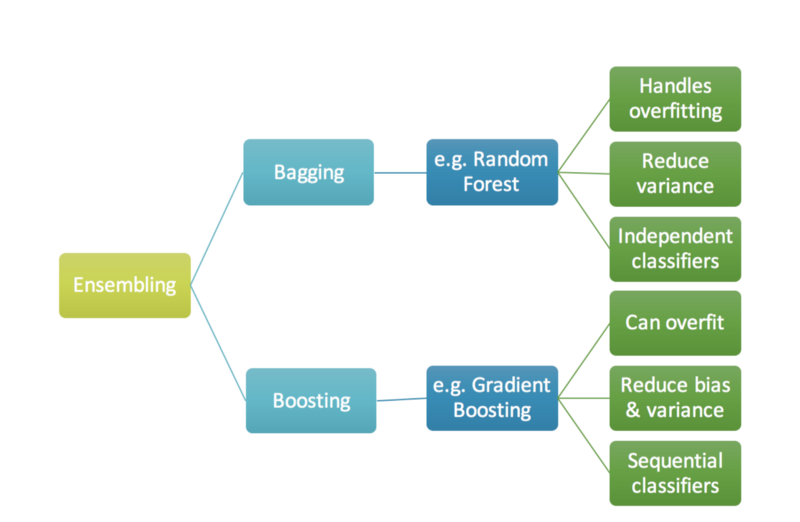
Bagging versus boosting

• A combinação de modelos do bagging pode reduzir overfitting. Ele atua principalmente na componente de variância do erro, e pode ser executado em paralelo.

• Já o boosting pode atuar tanto na componente de bias quando na de variância do erro. Entretanto, ele pode levar a um overfitting e é executado sequencialmente.

Bagging versus boosting