Aprendizado de Máquina
Prof. Ronaldo Cristiano Prati
ronaldo.prati@ufabc.edu.br
Bloco A, Sala 513-2
Tópicos da Aula
- Implementações do algoritmo da descida do gradiente para regressão linear
- Direta
- Vetorizada (
numpy) - Algebra Linear
- Regressão linear multivariada
Função de custo
- Vamos definir a função de custo (em python). As variáveis
xeysão listas de tamanho m, ethetaé uma lista de tamanho 2.
def costFunction(x,y,theta): error = 0 m = len(x) for i in range(m): error += ((theta[0] + theta[1]*x[i]) - y[i])**2 return error / (2*m)
Descida do Gradiente (1 passo)
- Calcula o gradiente em cada ponto e calcula o novo valor de θ.
def step_gradient(x,y,theta,alpha): new_theta = [0,0] m = len(x) theta_0_grad = [] theta_1_grad = [] for i in range(m): theta_0_grad.append((theta[0] + theta[1]*x[i]) - y[i]) theta_1_grad.append(((theta[0] + theta[1]*x[i]) - y[i])* x[i]) new_theta[0] = theta[0] - (alpha * sum(theta_0_grad)/m) new_theta[1] = theta[1] - (alpha * sum(theta_1_grad)/m) return(new_theta)
Descida do Gradiente (iterando)
- Chama o método
step_gradientiterativamente para atualizar o valor de θ. Armazena os valores intermediários para plotar
theta = [0,0] theta_logs = [theta] # para plotar cost_logs = [costFunction(x,y,theta)] # para plotar n_iter=200 alpha = 0.001 for i in range(n_iter): theta = step_gradient(x,y,theta,alpha) theta_logs.append(theta) # para plotar cost_logs.append(costFunction(x,y,theta)) # para plotar
Alpha = 0.03
Alpha = 0.02
Alpha = 0.01
Alpha = 0.001
Alpha = 0.0001
Vetorização
-
Algumas linguagens (como
matlabeR) permite o uso de técnicas de vetorização. Nessas linguagens, algumas operacoes são transparentemente aplicadas a vetores ou matrizes. -
Em
python, a bibliotecanumpyprovê várias funcionalidades para explorar vetorização
Função de custo - vetorizada
-
Uma versão da função de custo vetorizada é mostrada a seguir. Observe que não é utilizado o laço.
-
As variáveis
x,yethetadevem sernumpy.array
import numpy as np def costFunction(x,y,theta): error = np.sum(((theta[0] + theta[1]*x) - y)**2) return error / (2*m)
Descida do Gradiente (1 passo)
def step_gradient(x,y,theta,alpha): theta_gradient = np.zeros(2) theta_gradient[0] = np.mean((theta[0] + theta[1]*x) - y) theta_gradient[1] = np.mean(((theta[0] + theta[1]*x) - y)*x) new_theta = theta - (alpha * theta_gradient) return(new_theta)
Algebra linear
- Suponha que nosso modelo seja
hθ(x)=−40+0.25x
- Queremos aplicá-la em uma base de dados com 4 casas
| Tamanho |
|---|
| 2104 |
| 1416 |
| 1534 |
| 852 |
Algebra linear
- Podemos calcular o valor predito pelo modelo acrescentando uma coluna de 1's ao conjunto de dados, e multiplicando pela "matriz" de coeficientes.
⎣⎢⎢⎡1111210414161534852⎦⎥⎥⎤×[−400.25]=⎣⎢⎢⎡486.0314.0343.5173.0⎦⎥⎥⎤
- Isso pode ser muito mais eficiente computacionalmente que usar laços, e também facilita a codificação (se tivermos uma biblioteca de algegra linear)
Gradiente descendente - AlgLin
- Podemos reescrever a função de custo como:
Jθ(x)=2m1∑(xθ−y)2 - e o seu gradiente como:
∂θ∂Jθ(x)=m1((xθ−y)⊺x)⊺=m1(x⊺×(xθ−y)) - Para derivação do gradiente, veja aqui
Gradiente descendente - AlgLin
def costFunction(X, y, theta): error = np.dot(X, theta) - y return np.mean(error) / 2 def step_gradient(x,y,theta,alpha): m = len(x) theta = theta - (alpha/m) * np.dot(x.T, np.dot(x, theta) - y) return(theta) x = np.column_stack((np.ones(len(x)),x)) theta = [0,0] n_iter=200 alpha = 0.001 for i in range(n_iter): theta = step_gradient(x,y,theta,alpha)
Regressão linear multivariada
- Múltiplas variáveis = múltiplos atributos
- No problema anterior, tinhamos
- x = tamanho da casa (em ft2)
- y = preço da casa
- Mas podemos adicionar novas variáveis, tais como
- x1,x2,x3,x4 são quatro atributos:
x1 = tamanho (ft2)
x2 = número de quartos
x3 = number de andares
x4 = idade da casa (anos)
y = preço das casas
- x1,x2,x3,x4 são quatro atributos:
Mais notação
- n = número de atributos (n=4)
- m = número de exemplos
- xi = vetor de entrada para um exemplo. i é o índice do conjunto de treinamento, então x3 é, por exemplo a 3a casa. x é um vetor n-dimensional
- xji é o valor do atributo j do i-ésimo exemplo de treino. Por exemplo, x23 é o número de quartos da terceira casa.
Forma da hipótese
-
Anteriormente nossa hipótese era da forma:
hθ(x)=θ0+θ1x -
Agora que temos multiplos atributos:
hθ(x)=θ0+θ1x+θ2x+θ3x+θ4x -
Se adicionarmos uma feature adicional x0=1, em notação vetorial temos:
hθ(x)=θx
Descida do Gradiente
-
Os parâmetros ainda podem ser determinados pela função de custo
-
Atualizamos cada parâmetro θj fazendo
θj:=θj−α∂θj∂J(θ) -
em que
∂θj∂J(θ)=m1i∑m(hθ(xi)−yi)xji -
A forma vetorial se ajusta ao número de variáveis
Diferença de escala
- Atributos em diferentes escalas podem atrapalhar a descida do Gradiente. Por exemplo, se tivermos
x1 = Tamanho (0 - 2000 ft2)
x2 = número de quartos (1-5)
Os contornos gerados pelo plot de θ1 \emph{vs} θ2 será alongado em um dos eixos e estreito no outro
Diferença de escala
- Colocar os atributos na mesma escala pode fazer o algoritmo covergir mais rapidamente
- As linhas de contorno se parecerão mais com um círculo
- Possíveis opções
- Ajustar entre 0 e 1: max(xj)−min(xj)xji−min(xj)
- Normalização: σ(xj)xji−μ(xj)
Criação de atributos
- Suponha que tenhamos os atributos:
- x1 = Largura da frente to terreno
- x2 = Profundidade do terreno
- Podemos criar um novo atributo x3 = Área fazendo
x3=x1∗x2 - Em muitos casos, a definição de novos atributos pode gerar modelos melhores!
Regressão Polinomial
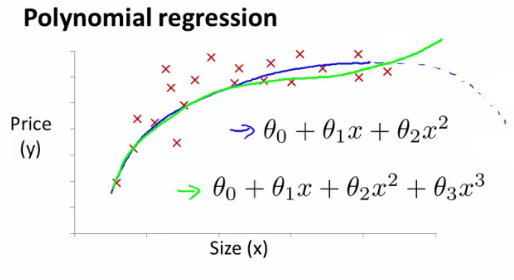
Regressão Polinomial
- Como podemos ajustar um polinômio de grau n>1 aos dados?
- Uma ideia simples é criar novos atribtos:
x1x2x3=x=x2=x3
- Criarndo atributos como esses e aplicando o algoritmo de regressão linear podemos fazer regressão polinomial!
Regressão Polinomial
- Reescalar os atributos se torna ainda mais importated nesse caso
- Ao invés de um polinômio convencional, também podemos usar xz1,z∈{2,3,…} (i.e., raiz quadrada, raiz cúbica, etc)
- Podemos criar muitos atributos - posteriormente vamos ver algoritmos para selecionar os melhores atributos
Equação normal
- Para alguns problemas de regressão linear, a equação normal provê uma melhor solução
- Até agora estivemos usando a descida do Gradiente
- Algoritmo iterativo que dá passos até convergir
- A equação normal resolve θ analiticamente
- Resolve para o valor ótimo de θ em um único passo
- Tem vantagens e desvantagens
Equação normal
- Vamos reescrever a função de custo Como
Jθ(x)=2m1(xθ−y)⊺(xθ−y)=2m1((xθ)⊺−y⊺)(xθ−y)=2m1(xθ)⊺(xθ)−(xθ)⊺y−y⊺(xθ)+y⊺y=2m1θ⊺x⊺xθ−2(xθ)⊺+y⊺y
Equação normal
- Calculando a derivada
∂θ∂J=2x⊺xθ−2x⊺y
- Igualando a zero (para achar o mínimo)
2x⊺xθ−2x⊺y2x⊺xθθ=0=2x⊺y=(x⊺x)−1x⊺y
Quando usar?
- Gradiente descendente:
- Precisa escolher a taxa de aprendizado
- Precisa de muitas iterações - pode ser demorado
- Funciona bem quando n é grande (adequado para Big Data)
Quando usar?
- Equação Normaliza
- não precisa escolher a taxa de aprendizado
- não precida iterar, checar convergencia, etc.
- Precisa inverter a matriz x⊺x (inverso de uma matrix n×n)
- Devagar se n é grande (pode ser bem lento)