---
presentation:
theme: beige.css
slideNumber: true
width: 1024
height: 768
---
## Aprendizado de Máquina
##### Prof. Ronaldo Cristiano Prati
[ronaldo.prati@ufabc.edu.br](mailto:ronaldo.prati@ufabc.edu.br)
###### Bloco A, Sala 513-2
### Classificação
- Um outro problema dentro de aprendizado supervisionado é a **classificação**
- $y$ é discreto:
- e-mail: SPAM/não SPAM?
- transções online: fraudulenta/normal?
- tumor: maligno/benigno?
- vamos começar com um problema de **classificação binária** (veremos multiclasse depois)
### Classificação
- Podemos usar regressão linear?
- $y$ pode ser representado como $0$ ou $1$:
- $0$: classe negativa
- $1$: classe positiva
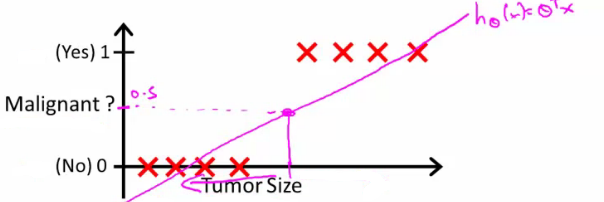
- Um ponto de corte no valor predito (p.ex. acima de 0.5), é classificado como classe positiva
### Classificação
- E se tivermos poucos exemplos da classe 1? Provavelmente a inclinação da reta seria menor, e classificaríamos tudo com classe $0$.
- Nossa hipótese também prediz valores abaixo de 0 e acima de 1, apesar da classe só poder assumir os valores 0 e 1.
- **Regressão logística** pode contornar esses problemas
### Regressão logística
- Apesar de se chamar regressão, é um algoritmo de classificação
- A hipótese tem a forma de $h_theta(x) = g((\theta^\intercal x))$, em que:
$$g(z) = \frac{1}{1+e^{-z}} $$
- Essa é a [**função sigmoid**](https://pt.wikipedia.org/wiki/Função_sigmóide) ou [**função logística**](https://pt.wikipedia.org/wiki/Função_sigmóide)
- Podemos reescrever $h_theta(x)$ como
$$h_\theta(z) = \frac{1}{1+e^{-\theta^\intercal x}} $$
### Regressão logística
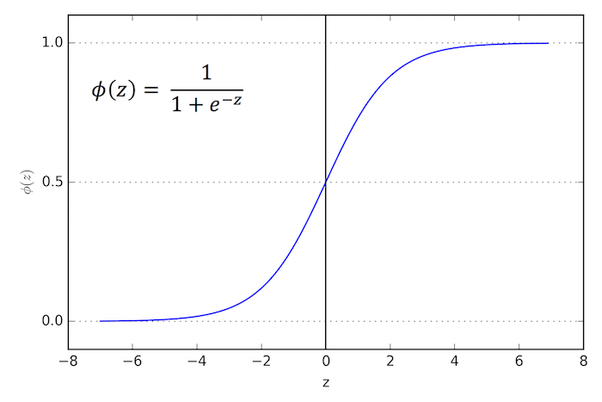
### Interpretando a saída
- A hipótese $h_\theta(x)$ dá como saída um número entre $0$ e $1$ que pode ser interpretada como a probabilidade que $y=1$ para a entrada $x$
- Por exemplo, se $h_\theta(x)=0.7$ para um certo $x^i$, o modelo dá $70\%$ de chance de um tumor malígno
- Em outras palavras, $h_\theta(x) = P(y=1|x,\theta)$
- Como o problema é binário, temos que:
$$
\begin{aligned}
P(y=1|x,\theta) + P(y=0|x,\theta) = 1\\
P(y=0|x,\theta) = 1 - P(y=1|x,\theta)
\end{aligned}
$$
### Fronteira de decisão
- Para predizer a classe, utilizamos aquela com maior probabilidade, segundo o modelo
- Isso é equivalente a predizer a classe $1$ se $h_\theta(x) > 0.5$, e a classe $0$ caso contrário
- Observando a função logística, temos que $h_\theta(x) = 0.5$ quando $z=0$.
- Como $z = \theta^\intercal x$, a linha $\theta^\intercal x = 0$ é a fronteira de decisão entre as duas classes
$\theta^\intercal x > 0$: predizer classe $1$
$\theta^\intercal x leq 0$: predizer classe $0$
### Fronteira de decisão
- A linha em que $h_\theta(x) = 0.5$ (ou que $\theta^\intercal x = 0$) é a fronteira de decisão.
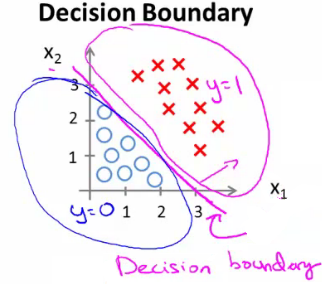
### Fronteira de decisão não linear
- Se adicionarmos novos atributos que fazem uma transformação não linear nos dados (como na aula passada, em que fizemos regressão polinomial adicionando atributos do tipo $x^k$)
- Por exemplo, se adicionarmos atributos quadráticos, podemos ter fronteiras de decisão do tipo
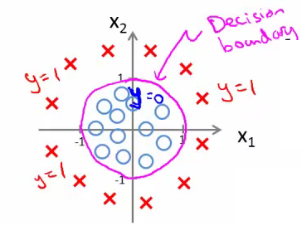
### função de custo para regressão logística
- Nossa hipótese é
$$h_\theta(z) = \frac{1}{1+e^{-\theta^\intercal x}} $$
- Na regressão linear temos que
$$J(\theta) = \frac{1}{m}\sum_i^m Cost(h_\theta(x),y)$$
Em que o custo é definido como:
$$Cost(h_\theta(x),y) = \frac{1}{2} (h_\theta(x)-y)^2 $$
### função de custo para regressão logística
- Podemos usar a mesma função de custo para regressão logistica?
- Essa função de custo é não convexa (a função da nosso hipótese (sigmoid) é não linear)
- Ao tentar miniminar, podemos ter muitos mínimos locais
- O algoritmo da descida do gradiente pode não encontrar os melhores valores para $\theta$
- Temos uma função convexa para por no lugar?
### função de custo para regressão logística
- Uma função de custo convexa:
$$
Cost(h_\theta(x),y) = \begin{cases}
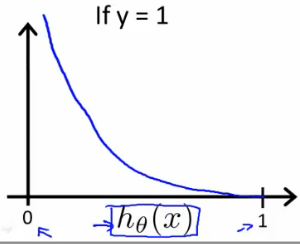
-log(h_\theta(x)) & se y=1\\
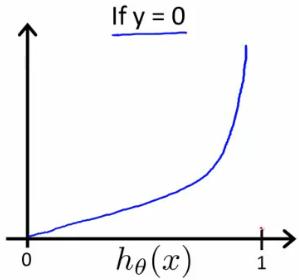
-log(1-h_\theta(x)) & se y=0
\end{cases}
$$
### função de custo para regressão logística
### função de custo para regressão logística
- Como só temos duas classes, podemos escrever a função de custo de uma maneira mais compacta:
$$
Cost(h_\theta(x),y) = -ylog(h_\theta(x)) - (1-y)log(1-h_\theta(x))
$$
- Essa função pode ser derivada da estatística, usando o princípio da estimação da máxima verossimilhança
- Assume que existe uma distribuição Gaussiana dos atributos
- É convexa
### Gradiente descendente para regressão logistica
- Podemos usar o gradiente descendente para encontrar $\theta$ na regressão logística
$$ \theta := \theta - \alpha \sum_i^m (h_\theta(x^i) - y^i)x^i$$
- Essa equação é a mesma da regressão linear
- A única diferença é que agora usamos uma hipótese diferente
- Colocar os atributos na mesma escala também pode ser necessário
### Além do gradiente descendente
- Existem outras possíveis maneiras de minizar a função de custo
- [Gradiente conjugado](https://pt.wikipedia.org/wiki/Método_do_gradiente_conjugado)
- [BFGS](https://en.wikipedia.org/wiki/Broyden–Fletcher–Goldfarb–Shanno_algorithm)
- [L-BFGS](https://en.wikipedia.org/wiki/Limited-memory_BFGS)
- ...
- São algoritmos mais complexos e otimizados, que podem ser aplicados à mesma entrada e função de custo
### Além do gradiente descendente
- Vantagens:
- Não precisamos ajustar $\alpha$ (taxa de aprendizado) manualmente
- Testam vários $\alpha$ internamente para escolher o mais adequado (além de outras melhorias)
- Em geral, mais rápidos que o gradiente descendente
- Desvantagens
- Difícil "acompanhamento"
- Difícil implementação
- Diferentes bibliotecas usam diferentes otimizações (desempenho diferente)
### Regressão logística multiclasse
- Poblemas multiclasse: mais de duas classes
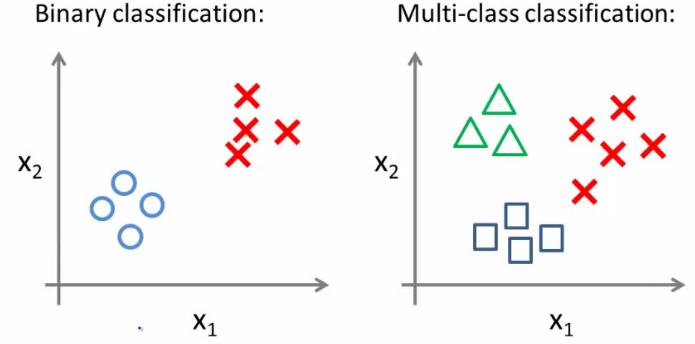
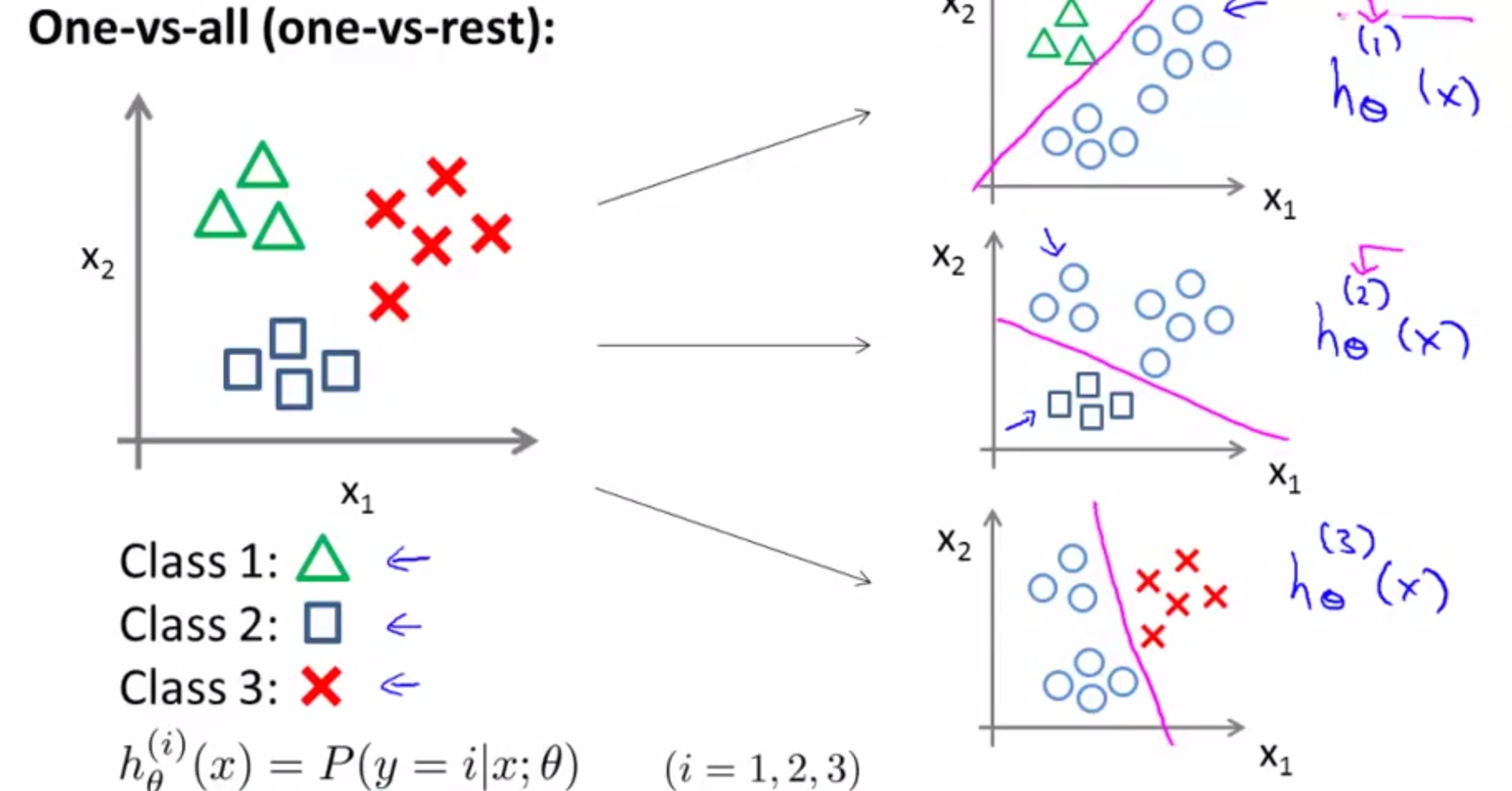
### Regressão logística multiclasse
- Estratégia "um contra todos" (*one-versus-all* ou *one-versus-rest*)
- Dividir o conjunto de dados em diversos problemas de classificação (igual ao número de classes)
- Em cada problema, uma das classes é a positiva, e as demais são agrupadas na negativa
- Escolher a classe que maximiza $P(y=1 | x_k; \theta)$, em que $k$ é a classe positiva no problema de classificação $k$
### Regressão logística multiclasse