---
presentation:
theme: beige.css
slideNumber: true
width: 1024
height: 768
---
## Aprendizado de Máquina
##### Prof. Ronaldo Cristiano Prati
[ronaldo.prati@ufabc.edu.br](mailto:ronaldo.prati@ufabc.edu.br)
###### Bloco A, Sala 513-2
### Desempenho
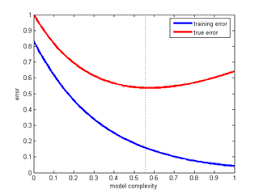
- Quando treinamos um algoritmo de aprendizado, geralmente queremos otimizar o desempenhos (e.g., minimizar o erro)
- Podemos pensar que um erro pequeno é bom, mas isso não necessariamente significa um bom modelo
- Podemos estar causando um **overfitting** nos dados
- O modelo se sai bem nos dados de treino, mas não generaliza bem
### Conjunto de teste
- Uma abordagem comum para avaliar o desempenho é utilizar um conjunto separado de teste
- Uma estratégia comum é dividir o nosso conjunto de dados em duas partes:
- Uma parte é o **conjunto de treino**
- Segunda parte é o **conjunto de teste**
- Uma divisão típica é 70%:30% (treino:teste), ou 2/3:1/3
### Validação cruzada
- Usar uma única divisão de treino e teste pode ter alguns problemas:
- O éxemplo só é usado ou para treinar ou para testar
- E se no conjunto de teste só aparecerem exemplos "fáceis"?
- Alguns exemplos "importantes" podem não ser vistos pelo algoritmo.
- O modelo é robusto a variações nos dados?
### Validação cruzada
- Validação cruzada visa contornar esses problemas:
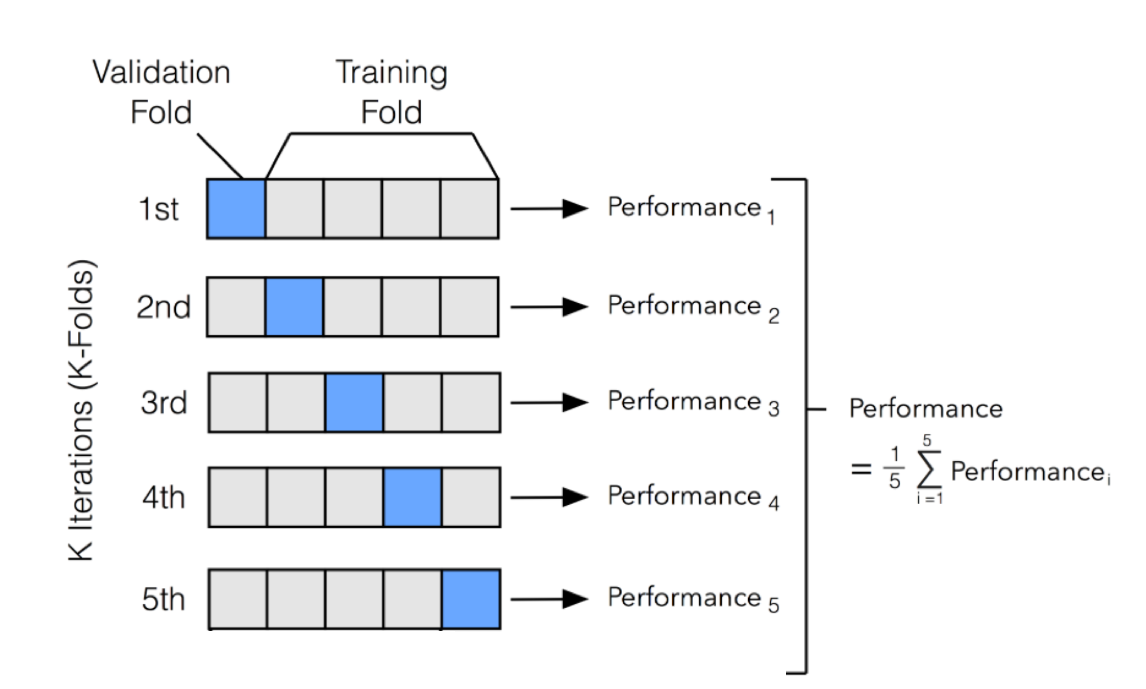
- Validação cruzada em $k$ pastas ($k$-fold cross validation)
- Dividir o conjunto de dados em $k$ partes
- Repetir o treinamento/teste $k$ vezes
- A cada iteração, umsar uma parte diferente para testar, e as outras $k-1$ para treinar
- O desempenho é calculado como a média das $k$ repetiçoes
### Validação cruzada K-fold
### Bias e variância
- Quando analizamos o desempenho de um modelo de predição, é importante entender as fontes de erro
- Existe um compromisso entre duas fontes: **bias** e **variância**
- Bias: erro sistemático devido à suposições feitas pelo algoritmo
- Variância: erro devido à características particulares dos dados de treinamento
- Erro irredutível: erros "inerentes" ao problema (por exemplo, devido a falta de informação relevante nos dados)
### Bias e variância
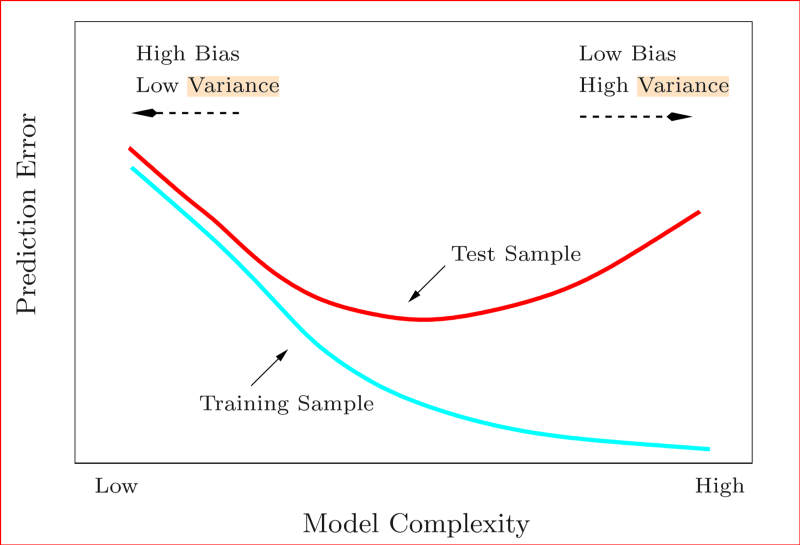
 ### Bias e variância
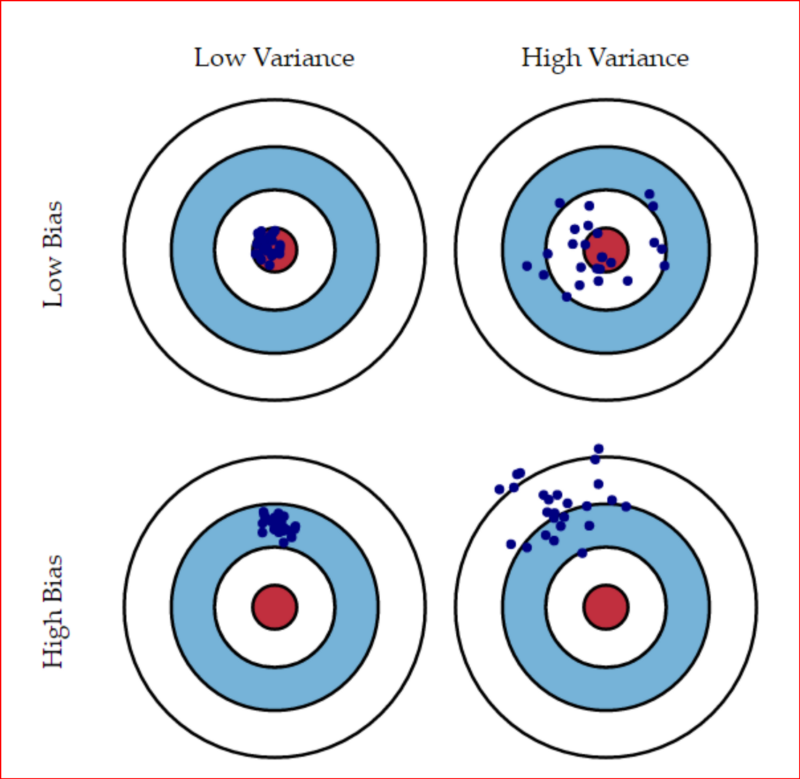
- Um modelo com alto bias pode ser muito simples para o problema
- Um modelo com alta variância tende a super ajustar aos dados de treinamento, e não generalizar o suficiente para novos dados
### Bias e variância
### Exemplo - regressão linear
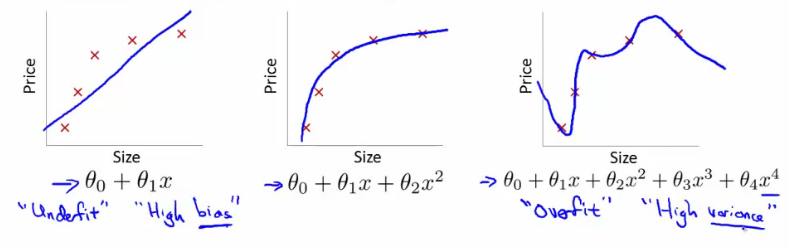
### Exemplo - regressão linear
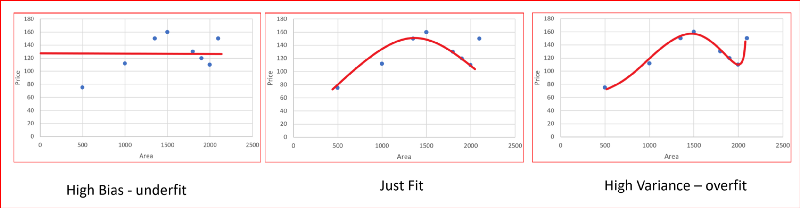
- Usar uma função linear temos **underfitting** (alto bias). O modelo não é bom
- Usar um polinômio 2o. grau funciona bem para esse problema em particular
- Polinômio 4o. grau o modelo super-ajusta aos dados de treino **overfitting** (alta variância)
### Exemplo - regressão logística
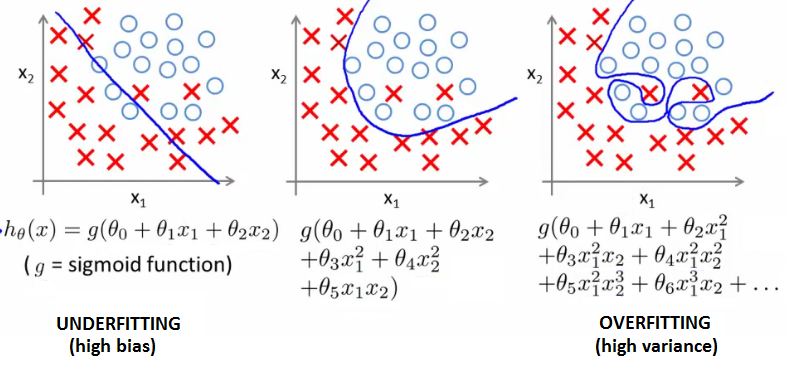
### Exemplo - regressão logística
- A função sigmoide não se ajusta bem aos dados
- Um polinômio de grau 2 funciona bem para esse problema em particular
- Um polinômio de grau maior superajusta aos dados
### Lidando com overfitting
- Em problemas reais, nem sempre é possível visualizar os dados para verificar se está ocorrendo overfitting
- Em geral, temos muitos atributos (não é só um problema de ajustar o grau do polinômio)
- Se temos poucos exemplos, o problema pode ser mais difícil de lidar
### Lidando com overfitting
1. Reduzir o número de atributos:
- Manualmente selecionar quais atributos manter
- Usar algum procedimento de seleção de atributos (voltaremos a esse ponto mais adiante)
- Eventualmente pode descartar informação relevante
2. Regularização
- Manter todos os atributos, mas controlar a magnitude dos parâmetros $\theta$
- Limita a contribuição de cada atributo na predição de $y$
### Regularização
- Ideia: alterar a função de custo para que alguns valores $\theta$ sejam pequenos
- Por exemplo, se adicionarmos uma penalização a $\theta_3$ e $\theta_4$ ao ajustar um polinômio de 4o. grau, esses coeficientes ficarão perto de zero, e teremos uma função quase quadrática
$$\min_\theta\frac{1}{2m}\sum_{i=1}^m (h\theta(x) - y)^2 + 1000 (\theta_3^2 + \theta_4^2) $$
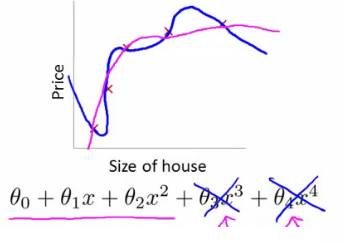
### Regularização
- Valores pequenos para parâmetro correspondem a hipóteses mais simples (eventualmente, alguns termos desaparecem)
- Uma hipótese mais simples é menos sucetível a overfitting
### Regularização
- Como escolhemos quais parâmetros penalizar?
- Em geral, adicionamos um termo que penaliza todos os parâmetros
- Por convenção, $\theta_0$ geralmente não é penalizado (mas terá pouco impacto se você incluir esse termo na regularização)
- Adicionamos um termo extra ao final da função de custo:
$$J(\theta) = \frac{1}{2m}\sum_{i=i}^m (h\theta(x^i) - y^i)^2 + \lambda \sum_{j=1}^n \theta_j $$
### Regularização
- $\lambda$ é um parâmetro de regularização
- Ele controla o compromisso entre
1. Criar um bom modelo para o conjunto de dados
2. Manter os valores the $\theta$ baixos
- Se $\lambda$ for muito alto, penalizamos todos os parâmetros (todos os $\theta$ próximos a zero) e podemos ter underfitting
- Se $\lambda$ for muito baixo, a regularização tem pouca efitividade e podemos ter overfitting
### Regressão linear regularizada
- O gradiente da função regularizada é dado por:
$$
\frac{\partial}{\partial \theta_j}J(\theta) = \frac{1}{m} \sum_{i=1}^m(h\theta(x^i) -y^i)x_j^i + \frac{\lambda}{m}\theta_j
$$
- O que nos leva a uma atualização de $\theta$:
$$
\theta_j := \theta_j (1-\alpha\frac{\lambda}{m}) - \alpha \frac{1}{m} \sum_{i=1}^m(h\theta(x^i) -y^i)x_j^i
$$
### Regressão linear regularizada
- Qual é o efeito da regularização?
- O termo $(1 - \alpha\frac{\lambda}{m})$ geralmente é um número ligeiramente menor que 1. $m$ é geralmente grande, e $\alpha$ e $\lambda$ são geralmente pequenos. Então temos (1 - número pequeno). Então esse termo gira em torno de 0.95 a 0.99, tipicamente.
- Isso faz com que o termo $\theta_j$ decresça um pouco de uma iteração para outra.
- O outro termo é exatametne igual ao gradiente descendente original
### Regressão linear regularizada
- Equação Normal, adiciona um termo extra $\lambda$ multiplicado pela (n+1) matriz identidade:
$$
\theta = \left(x^\intercal x + \lambda
\begin{bmatrix}
0 & \dots & 0 & 0 & 0 \\
0 & 1 & 0 & \dots & 0 \\
& & \dots & \\
0 & \dots & 0 & 0 & 1
\end{bmatrix}
\right)^{-1} x^\intercal y
$$
### Regressão logistica regularizada
- É similar ao caso da regressão linear, mas usando a função de custo da regressão logística
$$J(\theta) = \frac{1}{2m}\sum_{i=i}^m Cost(h_\theta(x),y) + \lambda \sum_{j=1}^n \theta_j$$
- em que:
$$ Cost(h_\theta(x),y) = -ylog(h_\theta(x)) - (1-y)log(1-h_\theta(x)) $$
- A derivada tem um formato parecido com a regressão linear (com a devida função de custo)
### Tentativas para melhorar o modelo
- Aumentar o conjunto de dados
- Tentar selecionar os melhores atributos
- Buscar novos atributos
- Realizar transformações nos dados (e.g., atributos polinomiais)
- Combinar atributos
- Ajustar o valor de $\lambda$
### Curva de aprendizado
- Pode ser útil para identificar a causa dos erros
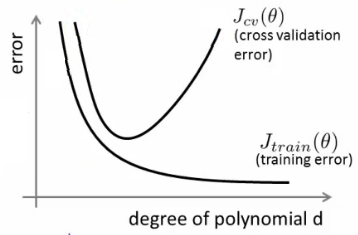
### Curva de aprendizado
- Outras opções:
- Erro x tamanho do conjunto de treino
Temos um problema de variância?
- Erro x $\lambda$
Temos um problema de bias?
### Curva de aprendizado
### Bias e variância
- Um modelo com alto bias pode ser muito simples para o problema
- Um modelo com alta variância tende a super ajustar aos dados de treinamento, e não generalizar o suficiente para novos dados

### Bias e variância

### Exemplo - regressão linear

### Exemplo - regressão linear
- Usar uma função linear temos **underfitting** (alto bias). O modelo não é bom
- Usar um polinômio 2o. grau funciona bem para esse problema em particular
- Polinômio 4o. grau o modelo super-ajusta aos dados de treino **overfitting** (alta variância)
### Exemplo - regressão logística

### Exemplo - regressão logística
- A função sigmoide não se ajusta bem aos dados
- Um polinômio de grau 2 funciona bem para esse problema em particular
- Um polinômio de grau maior superajusta aos dados
### Lidando com overfitting
- Em problemas reais, nem sempre é possível visualizar os dados para verificar se está ocorrendo overfitting
- Em geral, temos muitos atributos (não é só um problema de ajustar o grau do polinômio)
- Se temos poucos exemplos, o problema pode ser mais difícil de lidar
### Lidando com overfitting
1. Reduzir o número de atributos:
- Manualmente selecionar quais atributos manter
- Usar algum procedimento de seleção de atributos (voltaremos a esse ponto mais adiante)
- Eventualmente pode descartar informação relevante
2. Regularização
- Manter todos os atributos, mas controlar a magnitude dos parâmetros $\theta$
- Limita a contribuição de cada atributo na predição de $y$
### Regularização
- Ideia: alterar a função de custo para que alguns valores $\theta$ sejam pequenos
- Por exemplo, se adicionarmos uma penalização a $\theta_3$ e $\theta_4$ ao ajustar um polinômio de 4o. grau, esses coeficientes ficarão perto de zero, e teremos uma função quase quadrática
$$\min_\theta\frac{1}{2m}\sum_{i=1}^m (h\theta(x) - y)^2 + 1000 (\theta_3^2 + \theta_4^2) $$

### Regularização
- Valores pequenos para parâmetro correspondem a hipóteses mais simples (eventualmente, alguns termos desaparecem)
- Uma hipótese mais simples é menos sucetível a overfitting
### Regularização
- Como escolhemos quais parâmetros penalizar?
- Em geral, adicionamos um termo que penaliza todos os parâmetros
- Por convenção, $\theta_0$ geralmente não é penalizado (mas terá pouco impacto se você incluir esse termo na regularização)
- Adicionamos um termo extra ao final da função de custo:
$$J(\theta) = \frac{1}{2m}\sum_{i=i}^m (h\theta(x^i) - y^i)^2 + \lambda \sum_{j=1}^n \theta_j $$
### Regularização
- $\lambda$ é um parâmetro de regularização
- Ele controla o compromisso entre
1. Criar um bom modelo para o conjunto de dados
2. Manter os valores the $\theta$ baixos
- Se $\lambda$ for muito alto, penalizamos todos os parâmetros (todos os $\theta$ próximos a zero) e podemos ter underfitting
- Se $\lambda$ for muito baixo, a regularização tem pouca efitividade e podemos ter overfitting
### Regressão linear regularizada
- O gradiente da função regularizada é dado por:
$$
\frac{\partial}{\partial \theta_j}J(\theta) = \frac{1}{m} \sum_{i=1}^m(h\theta(x^i) -y^i)x_j^i + \frac{\lambda}{m}\theta_j
$$
- O que nos leva a uma atualização de $\theta$:
$$
\theta_j := \theta_j (1-\alpha\frac{\lambda}{m}) - \alpha \frac{1}{m} \sum_{i=1}^m(h\theta(x^i) -y^i)x_j^i
$$
### Regressão linear regularizada
- Qual é o efeito da regularização?
- O termo $(1 - \alpha\frac{\lambda}{m})$ geralmente é um número ligeiramente menor que 1. $m$ é geralmente grande, e $\alpha$ e $\lambda$ são geralmente pequenos. Então temos (1 - número pequeno). Então esse termo gira em torno de 0.95 a 0.99, tipicamente.
- Isso faz com que o termo $\theta_j$ decresça um pouco de uma iteração para outra.
- O outro termo é exatametne igual ao gradiente descendente original
### Regressão linear regularizada
- Equação Normal, adiciona um termo extra $\lambda$ multiplicado pela (n+1) matriz identidade:
$$
\theta = \left(x^\intercal x + \lambda
\begin{bmatrix}
0 & \dots & 0 & 0 & 0 \\
0 & 1 & 0 & \dots & 0 \\
& & \dots & \\
0 & \dots & 0 & 0 & 1
\end{bmatrix}
\right)^{-1} x^\intercal y
$$
### Regressão logistica regularizada
- É similar ao caso da regressão linear, mas usando a função de custo da regressão logística
$$J(\theta) = \frac{1}{2m}\sum_{i=i}^m Cost(h_\theta(x),y) + \lambda \sum_{j=1}^n \theta_j$$
- em que:
$$ Cost(h_\theta(x),y) = -ylog(h_\theta(x)) - (1-y)log(1-h_\theta(x)) $$
- A derivada tem um formato parecido com a regressão linear (com a devida função de custo)
### Tentativas para melhorar o modelo
- Aumentar o conjunto de dados
- Tentar selecionar os melhores atributos
- Buscar novos atributos
- Realizar transformações nos dados (e.g., atributos polinomiais)
- Combinar atributos
- Ajustar o valor de $\lambda$
### Curva de aprendizado
- Pode ser útil para identificar a causa dos erros

### Curva de aprendizado
- Outras opções:
- Erro x tamanho do conjunto de treino
Temos um problema de variância?
- Erro x $\lambda$
Temos um problema de bias?
### Curva de aprendizado
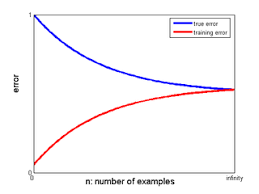
 ### Bias e variância
- Um modelo com alto bias pode ser muito simples para o problema
- Um modelo com alta variância tende a super ajustar aos dados de treinamento, e não generalizar o suficiente para novos dados

### Bias e variância

### Exemplo - regressão linear

### Exemplo - regressão linear
- Usar uma função linear temos **underfitting** (alto bias). O modelo não é bom
- Usar um polinômio 2o. grau funciona bem para esse problema em particular
- Polinômio 4o. grau o modelo super-ajusta aos dados de treino **overfitting** (alta variância)
### Exemplo - regressão logística

### Exemplo - regressão logística
- A função sigmoide não se ajusta bem aos dados
- Um polinômio de grau 2 funciona bem para esse problema em particular
- Um polinômio de grau maior superajusta aos dados
### Lidando com overfitting
- Em problemas reais, nem sempre é possível visualizar os dados para verificar se está ocorrendo overfitting
- Em geral, temos muitos atributos (não é só um problema de ajustar o grau do polinômio)
- Se temos poucos exemplos, o problema pode ser mais difícil de lidar
### Lidando com overfitting
1. Reduzir o número de atributos:
- Manualmente selecionar quais atributos manter
- Usar algum procedimento de seleção de atributos (voltaremos a esse ponto mais adiante)
- Eventualmente pode descartar informação relevante
2. Regularização
- Manter todos os atributos, mas controlar a magnitude dos parâmetros $\theta$
- Limita a contribuição de cada atributo na predição de $y$
### Regularização
- Ideia: alterar a função de custo para que alguns valores $\theta$ sejam pequenos
- Por exemplo, se adicionarmos uma penalização a $\theta_3$ e $\theta_4$ ao ajustar um polinômio de 4o. grau, esses coeficientes ficarão perto de zero, e teremos uma função quase quadrática
$$\min_\theta\frac{1}{2m}\sum_{i=1}^m (h\theta(x) - y)^2 + 1000 (\theta_3^2 + \theta_4^2) $$

### Regularização
- Valores pequenos para parâmetro correspondem a hipóteses mais simples (eventualmente, alguns termos desaparecem)
- Uma hipótese mais simples é menos sucetível a overfitting
### Regularização
- Como escolhemos quais parâmetros penalizar?
- Em geral, adicionamos um termo que penaliza todos os parâmetros
- Por convenção, $\theta_0$ geralmente não é penalizado (mas terá pouco impacto se você incluir esse termo na regularização)
- Adicionamos um termo extra ao final da função de custo:
$$J(\theta) = \frac{1}{2m}\sum_{i=i}^m (h\theta(x^i) - y^i)^2 + \lambda \sum_{j=1}^n \theta_j $$
### Regularização
- $\lambda$ é um parâmetro de regularização
- Ele controla o compromisso entre
1. Criar um bom modelo para o conjunto de dados
2. Manter os valores the $\theta$ baixos
- Se $\lambda$ for muito alto, penalizamos todos os parâmetros (todos os $\theta$ próximos a zero) e podemos ter underfitting
- Se $\lambda$ for muito baixo, a regularização tem pouca efitividade e podemos ter overfitting
### Regressão linear regularizada
- O gradiente da função regularizada é dado por:
$$
\frac{\partial}{\partial \theta_j}J(\theta) = \frac{1}{m} \sum_{i=1}^m(h\theta(x^i) -y^i)x_j^i + \frac{\lambda}{m}\theta_j
$$
- O que nos leva a uma atualização de $\theta$:
$$
\theta_j := \theta_j (1-\alpha\frac{\lambda}{m}) - \alpha \frac{1}{m} \sum_{i=1}^m(h\theta(x^i) -y^i)x_j^i
$$
### Regressão linear regularizada
- Qual é o efeito da regularização?
- O termo $(1 - \alpha\frac{\lambda}{m})$ geralmente é um número ligeiramente menor que 1. $m$ é geralmente grande, e $\alpha$ e $\lambda$ são geralmente pequenos. Então temos (1 - número pequeno). Então esse termo gira em torno de 0.95 a 0.99, tipicamente.
- Isso faz com que o termo $\theta_j$ decresça um pouco de uma iteração para outra.
- O outro termo é exatametne igual ao gradiente descendente original
### Regressão linear regularizada
- Equação Normal, adiciona um termo extra $\lambda$ multiplicado pela (n+1) matriz identidade:
$$
\theta = \left(x^\intercal x + \lambda
\begin{bmatrix}
0 & \dots & 0 & 0 & 0 \\
0 & 1 & 0 & \dots & 0 \\
& & \dots & \\
0 & \dots & 0 & 0 & 1
\end{bmatrix}
\right)^{-1} x^\intercal y
$$
### Regressão logistica regularizada
- É similar ao caso da regressão linear, mas usando a função de custo da regressão logística
$$J(\theta) = \frac{1}{2m}\sum_{i=i}^m Cost(h_\theta(x),y) + \lambda \sum_{j=1}^n \theta_j$$
- em que:
$$ Cost(h_\theta(x),y) = -ylog(h_\theta(x)) - (1-y)log(1-h_\theta(x)) $$
- A derivada tem um formato parecido com a regressão linear (com a devida função de custo)
### Tentativas para melhorar o modelo
- Aumentar o conjunto de dados
- Tentar selecionar os melhores atributos
- Buscar novos atributos
- Realizar transformações nos dados (e.g., atributos polinomiais)
- Combinar atributos
- Ajustar o valor de $\lambda$
### Curva de aprendizado
- Pode ser útil para identificar a causa dos erros

### Curva de aprendizado
- Outras opções:
- Erro x tamanho do conjunto de treino
Temos um problema de variância?
- Erro x $\lambda$
Temos um problema de bias?
### Curva de aprendizado
### Bias e variância
- Um modelo com alto bias pode ser muito simples para o problema
- Um modelo com alta variância tende a super ajustar aos dados de treinamento, e não generalizar o suficiente para novos dados

### Bias e variância

### Exemplo - regressão linear

### Exemplo - regressão linear
- Usar uma função linear temos **underfitting** (alto bias). O modelo não é bom
- Usar um polinômio 2o. grau funciona bem para esse problema em particular
- Polinômio 4o. grau o modelo super-ajusta aos dados de treino **overfitting** (alta variância)
### Exemplo - regressão logística

### Exemplo - regressão logística
- A função sigmoide não se ajusta bem aos dados
- Um polinômio de grau 2 funciona bem para esse problema em particular
- Um polinômio de grau maior superajusta aos dados
### Lidando com overfitting
- Em problemas reais, nem sempre é possível visualizar os dados para verificar se está ocorrendo overfitting
- Em geral, temos muitos atributos (não é só um problema de ajustar o grau do polinômio)
- Se temos poucos exemplos, o problema pode ser mais difícil de lidar
### Lidando com overfitting
1. Reduzir o número de atributos:
- Manualmente selecionar quais atributos manter
- Usar algum procedimento de seleção de atributos (voltaremos a esse ponto mais adiante)
- Eventualmente pode descartar informação relevante
2. Regularização
- Manter todos os atributos, mas controlar a magnitude dos parâmetros $\theta$
- Limita a contribuição de cada atributo na predição de $y$
### Regularização
- Ideia: alterar a função de custo para que alguns valores $\theta$ sejam pequenos
- Por exemplo, se adicionarmos uma penalização a $\theta_3$ e $\theta_4$ ao ajustar um polinômio de 4o. grau, esses coeficientes ficarão perto de zero, e teremos uma função quase quadrática
$$\min_\theta\frac{1}{2m}\sum_{i=1}^m (h\theta(x) - y)^2 + 1000 (\theta_3^2 + \theta_4^2) $$

### Regularização
- Valores pequenos para parâmetro correspondem a hipóteses mais simples (eventualmente, alguns termos desaparecem)
- Uma hipótese mais simples é menos sucetível a overfitting
### Regularização
- Como escolhemos quais parâmetros penalizar?
- Em geral, adicionamos um termo que penaliza todos os parâmetros
- Por convenção, $\theta_0$ geralmente não é penalizado (mas terá pouco impacto se você incluir esse termo na regularização)
- Adicionamos um termo extra ao final da função de custo:
$$J(\theta) = \frac{1}{2m}\sum_{i=i}^m (h\theta(x^i) - y^i)^2 + \lambda \sum_{j=1}^n \theta_j $$
### Regularização
- $\lambda$ é um parâmetro de regularização
- Ele controla o compromisso entre
1. Criar um bom modelo para o conjunto de dados
2. Manter os valores the $\theta$ baixos
- Se $\lambda$ for muito alto, penalizamos todos os parâmetros (todos os $\theta$ próximos a zero) e podemos ter underfitting
- Se $\lambda$ for muito baixo, a regularização tem pouca efitividade e podemos ter overfitting
### Regressão linear regularizada
- O gradiente da função regularizada é dado por:
$$
\frac{\partial}{\partial \theta_j}J(\theta) = \frac{1}{m} \sum_{i=1}^m(h\theta(x^i) -y^i)x_j^i + \frac{\lambda}{m}\theta_j
$$
- O que nos leva a uma atualização de $\theta$:
$$
\theta_j := \theta_j (1-\alpha\frac{\lambda}{m}) - \alpha \frac{1}{m} \sum_{i=1}^m(h\theta(x^i) -y^i)x_j^i
$$
### Regressão linear regularizada
- Qual é o efeito da regularização?
- O termo $(1 - \alpha\frac{\lambda}{m})$ geralmente é um número ligeiramente menor que 1. $m$ é geralmente grande, e $\alpha$ e $\lambda$ são geralmente pequenos. Então temos (1 - número pequeno). Então esse termo gira em torno de 0.95 a 0.99, tipicamente.
- Isso faz com que o termo $\theta_j$ decresça um pouco de uma iteração para outra.
- O outro termo é exatametne igual ao gradiente descendente original
### Regressão linear regularizada
- Equação Normal, adiciona um termo extra $\lambda$ multiplicado pela (n+1) matriz identidade:
$$
\theta = \left(x^\intercal x + \lambda
\begin{bmatrix}
0 & \dots & 0 & 0 & 0 \\
0 & 1 & 0 & \dots & 0 \\
& & \dots & \\
0 & \dots & 0 & 0 & 1
\end{bmatrix}
\right)^{-1} x^\intercal y
$$
### Regressão logistica regularizada
- É similar ao caso da regressão linear, mas usando a função de custo da regressão logística
$$J(\theta) = \frac{1}{2m}\sum_{i=i}^m Cost(h_\theta(x),y) + \lambda \sum_{j=1}^n \theta_j$$
- em que:
$$ Cost(h_\theta(x),y) = -ylog(h_\theta(x)) - (1-y)log(1-h_\theta(x)) $$
- A derivada tem um formato parecido com a regressão linear (com a devida função de custo)
### Tentativas para melhorar o modelo
- Aumentar o conjunto de dados
- Tentar selecionar os melhores atributos
- Buscar novos atributos
- Realizar transformações nos dados (e.g., atributos polinomiais)
- Combinar atributos
- Ajustar o valor de $\lambda$
### Curva de aprendizado
- Pode ser útil para identificar a causa dos erros

### Curva de aprendizado
- Outras opções:
- Erro x tamanho do conjunto de treino
Temos um problema de variância?
- Erro x $\lambda$
Temos um problema de bias?
### Curva de aprendizado