Aprendizado de Máquina

Neural Networks

Prof. Ronaldo Cristiano Prati
ronaldo.prati@ufabc.edu.br
Bloco A, Sala 513-2

Modelos complexos

  • Suponha que tenhamos um problema de classificação complexo, que a regressão logística não funciona bem
  • Como vimos, uma alternativa é criar termos polinomiais
  • Se tivermos um número pequeno de atributos, a estratégia é adequada, mas e se tivermos, digamos, 100?
    • Se adicionarmos termos quadráticos, o número de novos atributos cresce na ordem de O(n2)O(n^2)!
    • Se adicionarmos termos cúbicos, o número de novos atributos cresce na ordem de O(n3)O(n^3)!
  • Precisamos de outras maneiras de criar modelos complexos.

Redes neurais

  • Redes neurais (NNs) foram originalmente motivadas como modelos para replicar a funcionalidade do cérebro
  • Já que queremos constuir um modelo de aprendizado, porque não imitar o cérebro?
    • Nosso enfoque aqui no curso é como um técnica de aprendizado de máquina

Histórico

  • Primeiro modelo nos anos 40 (McCulloch & Pitts)
  • Muita euforia, mas limitações levaram a um período de pouco avanço
  • Novos avanços entre o fim dos anos 70 e início dos anos 80 provocaram um ressurgimento
  • Muito usadas nos anos 80 e 90
  • Popularidade diminuiu no final dos anos 90 (falta de recursos computacionais)
  • Ressurgimento nos últimos anos com redes profundas

Neurônio

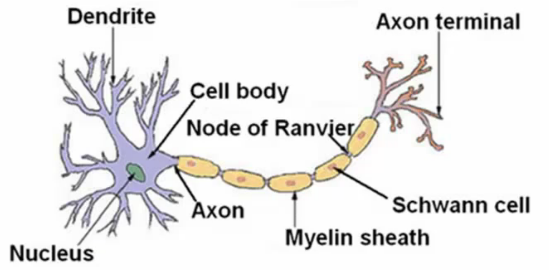
Neuronio

  • O neurônio recebe uma ou mais entradas pelos dendritos
  • Faz o processamento
  • Envia a saída para o axio
  • A comunicação é feita por meio de "spikes" elétricos (pulso elétrico pelo axônio para outros neurônios)

Neurônio Artificial

Neuronio Artificial

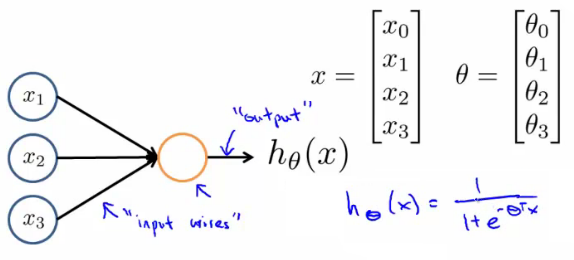
  • Em uma rede neural artificial, um neurônio é um unidade logística
    • Alimenta a rede pela conexão de entrada
    • A unidade logística faz a computação
    • Envia a saída pela conexão de saída

Neurônio Artificial

  • Um modelo muito simplificado da computação de um neurônio real
  • Normalmente inclue uma entrada x0x_0, cujo valor é igual a 1
    • Essa entrada é chamada de bias (não confundir com o bias-variância)
  • Esse é um neurônio com uma função de ativação sigmoide (logistica).
    • Outras funções de ativação pode ser usadas
  • O vetor θ\theta também é chamado de vetor de pesos do modelo.

Redes Neurais

  • Neurônios aritificiais podem ser combinados em redes neurais

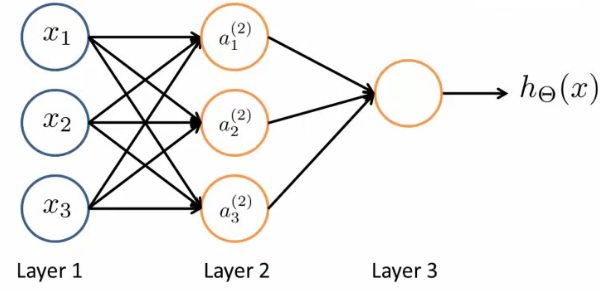
Rede Neural

Redes Neurais

  • Primeira camada é a camada de entrada
  • Camada finald é a camada de saída
    • Ela produz o valor computado pela hipótese
  • A(s) camada(s) do meio são chamadas de camadas ocultas
    • Não observamos os valores computados nas camadas intermediárias
    • Podemos ter mais de uma camada ocultas

Notação

  • aija_i^j ativação da unidade ii da camada jj
    • a12a_1^2 é a ativação da 1a. unidade da segunda camada
    • Por ativação, nos referimos ao valor que é calculado como saída daquele unidade
  • θj\theta^j matriz de parâmetros controlando a função de mapeamento da camada jj para a j+1j+1
    • Se a rede tem sjs_j nós na camada jj e sj+1s_{j+1} nós na camada j+1j+1, então θj\theta_j tem dimensões $[s_{j+1}\times s_j+1]
    • sj+1s_{j+1} nós na camada (j+1)(j+1) e sjs_j na camada jj mais o bias

Computação

  • Quais são as computações que ocorrem?
    • Temos que calcular a ativação para cada nó
    • A ativação depende de
      • A(s) entrada(s) de cada nó
      • Os parâmetros associados com cada nó (do vetor θ\theta associado a cada camada)

Computação

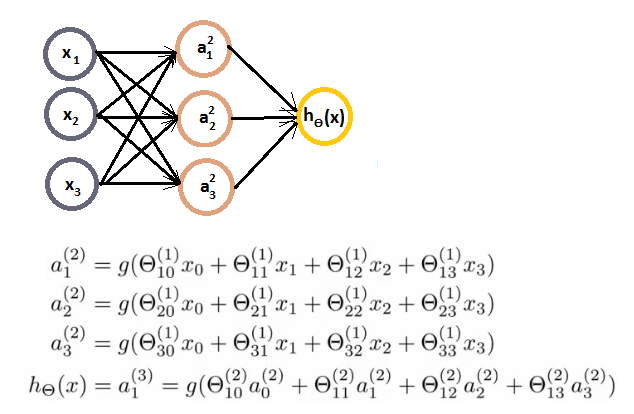
Rede Neural

Computação (vetorização)

  • A implementação (e o entendimento) de uma rede neural pode ser facilitada utilizando vetorização. Vamos definir z12z_1^2 como

z12=Ɵ101x0+Ɵ111x1+Ɵ121x2+Ɵ131x3z_1^2 = Ɵ_{10}^1 x_0 + Ɵ_{11}^1x_1 + Ɵ_{12}^1x_2 + Ɵ_ {13}^1x_3

  • Que significa a12=g(z12)a_1^2 = g(z_1^2). Similarmente, podemos definir z22z_2^2 e z32z_3^2. Podemos definir os vetores:

x=[x0x1x2x3]z2=[z12z22z32]x=\begin{bmatrix} x_0\\ x_1\\ x_2\\ x_3 \end{bmatrix} z^2=\begin{bmatrix} z_1^2\\ z_2^2\\ z_3^2 \end{bmatrix}

Computação (vetorização)

  • Podemos vetorizar a computação em 2 etapas:
    • z2=θ1xz^2 = \theta^1 x, em que θ1\theta^1 é a matriz definida anteriormente e xx o vetor de entrada
    • a2=g(z2)a^2 = g(z^2), ou seja, aplicamos g()g() ao vetor z2z^2
  • Tendo calculado a2a^2, podemos definir z3z^3 e hθ(x)=a3h_\theta(x) = a^3 como:
    • z3=θ2a2z^3 = \theta^2 a^2, em que θ1\theta^1 é a matriz definida anteriormente e xx o vetor de entrada
    • a3=g(z3)a^3 = g(z^3), ou seja, aplicamos g()g() ao vetor z3z^3

Computação (vetorização)

  • Este processo é chamado de propagação forward
  • Começa com a ativação da camada de entrada, i.e., o vetor xx como entrada
  • Propaga para frente e calcula a ativação de cada camada sequencialmente
  • Essa é uma versão vetorizada da implementação

Rede neural "aprende" sueus próprios atributos

  • A última camada é uma regressão logistica
  • Mas ao invés de ser aplicada aos atributos originais, ela é aplicada à saída aˆ2aˆ2 da camada anterior. O mesmo acontece com a camada anterior
  • Dessa maneira, ao invés de estar restrita aos atributos de entrada, a rede neural pode "aprender" seus próprios atirbutos para a regressão logística
  • Dependendo dos parâmetros de cada camada, podemos aprender combinações interessantes!
  • As camadas oculta fazem o papel de criar novos atributos, ao invés de criamos manualmente como fazíamos anteriormente

Outras configurações

  • Além da rede vista aqui, outras arquiteturas (topologias) são possíveis
    • Mais/menos nós por camada
    • Mais chamadas
    • Outras funções de ativação

XOR

  • Um exemplo simples de um problema de classificação não linar é o ou exclusivo (xor)

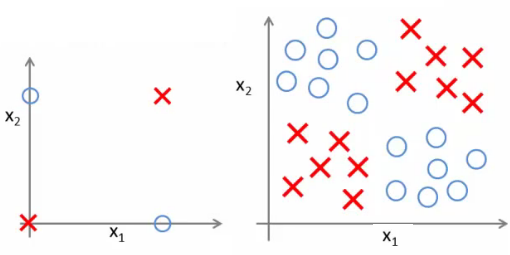
  • Esta função não pode ser computada utilizando somente um neurônio

AND

  • Vamos começar pelo exemplo de predizer x1x_1 AND x2x_2, que é o operador e lógico e só é verdade se ambos x1x_1 e x2x_2 são 1.

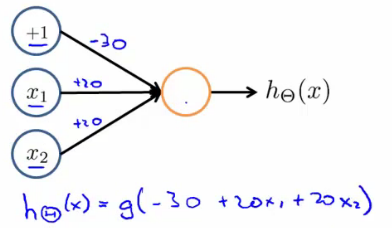
  • Depois do treinado, os pesos convergem para

Θ(1)=[−302020]\Theta^{(1)} = \begin{bmatrix}−30 & 20 & 20\end{bmatrix}

AND

hΘ(x)=g(−30+20x1+20x2)x1=0  and  x2=0  then  g(−30)≈0x1=0  and  x2=1  then  g(−10)≈0x1=1  and  x2=0  then  g(−10)≈0x1=1  and  x2=1  then  g(10)≈1\begin{aligned}& h_\Theta(x) = g(-30 + 20x_1 + 20x_2) \\ & x_1 = 0 \ \ and \ \ x_2 = 0 \ \ then \ \ g(-30) \approx 0 \\ & x_1 = 0 \ \ and \ \ x_2 = 1 \ \ then \ \ g(-10) \approx 0 \\ & x_1 = 1 \ \ and \ \ x_2 = 0 \ \ then \ \ g(-10) \approx 0 \\ & x_1 = 1 \ \ and \ \ x_2 = 1 \ \ then \ \ g(10) \approx 1\end{aligned}

Not

  • Similarmente, podemos criar uma rede para calcular o não

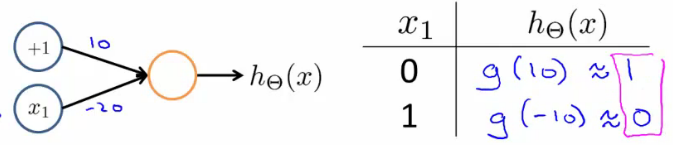
XNOR

  • Podemos combinar as duas para criar o XNOR

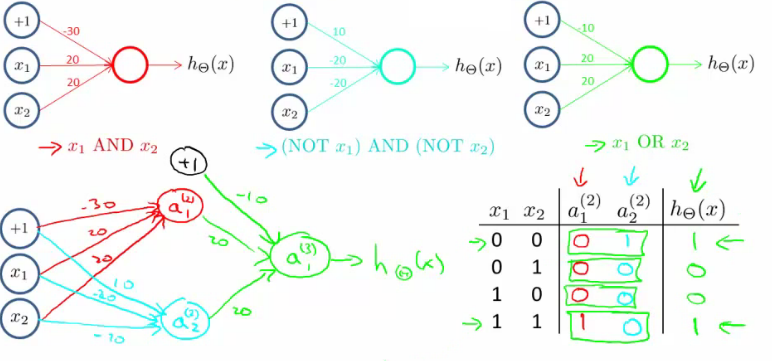
VIDEO

Video 1
Video 2

Classificação multiclasse

  • Uma extensão do "um-contra-todos"
  • A saída da rede é um vetor um nó para cada classe

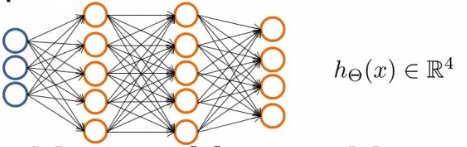
title

Classificação multiclasse

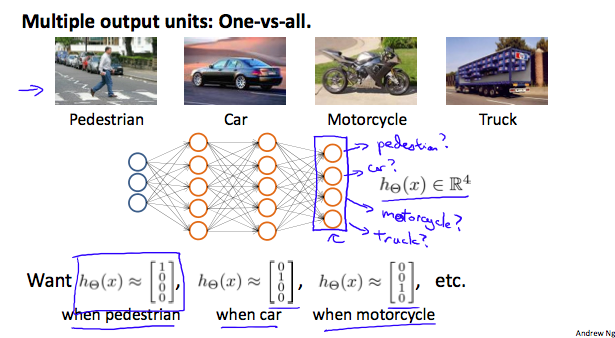
title

Classificação multiclasse

  • Redefinimos nossas classes yy como um vetor que representa uma classe diferente, com somente um 1 indicando qual é a classe, e 0 nas demais posições

title

  • As camadas internas podem ser representadas como

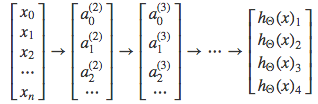
title

Classificação multiclasse

  • A hipótese dá um vetor como saída

hΘ(x)=[0010]h_\Theta(x) =\begin{bmatrix}0 \\ 0 \\ 1 \\ 0 \\ \end{bmatrix}

  • Que no nosso exemplo é a terceira classe, ou hΘ(x)=3h_\Theta(x)=3, que representa a moto.