Aprendizado de Máquina

Neural Networks (parte2)

Prof. Ronaldo Cristiano Prati
ronaldo.prati@ufabc.edu.br

Bloco A, Sala 513-2

Dados

import pickle
import numpy as np

#dados estão armezenados como um objeto python em disco usando pickle
with open('data.pkl', 'rb') as f:
    data = pickle.load(f)

data['X'].shape
#(5000,400)

data['y'].shape
#(5000,1)

Dados

# seleciona 1 aleatoriamente
ex = data['X'][np.random.randint(5000),]
# e mostra a imagem
plt.imshow(ex.reshape(20,20).T,cmap=plt.get_cmap('Greys'))

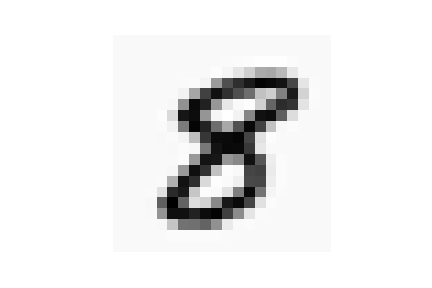
Rede

#dados estão armezenados como um objeto python em disco usando pickle
with open('weights.pkl', 'rb') as f:
    weights = pickle.load(f)

weights['Theta1'].shape
#(25, 401)

weights['Theta2'].shape
#(10,26)

Rede

• Camada 1
  

Rede

• Camada 2

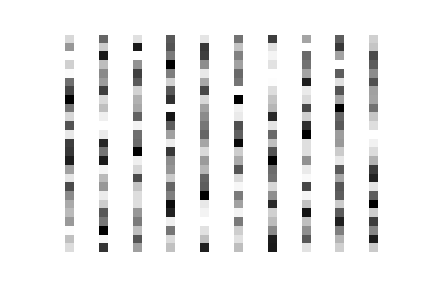
Propagação forward

from scipy.special import expit #função sigmoide vetorizada

def propagateForward(a0,Thetas):

    a = a0
    for theta in Thetas:
        a = np.insert(a,0,1,axis=0) # adiciona o bias
        z = theta.dot(a)            # z = theta * a
        a = expit(z)                # a = g(z)
    return(a)

def predict(example,Thetas):

    output = propagateForward(example,Thetas)
    return np.argmax(output,axis=0)

Testando a rede

errors = []

for i in range(len(X)):
    #classes estão no intervalo 1..10
    prediction = predict(data['X'][i,:],weights.values())+1

    if (prediction != data['y'][i,0]):
        errors.append(i)

print("Taxa de erro: ",(len(errors)*100)/5000,"%")
# Taxa de erro:  2.48 %

Testando a rede (vetorizado)

predictions = predict(data['X'].T,weights.values())+1
errors = np.where(predictions != np.ravel(data['y']))

print("Taxa de erro: ",(len(np.ravel(errors))*100)/5000,"%")

Exemplos de erros

Função de custo

• Regressão Logística (regularizada)

$J(\theta) = \frac{1}{2m}\sum_{i=i}^m -y\log(h_\theta(x)) - (1-y)\log(1-h_\theta(x)) + \lambda \sum_{j=1}^n \theta_j$

• Rede Neural

$J(\theta) = \frac{1}{2m}\sum_{i=i}^m\sum_{k=1}^{K} -y_k\log(h_\theta(x))_{k} - (1-y_k)\log(1-h_\theta(x))_k + \lambda \sum_l^L\sum_i^{s_l}\sum_{j=1}^{s_(l+1)} (\Theta_{ij}^l)^2$

Como encontramos os pesos?

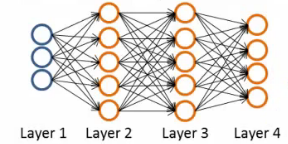
• $L$ = número de chamadas
• $s_l$ = número de nós na camada $l$ (sem contar o bias)
• $s_L = k$ = última camada tem $k$ nós, em que $k$ é o número de classes

Função de custo

• Apesar de parecer complicada, a função de custo é
  • uma média ponderada de todos os neurônios da camada de saída (primeira parte da função)
  • soma dos quadrados dos pesos das camadas da rede, também chamado de decaimento do peso (segunda parte da função).

Backpropagation

• Queremos minimizar $J(\Theta)$
• Para usar o Backpropagation, precisamos
  • Calcular a função de custo $J(\Theta)$
  • Calcular $\frac{\partial}{\partial \Theta_{ij}^l} J(\Theta)$
  • Para cada nó, podemos calcular $\delta_j^l$ - o erro referente ao nó $j$ na camada $l$

Cálculo do gradiente (intuição)

• Vamos considerar a rede de 4 camadas $(L=4)$

• Na última camada:
  $\delta_j^4 = a_j^4 - y_j$

• Ou, em notação vetorial
  $\delta^4 = a^4 - y$

• $\delta^4$ e o vetor de erros da camada 4

Cálculo do gradiente (intuição)

• Com $\delta^4$ calculado, podemos determinar o erro das outras camadas como:
  $\begin{aligned} \delta^3 & = (\Theta^3)^\intercal \delta^4 .* g'(z^3) \\ \delta^2 & = (\Theta^2)^\intercal \delta^3 .* g'(z^2) \end{aligned}$

• $g'(z^k)$ pode ser computado como $a^k .* (1-a^k)$

$\begin{aligned} \delta^3 & = (\Theta^3)^\intercal \delta^4 .* a^3 .* (1-a^3) \\ \delta^2 & = (\Theta^2)^\intercal \delta^3 .* a^2 .* (1-a^2) \end{aligned}$

Cálculo do gradiente (intuição)

• Por que calculamos esses $\delta$´s?

$\frac{\partial}{\partial \Theta_{ij}^l} J(\Theta) \propto a_j^l * \delta_i^{l+1}$

• Fazendo o backpropagation e calculando os $\delta$ podemos calcular os termos das derivadas parciais
• Podemos usar essas derivadas parciais para minimizar a função de custo.
• Podemos usar regularização se necessário

Backpropagation

1. Fazer uma passagem para a frente

2. Usar a saída da última camada e o rótulo real para calcular o erro

3. Propagar o erro para as camadas anteriores, calculando $\Delta_{ij}^l$

4. Calular o gradiente

   • $D_{ij}^l = \frac{1}{m}\Delta_{ij}^l + \lambda\Theta_{ij}^l$ (regularizada)
   • $D_{ij}^l = \frac{1}{m}\Delta_{ij}^l$ (não regularizada)

5. Podemos usar esse gradiente em algum algoritmo de otimização

Empacotando os parâmetros

• A maioria dos algoritmos de otimização não aceita como entrada matrizes
• Para contornar isso, podemos "empacotar" (unroll) e "desempacotar" os parâmetros em em vetor

Empacotando os parâmetros

def flattenParams(thetas):
    flattened = np.concatenate([theta.flatten() for theta in thetas])
    shapes = [theta.shape for theta in thetas]
    return (flattened,shapes)

def reshapeParams(flattened_array,shapes):
    begin = 0
    thetas = []
    for shape in shapes:
        end = begin+np.prod(shape)
        thetas.append(flattened_array[begin:end].reshape(shape))
        begin = end

    return np.array(thetas)

colocando tudo junto

import numpy as np
from scipy.optimize import minimize
from sklearn.preprocessing import OneHotEncoder

def train(X,y,shapes, alpha=0.01,regularize=True,maxiter=1000):
    Y=OneHotEncoder().fit_transform(y).toarray()
    initial_theta = randomParams(shapes)
    res = minimize(cost_gradient_step, initial_theta,
    args=(shapes,X,Y,alpha,regularize),
    jac=True,method='L-BFGS-B',options={'maxiter': maxiter})
    return(reshapeParams(res['x'],shapes))

shapes = np.array([(25, 401), (10, 26)])    
thetas = train(data['X'],data['y'],shapes)

Inicialização e custo

def cost(h,Y,thetas,alpha=0,regularize=True):
    m = len(Y)
    J = np.sum(np.multiply(-Y, np.log(h.T))
        - np.multiply((1 - Y), np.log(1 - h.T)))/m
    if regularize:
        J += (float(alpha) /
              (2 * m)) * (np.sum([np.sum(np.power(t[:,1:],2))
                             for t in thetas]))

    return J

def randomParams(shapes,epsilon_init=0.12):
    size = sum([np.prod(shape) for shape in shapes])
    return np.random.random(size=size)*2*epsilon_init-epsilon_init

Alterando propagateForward

• Retornamos também os valores de $a^l$ para usar no backpropagation

def propagateForward(a0,thetas):

    a = a0
    a_values = []

    for theta in thetas:
        a = np.insert(a,0,1,axis=0) #Add the bias unit
        a_values.append(a)
        z = theta.dot(a)
        a = expit(z)
    return(a_values,a)

Backpropagation

def propagateBackward(as_values,h, thetas, Y, alpha=0, regularize=True):
    L = len(as_values)
    m = len(Y)
    delta = h.T-Y
    deltas = [np.dot(delta.T,as_values[L-1].T)/m]
    for i in reversed(range(1,L)):
        g_z = np.multiply(as_values[i],(1-as_values[i]))
        delta = np.multiply(np.dot(thetas[i].T,delta.T),g_z)
        deltas.append((np.dot(delta,as_values[i-1].T)[1:,])/m)


    deltas = list(reversed(deltas))

    if regularize:
        for i in range(L):
            # não regulariza a0
            deltas[i][:, 1:] = deltas[i][:, 1:] +
            ((thetas[i][:, 1:] * alpha) / m)

    return(deltas)

Calcula uma passada nos dados

def cost_gradient_step(params,shapes,X,Y,alpha=0,regularize=True):
    thetas = reshapeParams(params,shapes)
    as_values, h = propagateForward(X.T,thetas)
    c = cost(h,Y,thetas,alpha,regularize)
    D = propagateBackward(as_values,h,thetas,Y,alpha,regularize)
    D,_ = flattenParams(D)
    return c, D

Função de custo

• Diferentemente da regressão logística (e linear), a função de custo não é convexo
• Isso significa que podemos ter mínimos locais
• Temos que testar várias topologias, parâmetro de regularização, iniciazações diferentes (rodar várias vezes)