Aprendizado de Máquina

Máquinas de vetores de suporte (SVM's)

Prof. Ronaldo Cristiano Prati

ronaldo.prati@ufabc.edu.br

Bloco A, sala 513-2

SVM's

  • Máquinas de vetores de suporte são uma outra família de algoritmos de aprendizado de máquina supervisionado
    • Em certos casos, é mais simples de usar que redes neurais
    • Também tem ótimo desempenho em certas aplicações

Função de custo

  • Relembramos da função de custo da regressão logística:

J(θ)=1m∑im−yilog⁡(hθ(xi))−(1−yi)log⁡(1−hθ(xi))+λ2m∑j=1nθ2J(\theta) = \frac{1}{m} \sum_i^m - y^i \log (h_\theta(x^i)) - (1- y_i)\log (1-h_\theta(x^i)) + \frac{\lambda}{2m} \sum_{j=1}^n\theta^2

  • Na regressão logística queremos:
    • se y=1y=1, hθ(x)≈1h_\theta(x)\approx 1 e θ⊺x>0\theta^\intercal x > 0
    • se y=0y=0, hθ(x)≈0h_\theta(x)\approx 0 e θ⊺x<0\theta^\intercal x < 0

Função de custo

Quando y=1y=1

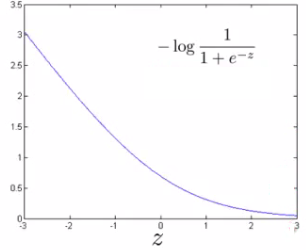
Quando y=0y=0

Função de custo - SVM

Quando y=1y=1

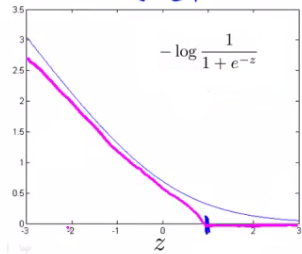
cost1(z)cost_1(z)

Quando y=0y=0


cost0(z)cost_0(z)

Função de custo completa - SVM

  • Removemos 1m\frac{1}{m} (convenção, não altera o mínimo)
  • Parâmetro de regularização associado ao primeiro termo (razão mais adiante)

min⁡θC∑im−yicost1(hθ(xi))−(1−yi)cost0(1−hθ(xi))+12∑j=1nθ2\min_{\theta} C \sum_i^m - y^i cost_1 (h_\theta(x^i)) - (1- y_i) cost_0 (1-h_\theta(x^i)) + \frac{1}{2} \sum_{j=1}^n\theta^2

Função de custo completa - SVM

  • O parâmetro CC pode é equivalente a 1λ\frac{1}{\lambda}.

    • Se quisermos regulizarar mais (reduzir overfitting), decrescemos CC
    • Se quisermos regularizar menos (reduzir underfitting), aumentados CC

  • Ao contrário da regressão logística, a saída de hθ(x)h_\theta(x) é somente 0 ou 1 (não uma probabilidade)

Maximização da margem

  • SVM também é conhecida como classificador de margem larga

  • Em SVM queremos:

    • se y=1y=1, θ⊺x≥1\theta^\intercal x \geq 1 (não apenas >0>0)
    • se y=0y=0, θ⊺x≤−1\theta^\intercal x \leq -1 (não apenas <0<0)

Maximização da margem

  • Para entender o efeito, vamos considerar um valor de CC muito grande
  • Nesse caso ∑θ2\sum\theta^2 predomina na função de custo, que resulta no problema

min⁡θ12∑inθ2s.a.θ⊺x≥1 se y=1θ⊺x≤−1 se y=0\begin{aligned} \min_\theta & \frac{1}{2} \sum_i^n \theta^2\\ s.a. & \theta^\intercal x \geq 1 \text{ se } y=1 \\ & \theta^\intercal x \leq -1 \text{ se } y=0 \\ \end{aligned}

Maximização da margem

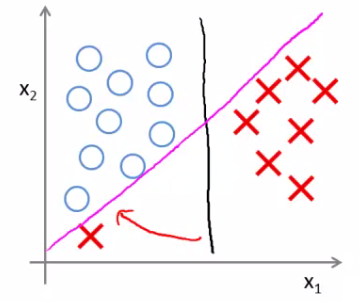
  • Esse problema corresponde a encontrar a fronteira de decisão que maximiza a margem de separação entre as classes

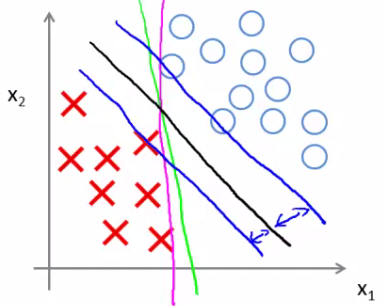
Maximização da margem

  • O parâmetro de regularização CC ajuda a contornar outliers

CC adequado

CC muito grande

Maximização da margem

  • Por que a margem é maximizada?
  • Vamos analisar intuitivamente
    • Vamos considerar um problema com 2 dimensões (é mais fácil desenhar)
    • Vamos desconsiderar θ0\theta_0 por hora
    • Vamos considerar também um problema linearmente separável

Maximização da margem

  • Relembre que queremos min⁡θ12∑inθ2\min_\theta \frac{1}{2} \sum_i^n \theta^2

    • Vamos reescrever ∑inθ2\sum_i^n \theta^2:
      ∑θ2=(θ12+θ22)=(θ1+θ2)2=∥θ∥2\begin{aligned} \sum \theta^2 & = (\theta_1^2 +\theta_2^2)\\ & = \left(\sqrt{\theta_1 +\theta_2}\right)^2\\ & = \lVert\theta\rVert^2 \end{aligned}
    • em que ∥θ∥2\lVert\theta\rVert^2 é a norma (tamanho) do vetor

Maximização da margem

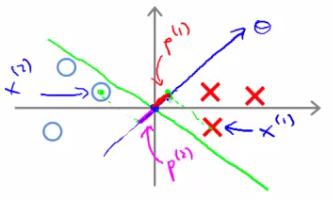
  • O que θ⊺x\theta^\intercal x faz?
    θ⊺xi=[θ1θ2][x1ix2i]=θ1x1+θ2x2=⟨θ,xi⟩=pi∥θ∥\begin{aligned} \theta^\intercal x^i &= \begin{bmatrix} \theta_1\\ \theta_2 \end{bmatrix} [x_1^i x_2^i] \\ & = \theta_1 x_1 + \theta_2 x_2 \\ & = \langle \theta,x^i\rangle \\ & = p^i\lVert\theta\rVert \end{aligned}
  • em que ⟨θ,xi⟩\langle \theta,x^i\rangle é o produto interno entre θ\theta e xix^i, e pip^i é o comprimento da projeção de xix^i em θ\theta.

Maximização da margem

  • As restrições
    θ⊺x≥1 se y=1θ⊺x≤−1 se y=0\theta^\intercal x \geq 1 \text{ se } y=1 \\ \theta^\intercal x \leq -1 \text{ se } y=0
    podem ser reinterpretadas como
    pi∥θ∥≥1 se y=1pi∥θ∥≤−1 se y=0p^i\lVert\theta\rVert \geq 1 \text{ se } y=1 \\ p^i\lVert\theta\rVert \leq -1 \text{ se } y=0

Maximização da margem

  • Se a margem entre as classes for pequena

Margem pequena

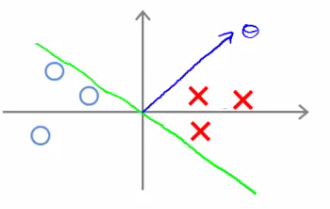
Projeção pequena

Maximização da margem

  • Se a margem entre as classes for grande

    Margem grande

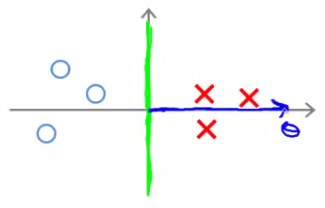
    Projeção maximizada

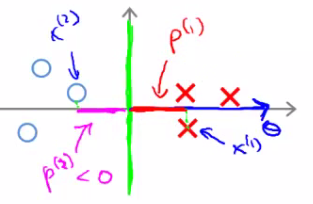
Maximização da margem

  • Se pp é pequeno, ∥θ∥\lVert\theta\rVert tem que ser grande para garantir as restrições.

  • Mas queremos minimizar ∥θ∥2\lVert\theta\rVert^2!

  • Maximizar pp minimiza ∥θ∥\lVert\theta\rVert

Maximização da margem

  • Inicialmente ignoramos θ0\theta_0
    • A fronteira de decisão deve passar obrigatóriamente pela origem
  • Se θ0\theta_0 puder assumir outros valores, não temos a restrição da fronteira de decisão passar pela origem
  • Os princípios gerais continuam os mesmos

Kernel

  • O kernel é útil quando queremos computar uma fronteira de decisão não linear
  • A ideia consiste em calcular um novo espaço de atributos
    • Já fizemos algo parecido quando usamos polinômios a partir do conjunto original de atributos
  • Kernels são uma outra maneira de fazer isso

Kernel gaussiano

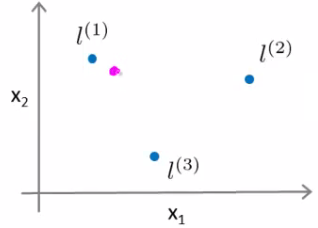
  • Considere que temos 3 pontos de referencia l1l^1, l2l^2 e l3l^3

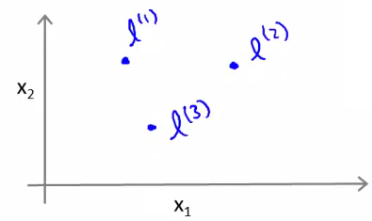
Kernel gaussiano

  • Vamos agora definir 3 novos atributos f1f^1, f2f^2 e f3f^3 com base em l1l^1, l2l^2 e l3l^3 tal que:
    fi=exp⁡(−∥x−li∥2σ2)f^i = \exp \left( - \frac{\lVert x - l^i\rVert}{2 \sigma^2}\right)

  • Essa função de similiradade é chamada de kernel gaussiano

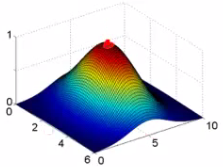
Influência de sigma

  • Sigma controla a "influência" da função de similaridade no espaço

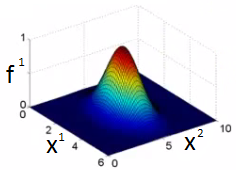
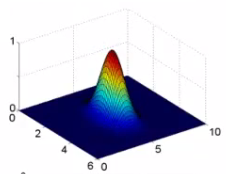
Hipótese

  • Como essa funções influenciam na hipótese?
  • Vamos supor que σ=[−0.5,1,1,0]\sigma = [-0.5, 1, 1, 0]

Hipótese

h:=θ0+θ1f1+θ2f2+θ3f3≥0h := \theta_0 + \theta_1 f_1 + \theta_2 f_2 + \theta_3 f_3 \geq 0

−0.5+1+0+0=0.5-0.5 + 1 + 0 + 0 = 0.5

magenta é classificado como 1

−0.5+0+0+0=−0.5-0.5 + 0 + 0 + 0 = - 0.5

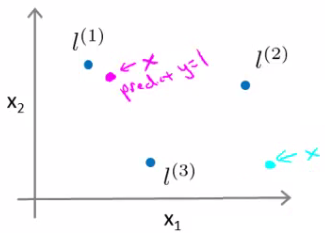
verde é classificado como 0

Hipótese

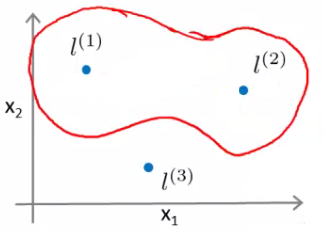
  • Dentro da região marcada como vermelho é classificado como 1
  • Fora é classificado como 0

Kernels

  • Podemos usar cada exemplo do conjunto de treinamento como um ponto de referência
  • Cada novo atributo mede o quão próximo um novo exemplo está dos pontos do conjunto de treinamento
  • Podemos usar SVM para aprender os valores de θ\theta associados a cada novo atributo

Kernels

  • Isso nos leva a nova função de custo

min⁡θC∑im−yicost1(hθ(fi))−(1−yi)cost0(1−hθ(fi))+12∑j=1mθ2\min_{\theta} C \sum_i^m - y^i cost_1 (h_\theta(f^i)) - (1- y_i)cost_0 (1-h_\theta(f^i)) + \frac{1}{2} \sum_{j=1}^m\theta^2

  • O calculo de θ2\theta^2 é normalmente implementado como θ⊺θ\theta^\intercal\theta
    • Isso permite usar alguns truques como θ⊺Mθ\theta^\intercal M \theta
    • MM depende do kernel
    • Calcula uma variação desse termo de maneira mais eficiente

SVM com kernel gaussiano

  • Parâmetro CC da SVM

    • CC grande leva a uma hipótese com baixo bias/alta variância: overfitting
    • CC pequeno leva a uma hipótese com alto bias/baixa variância: underfitting

  • Parâmetro σ2\sigma^2 do Kernel

    • σ2\sigma^2 grande - os atributos variam mais suavemente - alto bias, baixa variância
    • σ2\sigma^2 pequeno - os atributos variam mais abruptamente - baixo bias, alta variância

Outros Kernels

  • Linear (não usar kernel)
  • Polinomial (parecido com a ideia de usar polinômios de maior grau)
  • String
  • X2\Chi^2
  • Intersecção de histograma

Cada um tem um conjunto própio de parâmetros

implementação

  • Não é trivial implementar (não podemos usar a minização do gradiente diretamente)
  • Diversos pacotes provêem implementações eficientes
    • Multiplos Kernels
    • Variações multiclasse
    • Diferentes abordagens de otimização