---
presentation
theme: beige.css
slideNumber: true
width: 1024 height: 768
---
## Aprendizado de Máquina
### Máquinas de vetores de suporte (SVM's)
### Prof. Ronaldo Cristiano Prati
[ronaldo.prati@ufabc.edu.br](mailto:ronaldo.prati@ufabc.edu.br)
Bloco A, sala 513-2
## SVM's
- Máquinas de vetores de suporte são uma outra família de algoritmos de aprendizado de máquina supervisionado
- Em certos casos, é mais simples de usar que redes neurais
- Também tem ótimo desempenho em certas aplicações
## Função de custo
- Relembramos da função de custo da regressão logística:
$$ J(\theta) = \frac{1}{m} \sum_i^m - y^i \log (h_\theta(x^i)) - (1- y_i)\log (1-h_\theta(x^i)) +
\frac{\lambda}{2m} \sum_{j=1}^n\theta^2 $$
- Na regressão logística queremos:
- se $y=1$, $h_\theta(x)\approx 1 $ e $\theta^\intercal x > 0 $
- se $y=0$, $h_\theta(x)\approx 0 $ e $\theta^\intercal x < 0 $
## Função de custo
### Quando $y=1$
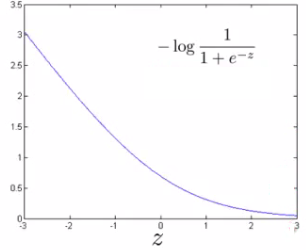
### Quando $y=0$

## Função de custo - SVM
### Quando $y=1$
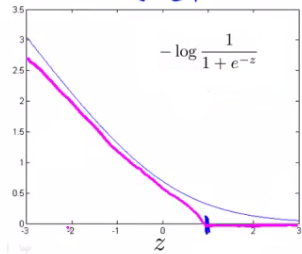
$cost_1(z) $
### Quando $y=0$

$cost_0(z)$
### Função de custo completa - SVM
- Removemos $\frac{1}{m}$ (convenção, não altera o mínimo)
- Parâmetro de regularização associado ao primeiro termo (razão mais adiante)
$$ \min_{\theta} C \sum_i^m - y^i cost_1 (h_\theta(x^i)) - (1- y_i) cost_0 (1-h_\theta(x^i)) + \frac{1}{2}
\sum_{j=1}^n\theta^2 $$
### Função de custo completa - SVM
- O parâmetro $C$ pode é equivalente a $\frac{1}{\lambda}$.
- Se quisermos regulizarar mais (reduzir overfitting), decrescemos $C$
- Se quisermos regularizar menos (reduzir underfitting), aumentados $C$
- Ao contrário da regressão logística, a saída de $h_\theta(x)$ é somente 0 ou 1 (não uma probabilidade)
### Maximização da margem
- SVM também é conhecida como **classificador de margem larga**
- Em SVM queremos:
- se $y=1$, $\theta^\intercal x \geq 1 $ (não apenas $>0$)
- se $y=0$, $\theta^\intercal x \leq -1 $ (não apenas $<0$)
### Maximização da margem
- Para entender o efeito, vamos considerar um valor de $C$ muito grande
- Nesse caso $\sum\theta^2$ predomina na função de custo, que resulta no problema
$$
\begin{aligned}
\min_\theta & \frac{1}{2} \sum_i^n \theta^2\\
s.a. & \theta^\intercal x \geq 1 \text{ se } y=1 \\
& \theta^\intercal x \leq -1 \text{ se } y=0 \\
\end{aligned}
$$
### Maximização da margem
- Esse problema corresponde a encontrar a fronteira de decisão que maximiza a margem de separação entre as classes
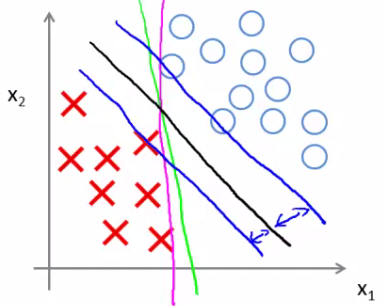
### Maximização da margem
- O parâmetro de regularização $C$ ajuda a contornar *outliers*
$C$ adequado
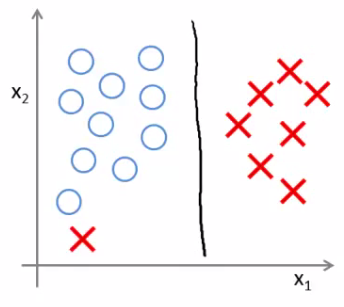
$C$ muito grande
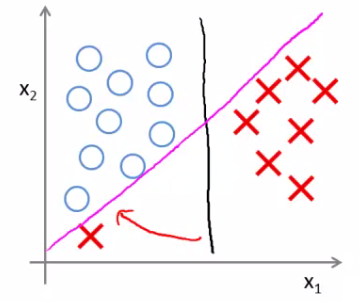
### Maximização da margem
- Por que a margem é maximizada?
- Vamos analisar intuitivamente
- Vamos considerar um problema com 2 dimensões (é mais fácil desenhar)
- Vamos desconsiderar $\theta_0$ por hora
- Vamos considerar também um problema linearmente separável
### Maximização da margem
- Relembre que queremos $\min_\theta \frac{1}{2} \sum_i^n \theta^2$
- Vamos reescrever $\sum_i^n \theta^2$:
$$
\begin{aligned}
\sum \theta^2 & = (\theta_1^2 +\theta_2^2)\\
& = \left(\sqrt{\theta_1 +\theta_2}\right)^2\\
& = \lVert\theta\rVert^2
\end{aligned}
$$
- em que $\lVert\theta\rVert^2$ é a norma (tamanho) do vetor
### Maximização da margem
- O que $\theta^\intercal x$ faz?
$$
\begin{aligned}
\theta^\intercal x^i &=
\begin{bmatrix}
\theta_1\\
\theta_2
\end{bmatrix}
[x_1^i x_2^i] \\
& = \theta_1 x_1 + \theta_2 x_2 \\
& = \langle \theta,x^i\rangle \\
& = p^i\lVert\theta\rVert
\end{aligned}
$$
- em que $\langle \theta,x^i\rangle$ é o produto interno entre $\theta$ e $x^i$, e $p^i$ é o comprimento da projeção de $x^i$ em $\theta$.
### Maximização da margem
- As restrições
$$
\theta^\intercal x \geq 1 \text{ se } y=1 \\
\theta^\intercal x \leq -1 \text{ se } y=0
$$
podem ser reinterpretadas como
$$
p^i\lVert\theta\rVert \geq 1 \text{ se } y=1 \\
p^i\lVert\theta\rVert \leq -1 \text{ se } y=0
$$
### Maximização da margem
- Se a margem entre as classes for pequena
Margem pequena
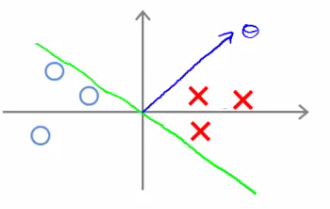
Projeção pequena
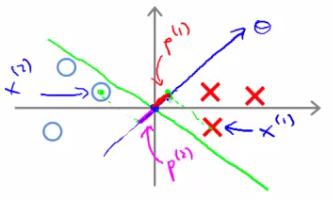
### Maximização da margem
- Se a margem entre as classes for grande
Margem grande
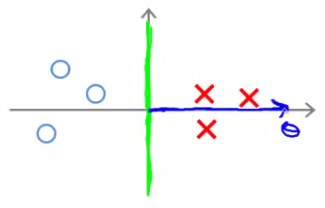
Projeção maximizada
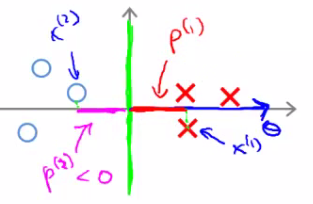
### Maximização da margem
- Se $p$ é pequeno, $\lVert\theta\rVert$ tem que ser grande para garantir as restrições.
- Mas queremos minimizar $\lVert\theta\rVert^2$!
- Maximizar $p$ minimiza $\lVert\theta\rVert$
### Maximização da margem
- Inicialmente ignoramos $\theta_0$
- A fronteira de decisão deve passar obrigatóriamente pela origem
- Se $\theta_0$ puder assumir outros valores, não temos a restrição da fronteira de decisão passar pela origem
- Os princípios gerais continuam os mesmos
## Kernel
- O **kernel** é útil quando queremos computar uma fronteira de decisão não linear
- A ideia consiste em calcular um novo espaço de atributos
- Já fizemos algo parecido quando usamos polinômios a partir do conjunto original de atributos
- Kernels são uma outra maneira de fazer isso
### Kernel gaussiano
- Considere que temos 3 pontos de referencia $l^1$, $l^2$ e $l^3$
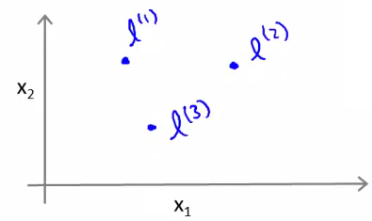
### Kernel gaussiano
- Vamos agora definir 3 novos atributos $f^1$, $f^2$ e $f^3$ com base em $l^1$, $l^2$ e $l^3$ tal que:
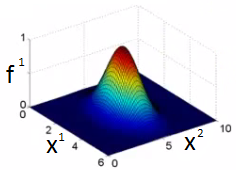
$$ f^i = \exp \left( - \frac{\lVert x - l^i\rVert}{2 \sigma^2}\right)$$
- Essa função de similiradade é chamada de *kernel gaussiano*
### Influência de sigma
- Sigma controla a "influência" da função de similaridade no espaço
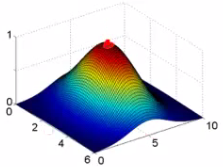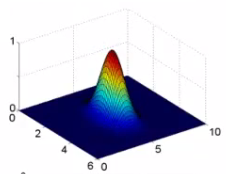
### Hipótese
- Como essa funções influenciam na hipótese?
- Vamos supor que $\sigma = [-0.5, 1, 1, 0]$
### Hipótese
$$ h := \theta_0 + \theta_1 f_1 + \theta_2 f_2 + \theta_3 f_3 \geq 0 $$
$-0.5 + 1 + 0 + 0 = 0.5$
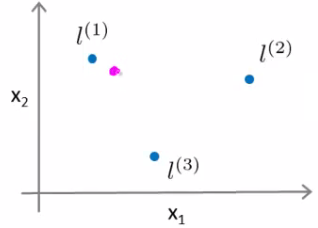
magenta é classificado como 1
$-0.5 + 0 + 0 + 0 = - 0.5$
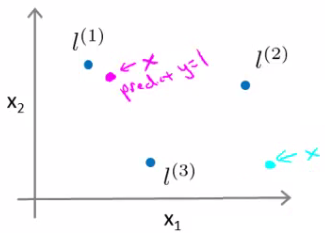
verde é classificado como 0
### Hipótese
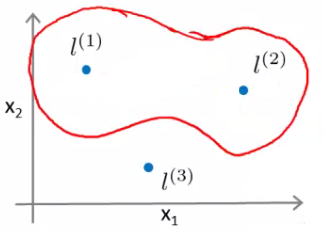
- Dentro da região marcada como vermelho é classificado como 1
- Fora é classificado como 0
## Kernels
- Podemos usar cada exemplo do conjunto de treinamento como um ponto de referência
- Cada novo atributo mede o quão próximo um novo exemplo está dos pontos do conjunto de treinamento
- Podemos usar SVM para aprender os valores de $\theta$ associados a cada novo atributo
## Kernels
- Isso nos leva a nova função de custo
$$ \min_{\theta} C \sum_i^m - y^i cost_1 (h_\theta(f^i)) - (1- y_i)cost_0 (1-h_\theta(f^i)) + \frac{1}{2}
\sum_{j=1}^m\theta^2 $$
- O calculo de $\theta^2$ é normalmente implementado como $\theta^\intercal\theta$
- Isso permite usar alguns truques como $\theta^\intercal M \theta$
- $M$ depende do kernel
- Calcula uma variação desse termo de maneira mais eficiente
## SVM com kernel gaussiano
- Parâmetro $C$ da SVM
- $C$ grande leva a uma hipótese com baixo bias/alta variância: overfitting
- $C$ pequeno leva a uma hipótese com alto bias/baixa variância: underfitting
- Parâmetro $\sigma^2$ do Kernel
- $\sigma^2$ grande - os atributos variam mais suavemente - alto bias, baixa variância
- $\sigma^2$ pequeno - os atributos variam mais abruptamente - baixo bias, alta variância
## Outros Kernels
- Linear (não usar kernel)
- Polinomial (parecido com a ideia de usar polinômios de maior grau)
- String
- $\Chi^2$
- Intersecção de histograma
Cada um tem um conjunto própio de parâmetros
## implementação
- Não é trivial implementar (não podemos usar a minização do gradiente diretamente)
- Diversos pacotes provêem implementações eficientes
- Multiplos Kernels
- Variações multiclasse
- Diferentes abordagens de otimização