Aprendizado de Máquina

Dicas práticas

Prof. Ronaldo Cristiano Prati

ronaldo.prati@ufabc.edu.br

Bloco A, sala 513-2

Pacotes

import matplotlib.pyplot as plt
# data sets
from sklearn.datasets import load_digits, load_iris
# Algoritmos
from sklearn.linear_model import LogisticRegression
from sklearn.svm import SVC
from sklearn.model_selection import learning_curve,
    validation_curve
import numpy as np

Curva de Aprendizado

# Seleciona 2 classes do dataset digits
X,y = load_digits(n_class=2,return_X_y=True)

# cria uma lista de 0.1 a 1, contendo 10 pontos igualmente espaçados
sizes = np.linspace(0.1,1,10)

algs = {
'Logistic Regression' : LogisticRegression(solver='lbfgs'),
'SVM - Gaussian' : SVC()}

for name, alg in algs.items():
    train_sizes, train_scores, test_scores = learning_curve(
        alg, X, y, cv=3, train_sizes=sizes)
    plot_learning_curve(train_sizes, train_scores,
              test_scores,name)

Curva de Aprendizado

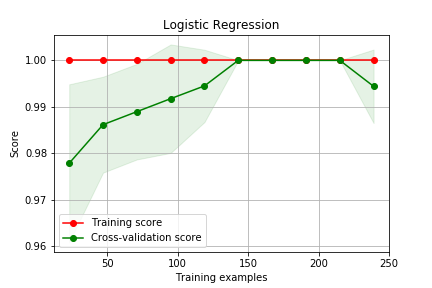
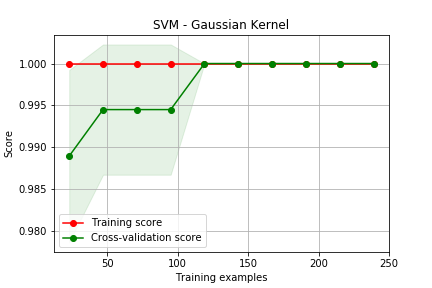
Curva de Validação

X,y = load_digits(return_X_y=True)

# cria pontos exponencialmente expaçados 10^-6 até 10^-1
param_range = np.logspace(-6, -1, 5)

train_scores, test_scores = validation_curve(
    SVC(), X, y, param_name="gamma", param_range=param_range,
    cv=5, scoring="accuracy", n_jobs=1)

Curva de Validação

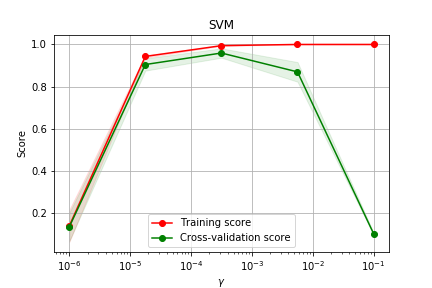
Grid Search

• Em algumas situações queremos variar mais de um parâmetro livre do algoritmo.

  • Em SVMs por exemplo, podemos querer ajustar o parâmetro de regularização $C$ e o parâmetro do kernel $\sigma$

• GridSearch faz uma busca combinando todas as possibilidades para esses valores

Grid Search

X, y = load_iris(return_X_y=True)
# faixa de valores de C
C_range = np.logspace(-2, 10, 13)
# faixa de valores de gamma
gamma_range = np.logspace(-9, 3, 13)
param_grid = dict(gamma=gamma_range, C=C_range)
cv = StratifiedShuffleSplit(y, n_iter=5, test_size=0.2)
grid = GridSearchCV(SVC(), param_grid=param_grid, cv=cv)
grid.fit(X, y)

Grid Search

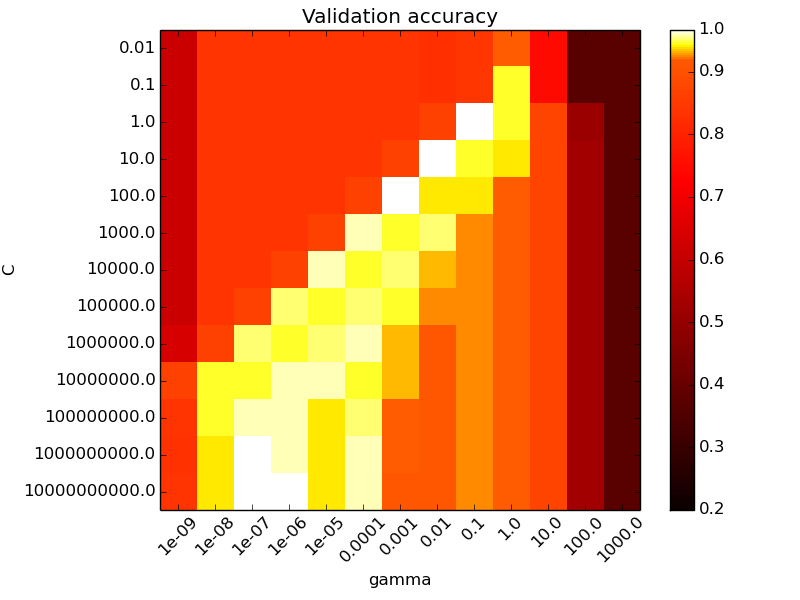
The best parameters are {'C': 1.0, 'gamma': 0.1} with a score of 0.97

Grid Search

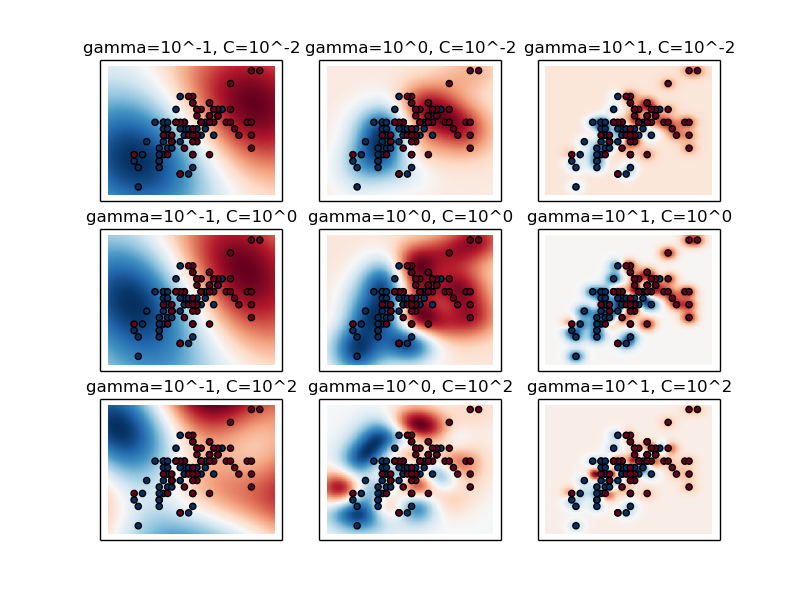
Validação cruzada

• Como visto anteriormente, em validação cruzada, dividimos o conjunto em diferentes partes de treino e teste
• Se a base estiver de alguma maneira ordenada, temos que tomar cuidado em como fazemos a divisão

Validação cruzada

• O Sklearn tem vários metodos que auxiliam a fazer validação cruzada.
• O mais simples deles divide os as linhas da base em blocos igualmente espaçados.

Validação cruzada

from sklearn.model_selection import KFold
from sklearn.metrics import accuracy_score

X, y = load_iris(return_X_y=True)
alg =  LogisticRegression(solver='lbfgs',multi_class='ovr')
accuracies = []
kf = KFold(n_splits=5)
for train, test in kf.split(X):
    X_train = X[train]
    X_test  = X[test]
    y_train = y[train]
    y_test  = y[test]
    alg.fit(X_train,y_train)
    pred = alg.predict(X_test)
    accuracies.append(accuracy_score(y_test,pred))

Validação cruzada

print(accuracies)
[1.0, 0.9, 0.5, 0.9333333333333333, 0.6333333333333333]    
print (np.mean(accuracies),np.std(accuracies))
0.7933333333333332 0.19252705437591536

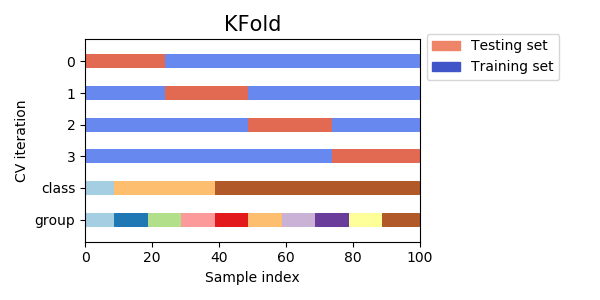
Validação cruzada estratificada

• Esse grande variação vem do fato que, ao fazermos a validação cruzada, pegamos blocos contíguos
• Como a base está agrupada por classes, temos conjuntos com classes não representadas no treino/teste
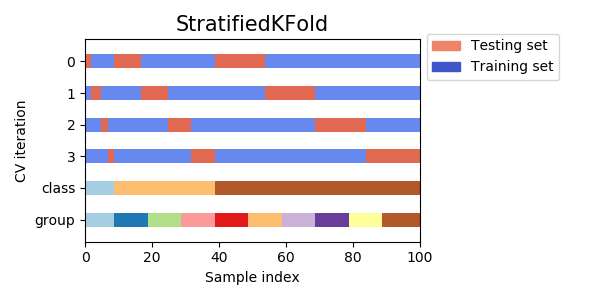
• Validação cruzada estratificada leva em consideração as classes para fazer a divisão

Validação cruzada estratificada

from sklearn.model_selection import StratifiedKFold
from sklearn.metrics import accuracy_score

X, y = load_iris(return_X_y=True)
alg =  LogisticRegression(solver='lbfgs',multi_class='ovr')
accuracies = []
kf = StratifiedKFold(n_splits=5)
for train, test in kf.split(X,y):
    X_train = X[train]
    X_test  = X[test]
    y_train = y[train]
    y_test  = y[test]
    alg.fit(X_train,y_train)
    pred = alg.predict(X_test)
    accuracies.append(accuracy_score(y_test,pred))

Validação cruzada estratificada

print(accuracies)
[0.8666666666666667, 0.9666666666666667, 0.9333333333333333,
 0.9333333333333333, 1.0]
print (np.mean(accuracies),np.std(accuracies))
0.9400000000000001 0.044221663871405324

Validação cruzada agrupada

• Em algumas situações, a base de dados também pode estar organizada em grupos
  • Por exemplo, uma prática comum em classificação de imagens, por exemplo, é rotacionar a imagem em $90^o, 180^o, 270^o$ e $360^o$
  • Nesse caso, para cada imagem inicial, temos outras 4
• Para esses casos, devemos usar validação cruzada agrupada

Validação cruzada agrupada

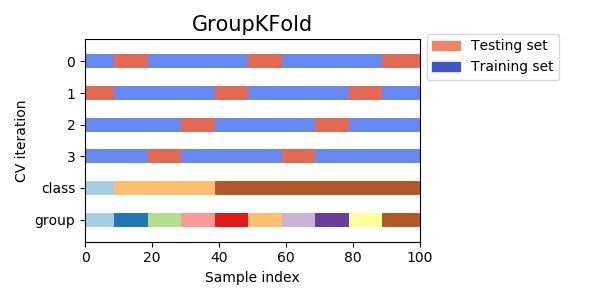
from sklearn.model_selection import GroupKFold

X = [0.1, 0.2, 2.2, 2.4, 2.3, 4.55, 5.8, 8.8, 9, 10]
y = ["a", "b", "b", "b", "c", "c", "c", "d", "d", "d"]
groups = [1, 1, 1, 2, 2, 2, 3, 3, 3, 3]

gkf = GroupKFold(n_splits=3)
for train, test in gkf.split(X, y, groups=groups):
    print("%s %s" % (train, test))
[0 1 2 3 4 5] [6 7 8 9]
[0 1 2 6 7 8 9] [3 4 5]
[3 4 5 6 7 8 9] [0 1 2]

Validação cruzada agrupada

Métrica de avaliação

• Em diversas aplicações, a escolha da métrica de avaliação pode levar a resultados incosistentes
• Por exemplo, quando temos classes desbalanceadas, é fácil ter uma alta acurácia
  • Vamos assumir que fraude de cartão só ocorre 0.1% das transações
  • Classificador que nunca preve fraude acerta 99.9% das vezes!

Matriz de confusão

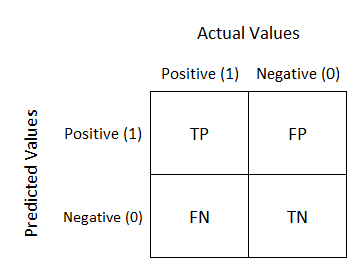
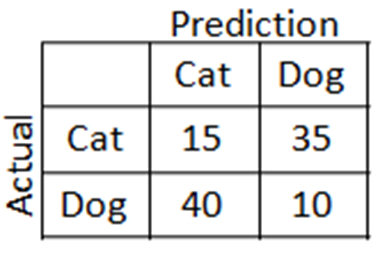
Precisão (precision)

• Avalia cada classe individualmente

• Vamos chamar a nossa classe de interesse positiva

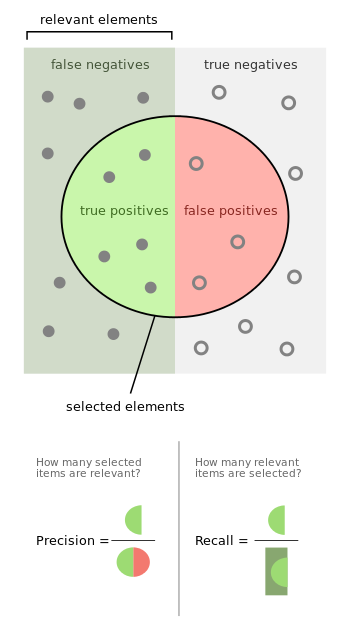
  • Quando o algoritmo prediz um exemplo como positivo, com que frequência ele acerta aquela predição?

  $precision = \frac{TP}{TP+FP}$

Revocação (recall)

• Avalia cada classe individualmente

• Vamos chamar a nossa classe de interesse positiva

  • Com relação a todos os exemplos positivos do conjunto de teste, quantos o algoritmo acertou?

  $recall = \frac{TP}{TP+FN}$

Métrica de avaliação

• Geralmente escolhemos a classe minoritária como a de interesse
  • Doença rara, fraude, etc.
• Calcular precisão e revocação para essa classe nos dá uma ideia melhor do desempenho do algoritmo para aquela classe
• Eventualmente podemos computar para outra(s) classe(s) também

F1-measure

• A medida $F1$ é muito usada em algumas áreas como um compromisso entre precisão e revocação.
• Média harmônica entre precisão e revocação

$F1 = 2 \cdot \frac{precision*recall}{precision + recall}$

Trade-off entre precisão e revocação

• Para muitas aplicações, queremos controlar o trade-off entre precisão e revocação
• É fácil otimizar um ou outro:
  • precisão: só predizar o mais seguro (e.g., o de maior probabilidade)
  • revocação: predizer todos os exemplos como positivos
• Entretanto, otimizar os dois pode ser difícil

Trade-off entre precisão e revocação

• Uma maneira de controlar o trade-off entre essas duas medidas é variar o limiar da fronteira de decisão
• Por exemplo, na regressão logística, o algoritmo dá como saída a probabilidade da classe

Trade-off entre precisão e revocação

• Normalmente assumimos que a fronteira está em predizer classe positiva se $h_\theta(x) > 0.5$.
  • Por exemplo, podemos aumentar precisão predizendo positivo se $h_\theta(x) > 0.8$;
  • ou aumentar a revocação predizendo positivo se $h_\theta(x) > 0.2$

Trade-off entre precisão e revocação

• A escolha do limiar é dependente do problema
• Podemos analisar o desempenho de um modelo considerando todos os possíves limiares
  • Curva precisão-revocação (precision-recall)
  • Precision (eixo $y$)
  • Recall (eixo $x$)
  • Para cada possível limiar, calcula-se um valor de precision e recall

Precison-recall curve

from sklearn.metrics import precision_recall_curve
from sklearn.model_selection import train_test_split
from sklearn.datasets import make_classification
from sklearn import svm

X,y = make_classification(class_sep=0.5)

X_train, X_test, y_train, y_test =
 train_test_split(X, y,test_size=.5)

alg = svm.LinearSVC()
alg.fit(X_train, y_train)
y_score = alg.decision_function(X_test)
precision, recall, t = precision_recall_curve(y_test, y_score)

Precision recall curve