Aprendizado de Máquina

Aprendizado não-supervisionado (agrupamento)

Prof. Ronaldo Cristiano Prati

ronaldo.prati@ufabc.edu.br

Bloco A, sala 513-2

Tipos de Aprendizado

• Supervisionado os exemplos tem um atributo de interesse pré-determinado
• Não supervisionado não temos um atributo de interesse pré-determinado

Aprendizado não supervisionado

• Agrupamento identificar alguma estrutura nos dados
• Redução de dimensionalidade usar características estruturais para simplificar os dados

Agrupamento

• Organizar dados em grupos de forma que exista

  • uma alta similaridade intra-classe
  • uma baixa similaridade inter-classes

• Mais informalmente, encontrar grupos que ocorrem naturalmente entre objetos.

Qual é o agrupamento natural desses objetos?

Agrupamento é subjetivo

Aprupamento particional

• Algoritmos Particionais: Construir diversas partições de acordo com algum critério

Aprupamento hierárquico

• Algoritmos Hierárquicos: Criar uma decomposição hierárquica de um conjunto de objetos utilizando algum critério

K-médias

• Algoritmo particional: cada ponto é associado a um único grupo
• Precisamos decidir antecipadamente o número $k$ de grupos

K-médias - algoritmo

1. Decidir um valor para k.
2. Inicializar os centros dos k grupos (aleatoriamente, se necessário).
3. Decidir o grupo dos N objetos por meio da associação ao centro do grupo mais próximo.
4. Re-estimar os centros dos k grupos, assumindo que a associação com os grupos encontradas anteriormente está correta.
5. Se nenhum dos N objetos mudou de grupo na última iteração, pare. Caso contrário, volte para o passo 3.

K-médias - exemplo

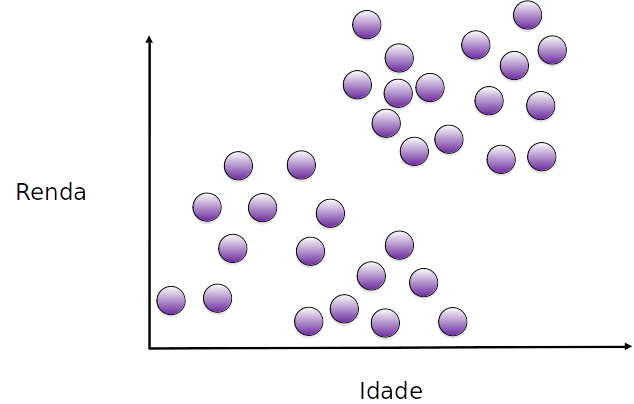
queremos encontrar 2 grupos

K-médias - exemplo

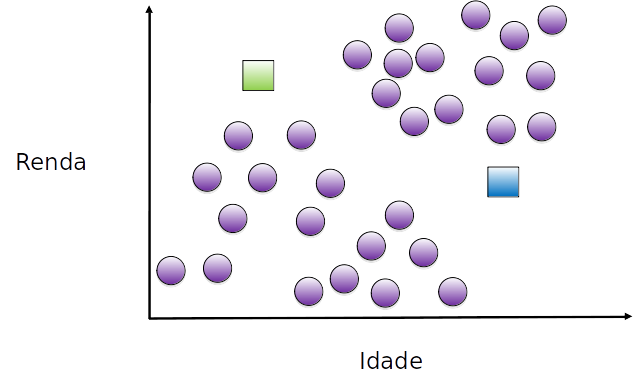
inicalizamos aleatoriamente o centróide dos dois grupos

K-médias - exemplo

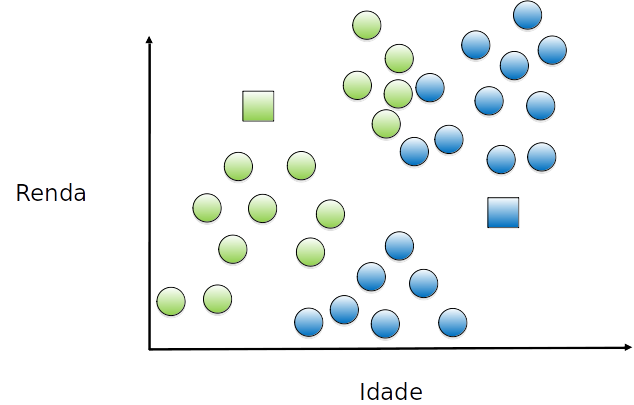
Cada exemplo é atribuído a um grupo, de acordo com o centróide mais próximo

K-médias - exemplo

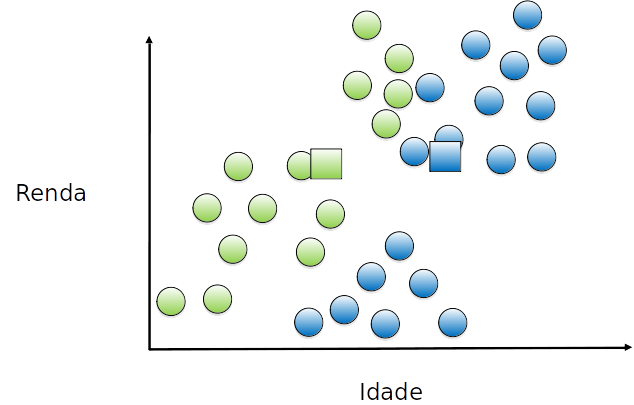
O centróide do grupo é movido para o centro de cada grupo

K-médias - exemplo

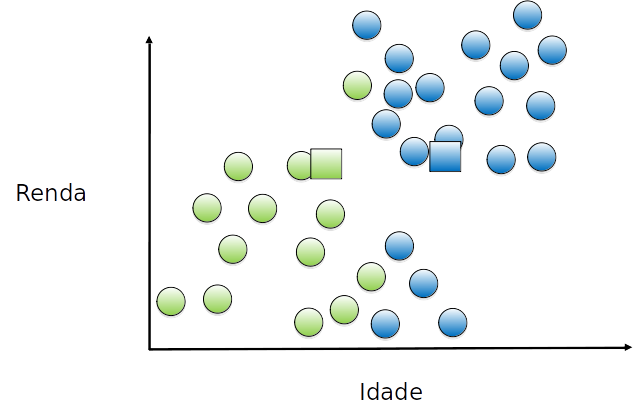
Cada exemplo é (re)atribuído a um grupo, de acordo com o (novo) centróide mais próximo

K-médias - exemplo

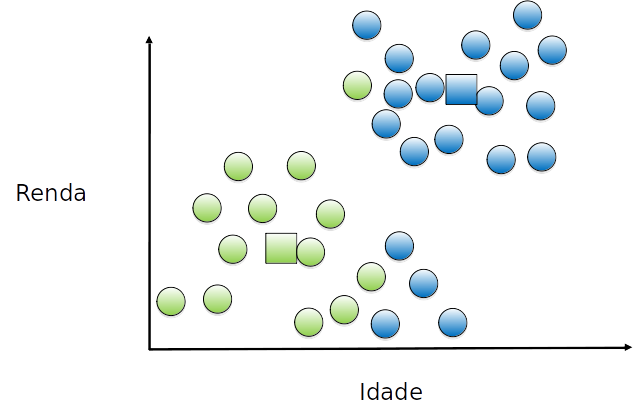
O centróide do grupo é movido (novamente) para o (novo) centro de cada grupo

K-médias - exemplo

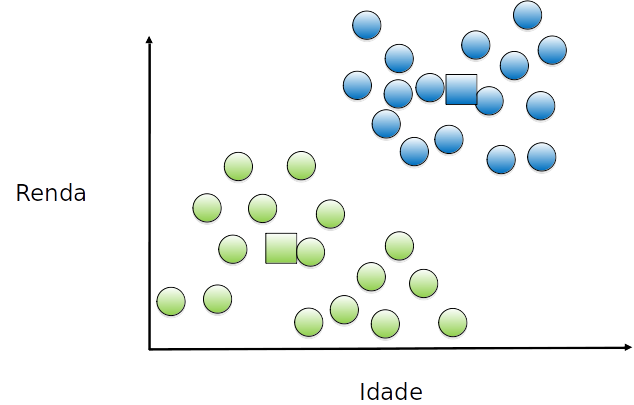
Cada exemplo é (re)atribuído a um grupo, de acordo com o (novo) centróide mais próximo

K-médias - exemplo

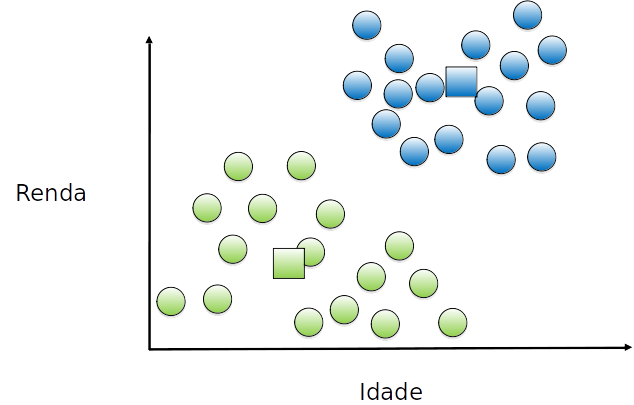
O centróide do grupo é movido (novamente) para o (novo) centro de cada grupo.

K-médias - exemplo

Cada exemplo é (re)atribuído a um grupo, de acordo com o (novo) centróide mais próximo. Como não houve alteração, convergiu.

K-médias

• O k-médias é dependente do número de cluster $k$

• O k-médias é sensível à inicialização dos clusters

K-médias - diferentes execuções

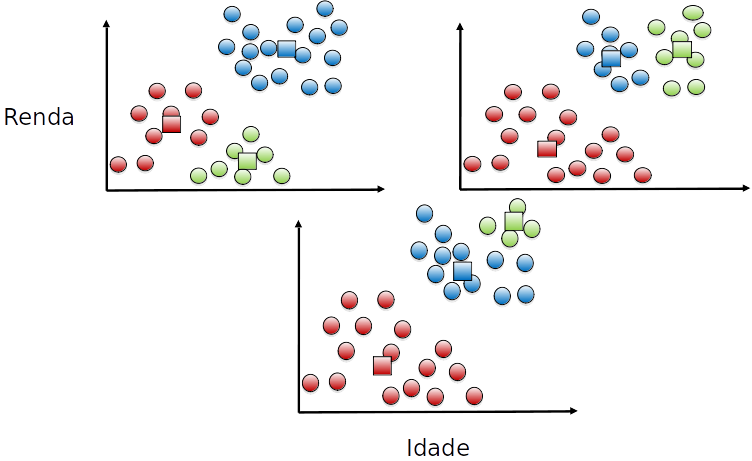
Função objetivo

• Seja $c^i$ o cluster $i$, $\mu_{c^i}$ o centróide do cluster $i$ e $x^i$ um exemplo associado ao cluster $i$. Podemos definir a função objetivo como:

$J(c^1,\dots,c^k,\mu_{c^1},\dots,\mu_{c^k}) = \frac{1}{m} \sum_i^m \| x^i - \mu_{c^i}\|^2$

• Soma dos quadrados da distância de cada ponto ao seu respectivo cluster.
• Também chamado de inércia.

Função objetivo

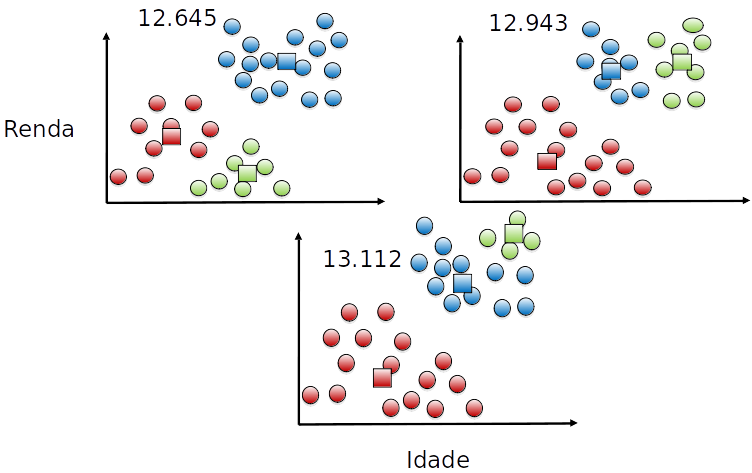
Escolha do valor de $k$

• Alguns problemas tem um valor de $k$ bem definido
  • Agrupar tarefas similares em 4 núcleos de CPU ($k=4$)
  • Agrupar roupas em 5 diferentes tamanhos para cobrir a maioris das pessoas ($k=5$)
  • Agrupar comentários similares em 10 grupos ($k=10$)

Escolha do valor de $k$

• Quando não temos conhecimento do domínio, escolher $k$
• Método do "cotovelo"
  • Executar k-médias para diferentes valores de $k$
  • Fazer um gráfico de $k$ por $J$
  • Escolher $k$ em que $J$ se "estabiliza"

Escolha do valor de $k$

• Chama-se método do "cotovelo" pois espera-se que o gráfico tenha o formato de um braço dobrado, e o $k$ adequado seria o "cotovelo"

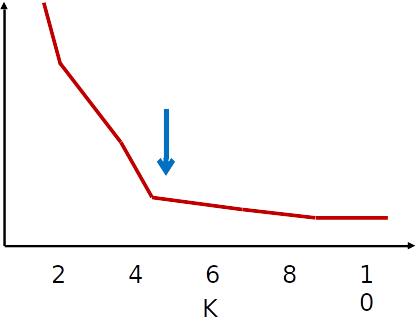
• Nem sempre tem esse formato

Suposições

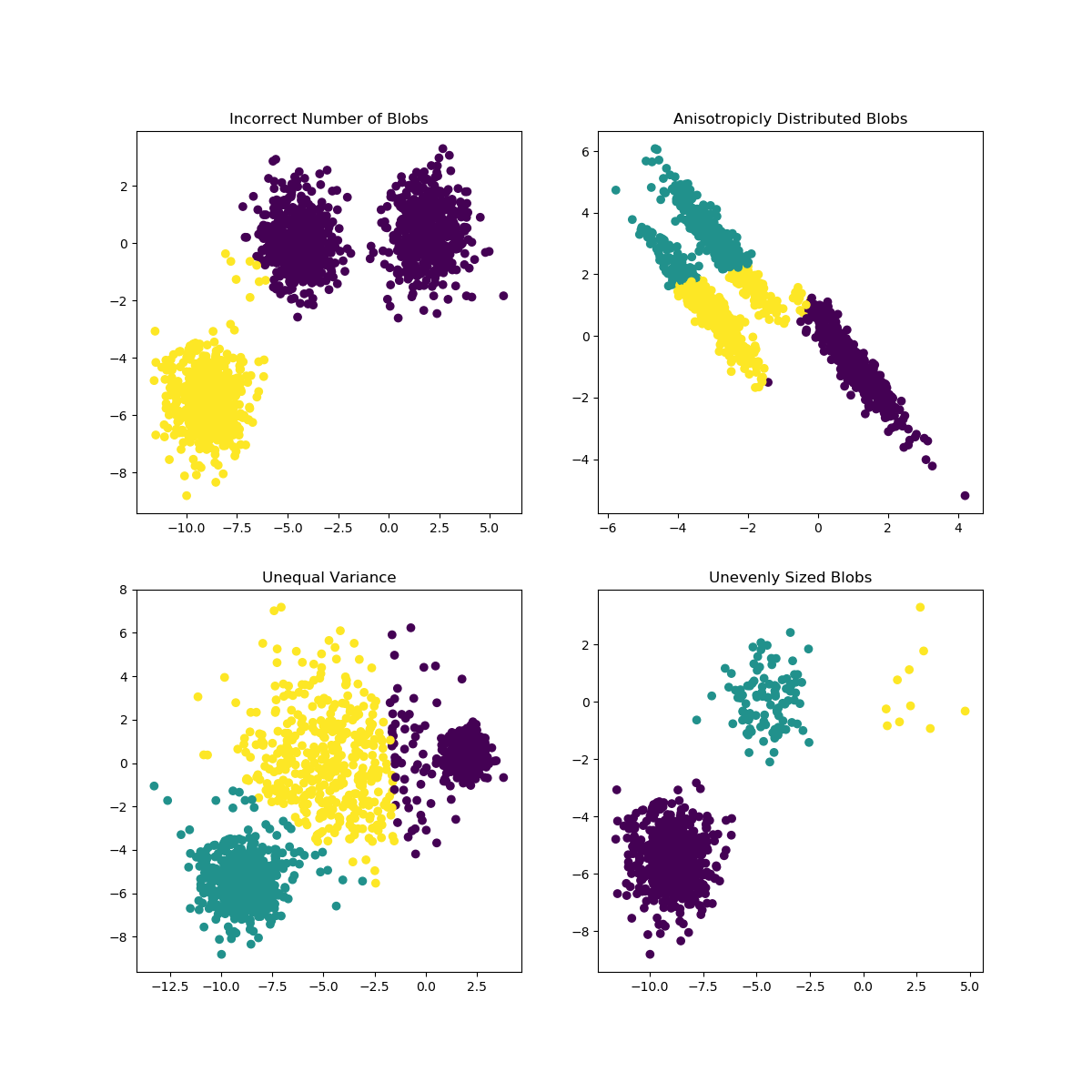
Escolha da medida de distância

• A escolha da medida de distância é extremamente importante para o sucesso do agrupamento
• Cada métrica tem vantagens/desvantagens e casos de uso mais apropriado
• Muitas vezes é preciso realizar uma avaliação empírica

Distância Euclideana

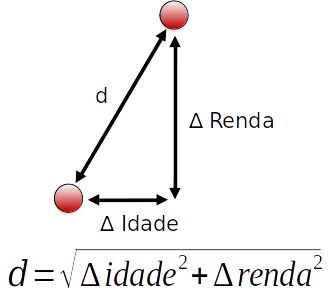
Distância Manhattan

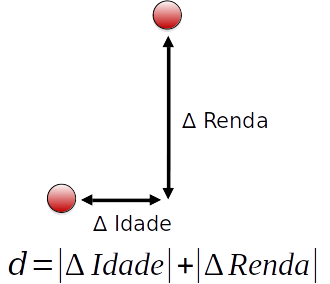
• Menos sensível a outliers

Distância de Cosenos

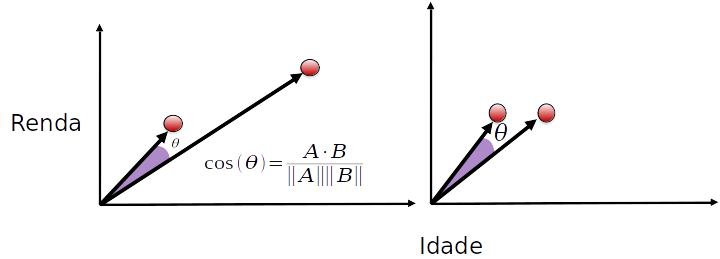
• Menos sensível a escala e dimensionalidade

Agrupamento hierárquico

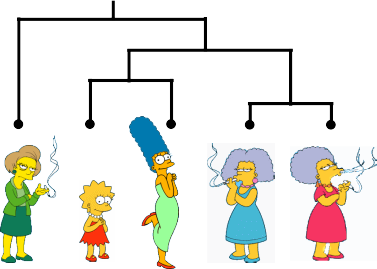
• Representa a similaridade entre os dados por meio de um dendograma

• A similaridade entre dois objetos em um dendograma é representada pela altura do nó interno mais baixo que eles compartilham.

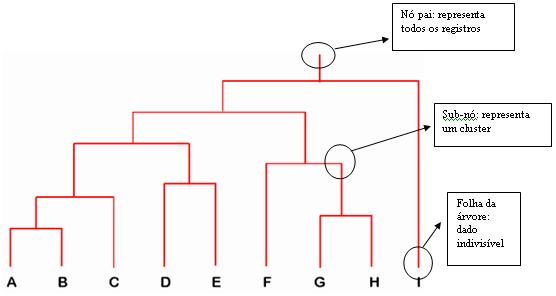
Número de clusters

• O dendograma pode ajudar a determinar o número “correto” de agrupamentos. Nesse caso, a existência de duas árvores bem separadas é um forte indicativo de dois clusters.
• Infelizmente, raramente as coisas são assim tão claras.

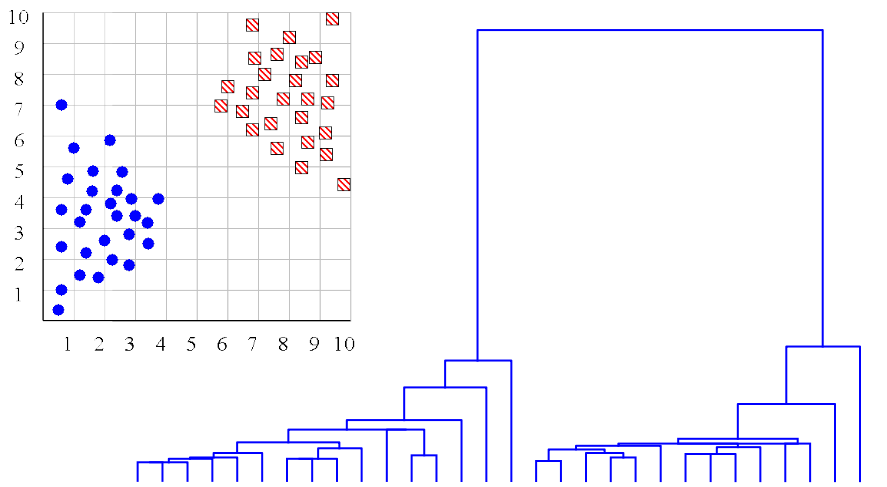
outliers

• Um possível uso de dendogramas é a detecção de outliers
• Um ramo único e isolado sugere um dado que é muito diferente de todos os demais

Agrupamento hierárquico

• O número possível de dendogramas cresce exponencialmente com o tamanho do dataset
• Busca heurística:
  • aglomerativo: começa agrupando exemplos individualmente até construir um único cluster
  • divisivo: começa com um único cluster e vai dividindo recursivamente até chegar nos exemplos.

Matriz de Distância

• contém as distâncias entre cada par de objetos da base de dados

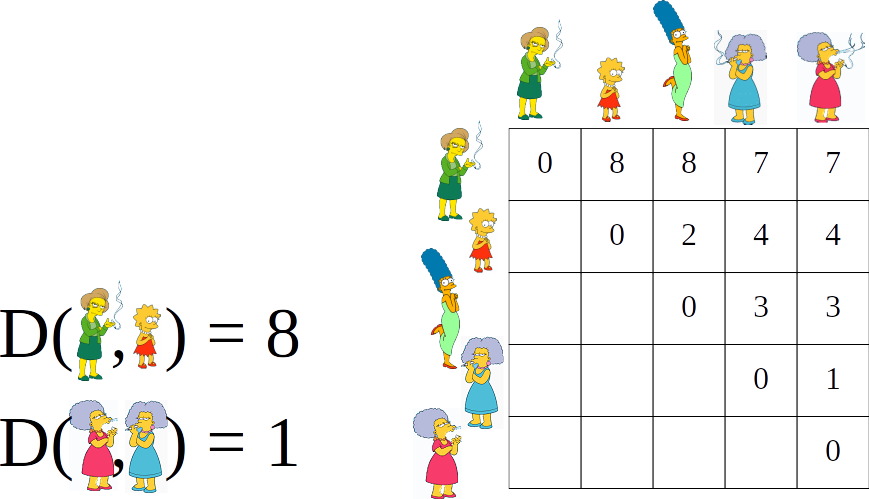
Abordagem aglomerativa

1. Cada exemplo representa um grupo
2. Encontra o melhor par para (menor distância) para criar um novo grupo
3. Recalcula a distânci do grupo criado para os demais
4. Volta ao passo 2. até que um único grupo seja formado

Abordagem aglomerativa

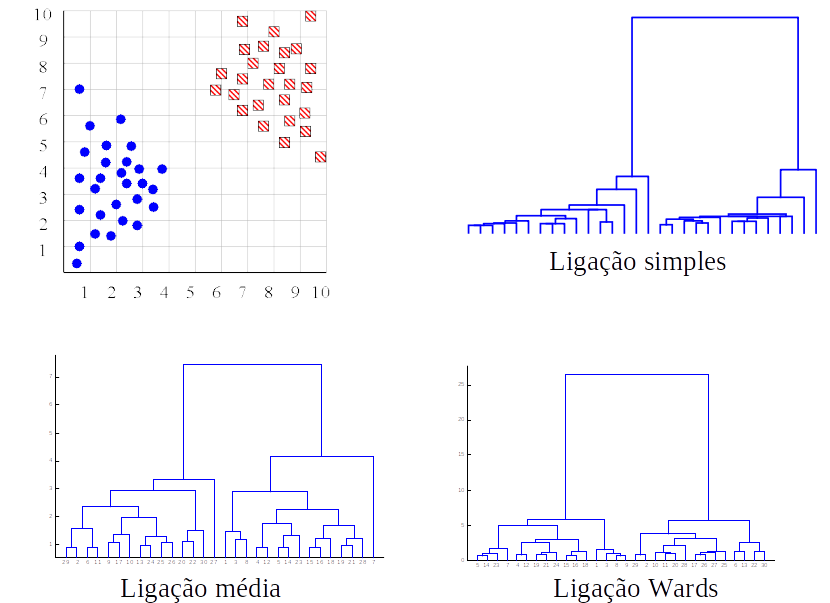
Distância entre clusters

• Ligação simples (vizinho mais próximo): distância entre os dois objetos mais próximos (vizinhos mais próximos) nos diferentes clusters.
• Ligação completa (vizinho mais distante): maior distância entre dois objetos nos diferentes clusters (“vizinhos mais distantes”).
• Ligação média de grupo: distância média entre todos os pares de objetos nos diferentes clusters.
• Ligação Wards: minimiza a variância entre os dois clusters aglomerados.

Distância entre clusters

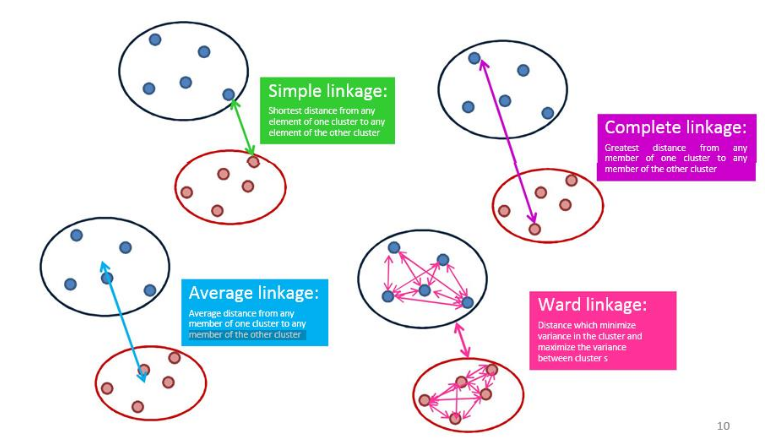
Distância entre clusters

Agrupamento hierárquico

• Não existe a necessidade de especificar o número de clusters a priori.
• A natureza hierárquica é facilmente mapeada pela intuição humana para alguns domínios.
• Eles não escalam bem: a complexidade de tempo é pelo menos $O(n^2)$, na qual $n$ é o número de objetos.
• Como qualquer algoritmo de busca heurística, mínimos locais são um problema.
• A interpretação dos resultados é (muito) subjetiva.