BCM0505-15 - Processamento da Informação

Aula A04 – 06/05: Estatísticas em Vetores

• Momentos: média, variância e desvio padrão.
• Regressão linear em uma variável.
• Heaps e filas de prioridade.

---

Médias Aritméticas: Simples e Ponderada

Problema A4.1: Dada uma lista $A[0\,..n-1]$ com $n\geq 1$ pontos flutuantes, determine a média aritmética simples dos elementos de $A$: $$\mu_A = \mathbb{E}[A] := \frac{1}{n}\sum_{i=0}^{n-1} A[i].$$

Versão baseada em princípios fundamentais:

# devolve a média aritmética simples de A; assume que A tem ao menos um elemento.
def average (A: [float]) -> float:
  assert (len (A) >= 1)
  s = 0.0; for a in A: s += a
  return s / len (A)

Observe que introduzimos a diretiva assert no código acima. Seja $P$ uma expressão lógica codificando um predicado. Se a avaliação de $P$ no momento em que assert (P) é executada resultar em False, a execução do programa é abortada (interrompida com mensagem de erro); se, por outro lado, P == True, a execução prossegue normalmente.
No caso, uma chamada à average com uma lista vazia (len(A) < 1) produziria o efeito (desejado) abaixo:

>>> print (average ([]))
Traceback (most recent call last):
  File "main.py", line 7, in <module>
    print (average ([]))
  File "main.py", line 3, in average
    assert (n >= 1)
AssertionError
>>>

Assertivas (como são chamadas) são artifícios úteis no desenvolvimento e depuração de programas. Para mais informações, veja documentação.

Versão utilizando a função sum:

# devolve a média aritmética simples de A; assume que A tem ao menos um elemento.
def average (A: [float]) -> float:
  assert (len (A) >= 1)
  return sum (A) / len (A)

Python disponibiliza as funçãos mean e fmean no módulo statistics como solução ao Problema A4.1 — possui comportamento semelhante, mas lança exceções em casos de erros.

from statistics import mean
print (mean ([1,2,3,4]))

Problema A4.2: Dadas duas listas $A[0\,..n-1]$ e $w[0\,..n-1]$ com $n\geq 1$ pontos flutuantes, em que $$0\leq w[i]\leq 1 \qquad\text{para todo $i$, e}\qquad \sum_{i=0}^{n-1} w[i] = 1,$$ determine a média aritmética ponderada dos elementos de $A$ com relação à $w$: $$\mu_{A\sim w} = \mathbb{E}_{w}[A] := \sum_{i=0}^{n-1} w[i]*A[i].$$

Claramente, o Problema A4.1 é um caso particular deste, já que basta tomar $w[i]=1/n$ para reduzi-lo ao A4.2.
A qualificação ponderada advém dos valores em $w$ funcionarem como “pesos” para os elementos em $A$.
Observe que o fato de requerermos $0\leq w[i]\leq 1$ não é severamente restritivo.

Versão baseada em princípios fundamentais:

# devolve a média aritmética ponderada de A com relação à w; assume que A e w têm ao menos um elemento.
def weighted_average (A: [float], w: [float]) -> float:
  n, s = len (A), 0.0
  assert (n >= 1)
  for i in range (n): s += w[i] * A[i]
  return s

Versão utilizando gerador, sum e zip:

# devolve a média aritmética ponderada de A com relação à w; assume que A e w têm ao menos um elemento.
def weighted_average (A: [float], w: [float]) -> float:
  assert (len (A) >= 1)
  return sum (wi * ai for wi, ai in zip (w, A))

---

Momentos

Problema A4.3: Dados um inteiro $m\geq 1$ e duas listas $A[0\,..n-1]$ e $w[0\,..n-1]$ com $n\geq 1$ pontos flutuantes, em que $$0\leq w[i]\leq 1 \qquad\text{para todo $i$, e}\qquad \sum_{i=0}^{n-1} w[i] = 1, \qquad(*)$$ determine o $m$-ésimo momento de $A$ com relação à $w$: $$\mathbb{E}_{w}[A^{m}] := \sum_{i=0}^{n-1} w[i]*\big(A[i]\big)^m.$$

Claramente, o Problema A4.2 é um caso particular deste, quando $m=1$.

def mth_moment (m: int, A: [float], w: [float]) -> float:
  return sum (wi * ai ** m for wi, ai in zip (w, A))

Nota: As relações $(*)$ sobre $w$ induzem uma medida de probabilidade (discreta) para os elementos de $A$. Com efeito, $A$ representa um espaço amostral em que o elemento $A[i]$ tem medida de probabilidade $w[i]$. Abusamos da notação e utilizamos $A$ como uma variável aleatória que toma valores neste espaço.

---

Médias Geométrica e Harmônica

Problema A4.4: Dada uma lista $A[0\,..n-1]$ com $n\geq 1$ pontos flutuantes, determine a média geométrica dos elementos de $A$: $$\nu_A = \left(\prod_{i=0}^{n-1} A[i]\right)^{1/n}.$$

Versão baseada em princípios fundamentais:

# devolve a média geométrica de A; assume que A tem ao menos um elemento.
def geom_mean (A: [float]) -> float:
  assert (len (A) >= 1)
  p = 0.0; for a in A: p *= a
  return p ** (1 / len (A))

Versão utilizando a função prod no módulo math, introduzida no Python 3.8:

from math import prod

# devolve a média geométrica de A; assume que A tem ao menos um elemento.
def geom_mean (A: [float]) -> float:
  assert (len (A) >= 1)
  return prod (A) ** (1 / len (A))

Caso os elementos em $A$ sejam positivos, as relações $e^{\log x} = x$ e $$\log \prod_{i=0}^{n-1} A[i] = \sum_{i=0}^{n-1} \log A[i]$$ permite a escrita do código abaixo:

from math import log, exp

# devolve a média geométrica de A; assume que A tem ao menos um elemento, e que todos são positivos.
def geom_mean (A: [float]) -> float:
  assert (len (A) >= 1)
  return exp (sum (map (log, A))) ** (1 / len (A))

Observe que fizemos uso da função map (f, L), que aplica a função $f$ a cada argumento de um iterável $L$ e devolve o iterável (de mesma natureza) resultante. Por exemplo, se $L=[10, 100, 1000, 10000]$:

>>> from math import log10
>>> print (map (log10, L))
[1, 2, 3, 4]
>>>

Note que a média geométrica é simples o suficiente para que não precisemos recorrer a uma implementação deste tipo. De qualquer forma, é sempre bom ter em mente a transformação acima; ela é de grande utilidade!

Exercício 1: mostre que $\nu_A \leq \mu_A,$ para qualquer $A=[a_0,a_1,\ldots,a_{n-1}]$ com $n\geq 1.$

Problema A4.5: Dada uma lista $A[0\,..n-1]$ com $n\geq 1$ pontos flutuantes não nulos, determine a média harmônica dos elementos de $A$: $$\eta_A = \left(\frac{1}{n}\sum_{i=0}^{n-1} \big(A[i]\big)^{-1}\right)^{-1} = \frac{n}{\frac{1}{A[0]} + \frac{1}{A[1]} + \cdots + \frac{1}{A[n-1]}}.$$

Versão baseada em princípios fundamentais:

# devolve a média harmônica de A; assume que A tem ao menos um elemento, e que todos são diferentes de zero.
def harm_mean (A: [float]) -> float:
  assert (len (A) >= 1)
  s = 0.0; for a in A: s += 1/a
  return len (A) / s

Versão utilizando map e lambda:

# devolve a média harmônica de A; assume que A tem ao menos um elemento, e que todos são diferentes de zero.
def harm_mean (A: [float]) -> float:
  assert (len (A) >= 1)
  return len (A) / sum (map (lambda x: 1/x, A)) 

Nota: a média harmônica é apropriada em situações em que a média de razões (ex: velocidades em km/h) é desejada.

Python disponibiliza as funções geometric_mean e harmonic_mean no módulo statistics.

---

Variância e Desvio Padrão

Problema A4.6: Dadas uma lista não vazia $A[0\,..n-1]$ de pontos flutuantes e uma lista $w[0\,..n-1]$ de pesos entre $0$ e $1$ e tal que $\sum_{i=0}^{n-1} w[i]=1$, determine a variância de $A$ com relação a $w$: $$\sigma_{A\sim w}^2 = \mathbb{E}_{w}[A^2] - \big(\mathbb{E}_{w}[A]\big)^2 = \sum_{i=0}^{n-1} w[i]\cdot A[i]^2 - \left(\sum_{i=0}^{n-1} w[i]\cdot A[i]\right)^2.$$

Versão baseada em princípios fundamentais:

# recebe : uma lista A de reais e uma lista w de pesos entre 0 e 1 tal que `sum (w) == 1`
# devolve: a variância dos elementos em A de acordo com w
def variance (A: [float], w: [float]) -> float:
  assert (len (A) >= 1)
  a = b = 0.0
  for i in range (len (A)):
    b += w[i] * A[i]
    a += b * A[i]
  return a - b*b

Versão com gerador, sum() e zip():

# recebe : uma lista A de reais e uma lista w de pesos entre 0 e 1 tal que `sum (w) == 1`
# devolve: a variância dos elementos em A de acordo com w
def variance (A: [float], w: [float]) -> float:
  assert (len (A) >= 1)
  a = sum (wi*ai*ai for ai, wi in zip (A, w))
  b = sum (wi*ai for ai, wi in zip (A, w))
  return a - b*b

Exercício 2: mostre que $\sigma_{A\sim w}^2\geq 0,$ para qualquer $A=[a_0,a_1,\ldots,a_{n-1}]$ com $n\geq 1.$

O desvio padrão é a raiz quadrada da variância: $\sigma_{A\sim w} = \sqrt{\sigma_{A\sim w}^2}.$

from math import sqrt
def std_deviation (A: [float], W: [float]) -> float:
  return sqrt (variance (A, w))

---

Regressão Linear Simples

Considere o seguinte quadro. Alice, trabalhando em um experimento de medições discretas, observou resultados $y_0,y_1,\ldots,y_{n-1}$ para entradas $x_0,x_1,\ldots,x_{n-1}$. Por exemplo, cada $x_i$ poderia representar um dia e cada $y_i$, a correspondente temperatura em Celsius, medida ao meio-dia no laboratório em que ela trabalha. Como próximo passo, Alice deseja formular uma hipótese que:

• explique os resultados obtidos (pares $(x_i,y_i)$) e,
• permita a previsão de resultados a entradas que não pertençam a $\{x_0,x_1,\ldots,x_{n-1}\}$, extrapolando / generalizando assim o experimento.

Dada a natureza bidimensional dos dados, Alice acredita que um modelo linear simples, com apenas uma variável preditora, consistirá em uma resposta adequada. Na regressão linear simples, dada a variável preditora $x$, a resposta é modelada como $$y=\beta_0+\beta_1x,$$ que descreve uma linha reta com coeficiente angular $\beta_1$ e que intercepta o eixo $y$ em $\beta_0$. O objetivo consiste em determinar os parâmetros desconhecidos $\beta_0$ e $\beta_1$, dados os pontos $(x_i,y_i)$.

Para $n>2$, o sistema é claramente super-determinado — lembre-se que dois pontos determinam uma reta em $\mathbb{R}^2$. Logo, a menos que todos os $n$ pontos tenham sido extraídos da própria reta que buscamos, o problema acima não tem solução.

Restrições tecnológicas que introduzam imprecisões nos resultados e/ou erros de origem mecânica, eletrônica ou humana na obtenção dos mesmos implicam, portanto, que raramente os dados de um experimento se alinharão precisamente a uma hipótese linear. Observe ainda que, em geral, não podemos compensar os fatores de erro, já que estes costumam ser variáveis e indeterminados.

Um possível contorno a esta situação consiste em definir $$r_i=(y_i-\beta_0-\beta_1x_i)$$ como o valor residual do par $(x_i,y_i)$. O objetivo passa a ser, então, a estimativa dos parâmetros não observados $\beta_0$ e $\beta_1$ de forma a tornar os residuais tão pequenos quanto possível. Uma maneira de atingir este objetivo consiste na utilização do método de mínimos quadrados, que determina $\beta_0$ e $\beta_1$ de forma a minimizar a soma dos quadrados dos residuais: $$ \min_{\beta_0,\beta_1} \sum_{i=0}^{n-1} (y_i-\beta_0-\beta_1x_i)^2. $$ O método é bastante simples e, com um pouco de cálculo diferencial, é possível obter a forma fechada que segue: $$ \beta_0 = \overline{y} - \beta_1\overline{x} \qquad\textrm{e}\qquad \beta_1 = \frac{\displaystyle n\sum_{i=0}^{n-1} (x_i-\overline{x})(y_i-\overline{y})} {\displaystyle\sum_{i=0}^{n-1} (x_i-\overline{x})^2}, $$ com $$ \overline{x} = \mathbb{E}[x] := \frac{1}{n}\sum_{i=0}^{n-1} x_i \qquad\textrm{e}\qquad \overline{y} = \mathbb{E}[y] := \frac{1}{n}\sum_{i=0}^{n-1} y_i. $$

Problema A4.7: Dadas duas listas $x[0\,..n-1]$ e $y[0\,..n-1]$, em que $(x[i],y[i])$ representa um ponto amostral, determine as estimativas de $\beta_0$ e $\beta_1$.

def least_squares (x: [float], y: [float]) -> (float, float):
  n = len (x)
  xbar = average (x)
  ybar = average (y)

  cov = var = 0
  for i in range (n):
    cov += (x[i]-xbar)*(y[i]-ybar)
    var += (x[i]-xbar)*(x[i]-xbar)

  beta_1 = n*cov/var
  beta_0 = ybar - beta_1*xbar
  return (beta_0, beta_1)    

Problema A4.8: Escreva uma função que recebe um valor real ${x^}$, $\beta_0$ e $\beta_1$ e devolve o valor ${y^}$, correspondente à predição de ${x^*}$.

def LR_prediction (xstar, beta_0, beta_1):
  return beta_0 + beta_1*xstar

< incluir criação de gráficos >

import matplotlib.pyplot as plt

---

Heaps e Filas de Prioridade

Uma lista $H[1\,..n]$ de valores comparáveis (inteiros, reais, etc.) é um max-heap se $$H[j//2] \geq H[j] \qquad \text{para todo} \qquad 2\leq j\leq n. \qquad (@)$$ Por exemplo: $H_1=[5,2,5,1,1,4,0,1]$ e $H_2=[5,4,3,2,1,0]$ são um max-heaps, mas $H_3=[5,2,3,3,1]$ e $H_4=[1,4,5,2,3,8]$ não o são.
Uma lista vazia e listas unitárias são, trivialmente, max-heaps.

Problema A4.9: Escreva uma função que recebe uma lista $H$ de inteiros e determina se $H$ é um max-heap.

def is_maxheap (H: [int]) -> bool:
  for j in range (len (H), 1, -1):
    if H[j//2] < H[j]: return False
  return True

De forma similar, define-se um min-heap substituindo “$\geq$” por “$\leq$” em $(@)$.
Não é difícil perceber — nem provar — que:

• um elemento máximo em um max-heap $H$ é encontrado em $H[1]$,
• toda sequência decrescente é um max-heap,
• nem todo max-heap é uma sequência decrescente.

Exercício 3: Suponha que $H[1\,..n]$ é um max-heap cujos elementos são dois a dois distintos. Onde pode estar o segundo maior elemento? E o terceiro maior elemento?

É conveniente enxergarmos um heap $H[1\,..n]$ como uma árvore binária (veja definição na Aula 02 ) quase cheia. Isto é,

• $H[1]$ é a raiz da árvore;
• dado $1\leq j\leq \lfloor \frac{n}{2}\rfloor$, os nós $H[2j]$ e $H[2j+1]$ — caso $2j\leq n$ e $2j+1\leq n$ — são os filhos esquerdo e direito de $H[j]$, respectivamente;
• dado $2\leq j\leq n$, o nó $H[j//2]=H\big[\lfloor\frac{j}{2}\rfloor\big]$ é o pai do nó $H[j]$; o nó raiz não tem pai;
• todas as folhas (nós sem filhos) ocorrem em $H\big[\lfloor\frac{j}{2}\rfloor + 1\,..n\big]$;
• todos os nós internos em $H\big[1\,..\lfloor\frac{j}{2}\rfloor - 1\big]$ possuem dois filhos;
• o nó interno $H\big[\lfloor\frac{j}{2}\rfloor]$ tem somente o filho esquerdo se $n$ é par; em caso contrário, ele também tem os dois filhos.

Abaixo, apresentamos uma representação gráfica para o max-heap $H_1=[5,2,5,1,1,4,0,1]$.

Fica claro agora que “a propriedade max-heap” expressa em $(@)$ significa o valor do nó pai é maior ou igual aos dos nós filhos.
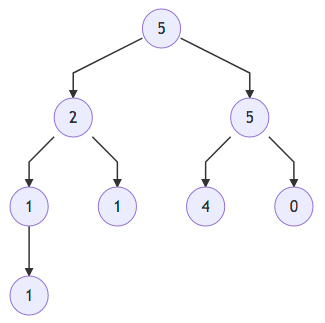
É evidente que a sub-árvore enraizada em cada nó também é um max-heap; no caso, dizemos que ela é um max-sub-heap.

Dizemos que uma lista $H[1\,..n]$ é um quase-max-heap se todas as relações $(@)$ são válidas, com possível exceção das que envolvem a raiz. Isto é, caso a raiz $H[1]$ tenha filhos, podemos ter $H[1] < H[2]$ ou $H[1] < H[3]$, mas as sub-árvores enraizadas em $H[2]$ e $H[3]$ são max-sub-heaps. Claramente, todo max-heap é um quase-max-heap, mas não o contrário.

Problema A4.10: Suponha que $H[1\,..n]$ seja um quase-max-heap. Rearranje os elementos em $H$ de forma que, ao final, $H$ seja um max-heap.

A ideia é “escorregar” o elemento para baixo na árvore até encontrarmos uma posição em que seja maior ou igual a seus filhos. Durante este percurso descendente, os elementos que forem ultrapassados devem subir na árvore. Apresentamos uma versão generalizada da operação sift_down, que lida com quase-max-heaps enraizados em $p$ (e não somente em $1$) e que desconsidera os elementos em $H[m+1\,..n]$ por não fazerem parte do max-heap.

def sift_down (H: [int], m: int, p: int = 1):
  s, x = 2*p, H[p]
  while s <= m:
    if s < m and H[s] < H[s+1]: s += 1
    if x >= H[s]: break
    H[p] = H[s]
    p, s = s, 2*p
  H[p] = x

Nota: a função sift_down faz, no máximo, $2\log n$ comparações entre os elementos de $H$; logo, seu consumo de tempo é $O(\log n)$.

Problema A4.11: Dada uma lista $H[1\,..n]$, rearranje os elementos em $H$ de forma que, ao final, $H$ seja um max-heap.

Utilizando a função sift_down construída acima, nossa tarefa fica fácil e eficiente:

def build_heap (H: [int]):
  n = len (H)
  for i in reversed (range (1, n//2 + 1)):
    sift_down (H, n-1, i)

Uma análise rápida e descuidada atribui tempo $O(n\log n)$ a build_heap. Com uma análise precisa, observa-se que o tempo requerido para a construção de um max-heap por build-heap é $O(n)$.

Problema A4.12: Utilizando o ferramental para max-heaps desenvolvido acima, escreva um algoritmo que recebe uma lista de inteiros $H[1\,..n]$ e rearranja seus elementos de forma que, ao final, eles estejam em ordem crescente.

def heap_sort (H: [int]):
  build_heap (H)
  for m in reversed (range (2, len(H))): 
    H[m], H[1] = H[1], H[m]
    sift_down (H, m-1, 1)

O tempo de heap_sort é $O(n\log n)$.

< escrever nota sobre filas de prioridades >