BCM0505-15 - Processamento da Informação
Aula A08 – 22/05: Matrizes
- Interpolação de pontos no plano por polinômios em uma variável.
Interpolação no Plano: Matriz de Vandermonde
Seja $\mathcal{D}=\{(x_0,y_0),(x_1,y_1),\ldots,(x_n,y_n)\}\subset\mathbb{R}^2$ um conjunto de $n+1$ pontos no plano tais que $x_i\neq x_j$ sempre que $i\neq j$. Dizemos que um polinômio $P:\mathbb{R}\to\mathbb{R}$ interpola os dados $\mathcal{D}$ se $$P(x_j)=y_j \qquad\text{para todo}\qquad j\in\{0,1,\ldots,n\}.$$ Em sendo o caso, $P$ é dito um polinômio interpolador (para $\mathcal{D}$).
Problema A8.1: Dado um conjunto de dados $\mathcal{D}$ com $n+1$ pontos como acima, determine um polinômio interpolador $P$ de grau máximo $n$.
Seja $P$ um polinômio de grau $n$ na variável $x$ de forma
$$
P(x) = p_n x^n + p_{n-1}x^{n-1} + \cdots + p_2 x^2 + p_1 x + p_0.
$$
Precisamos determinar valores para os coeficientes $p_n, p_{n-1}, \ldots, p_0$ de forma que $P(x_j)=y_j$, para todo
$j\in\{0,1,\ldots,n\}$. Realizando estas $n+1$ substituições, obtemos um sistema linear em $p_n, p_{n-1}, \ldots, p_0$:
$$
\left(\begin{array}{cccccc}
x_0^n & x_0^{n-1} & x_0^{n-2} & \cdots & x_0 & 1 \\
x_1^n & x_1^{n-1} & x_1^{n-2} & \cdots & x_1 & 1 \\
\vdots& \vdots & \vdots & &\vdots & \vdots \\
x_n^n & x_n^{n-1} & x_n^{n-2} & \cdots & x_n & 1
\end{array}\right)
\left(\begin{array}{c}
p_n \\ p_{n-1} \\ \vdots \\ p_0
\end{array}\right) =
\left(\begin{array}{c}
y_0 \\ y_1 \\ \vdots \\ y_n
\end{array}\right).
$$
O algoritmo de eliminação gaussiana (visto na aula
A07
) naturalmente se apresenta como uma alternativa para
a resolução do sistema acima. A matriz à esquerda é conhecida como Matriz de Vandermonde e possui, em geral, um número de
condicionamento alto (não vamos entrar em detalhes aqui). Isso implica em frequente acúmulo de erros numéricos durante o
processo de escalonamento. Logo, os coeficientes determinados via eliminação gaussiana no sistema acima tendem a não funcionar.
Felizmente, uma mudança de base (de monômios para polinômios de Lagrange) resolve a questão.
Exercício 1: Resolva o sistema acima via eliminação gaussiana e teste (numericamente) a qualidade do polinômio interpolador obtido.
Exercício 2: Mostre que existe um único polinômio de grau menor ou igual a $n$ que interpola os $n+1$ pontos em $\mathcal{D}$. Dica: use o teorema fundamental da álgebra.
Interpolação no Plano: Polinômios de Lagrange
Para cada $j\in\{0,1,\ldots,n\}$, defina $$ L_{n,j}(x) := \prod_{k\neq j} \frac{x-x_k}{x_j-x_k}, $$ em que $L_{n,j}$ é um polinômio de grau $n$ em $x$. Não é difícil perceber, para cada $x_k$, que $$ L_{n,j}(x_k) = \begin{cases} 1 & \text{se}~ j=k,\\ 0 & \text{em caso contrário.} \end{cases} $$ Temos, então, que a combinação linear $$ P(x) = \sum_{j=0}^{n} y_j L_{n,j}(x) $$ é um polinômio interpolador para $\mathcal{D}$ de grau $n$. Mais do que isso, $P(x)$ é o único polinômio de grau $n$ que interpola $\mathcal{D}$.
Os polinômios $L_{n,j}(x)$ são conhecidos coletivamente como a base de polinômios de Lagrange. $P(x)$ é o polinômio interpolador obtido pelo método de interpolação de Lagrange.
Um código que avalia $P$ em um ponto $z\in\mathbb{R}$ é obtido diretamente da descrição acima. Vamos fazer algo mais interessante.
Vamos definir uma função lagrange_polynomial que:
- recebe duas listas não vazias $x[0\,..n]$ e $y[0\,..n]$, que armazenam as abcissas e ordenadas dos pontos em $\mathcal{D}$, respectivamente,
- devolve uma função de um parâmetro que quando instanciada para um valor $z$, devolve $P(z)$.
from math import prod
def lagrange_polynomial (x: [float], y: [float]):
def L (j: int):
return lambda z: prod ((z - x[k])/(x[j] - x[k]) for k in range (len (x)) if k != j)
return lambda z: sum (y[j]*L(j)(z) for j in range (len (x)))
O exemplo que segue
x = [-9, -4, -1, 7]
y = [ 5, 2, -2, 9]
P = lagrange_polynomial (x, y)
x_range = list (range (x[0]-1, x[-1]+2))
for xj, yj in zip (x_range, list (map (P, x_range))):
print ("{: 7.3f},{: 7.3f}".format (xj, yj))
produz o resultado (para mais informações sobre formatação de strings, veja a
documentação
)
-10.000, 3.910
-9.000, 5.000
-8.000, 5.358
-7.000, 5.110
-6.000, 4.384
-5.000, 3.305
-4.000, 2.000
-3.000, 0.597
-2.000, -0.779
-1.000, -2.000
0.000, -2.940
1.000, -3.472
2.000, -3.469
3.000, -2.805
4.000, -1.352
5.000, 1.015
6.000, 4.423
7.000, 9.000
8.000, 14.872
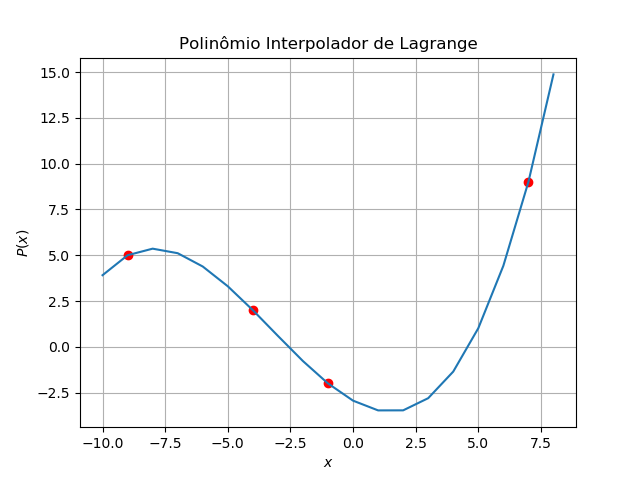
que pode melhor ser visualizado em um gráfico (os pontos em vermelho correspondem aos dados; o polinômio interpolados aparece em azul).
from matplotlib import pyplot as plt
plt.plot (x, y, 'ro')
plt.plot (x_range, list (map (P, x_range)))
plt.xlabel (r'$x$')
plt.ylabel (r'$P(x)$')
plt.title ('Polinômio Interpolador de Lagrange')
plt.grid (True)
plt.show()
Aproveitando a oportunidade, podemos gravar a lista de valores $(x_j,y_j)$ impressa acima em um arquivo texto chamado lagrange_example.csv — a extensão “csv” significa comma-separated values, ou valores separados por vírgulas — e utilizar o código abaixo para lê-los de tal arquivo.
def read_data (fname: str):
x, y = [], []
with open (fname, 'r') as f:
for line in f:
(_x, _y) = line.split (',')
x.append (float (_x))
y.append (float (_y))
return (x, y)
data_fname = 'lagrange_example.csv'
(x, y) = read_data (data_fname)
Mais detalhes sobre leitura e gravação de aquivos em Python podem ser obtidos na documentação.
Para efeitos de cálculo e de aproximação, o método acima (em que o polinômio é representado implicitamente como uma função) é usual e desejado. Se desejarmos obter explicitamente os coeficientes $p_n, p_{n-1}, \ldots, p_0$, no entanto, para representar $P$ como feito na aula A05, um pouco mais de trabalho é necessário.
Fazendo $N=\{0,1,\ldots,n\}$, não é difícil perceber que $$ \prod_{k=0}^{n} (x-x_k) = \sum_{k=0}^{n} (-1)^{k} \left(\sum_{S\in\binom{N}{k}} \prod_{i\in S} x_i\right)x^{n-k}. $$ Pense na fórmula acima como uma generalização do teorema do binômio de Newton. De fato, existem $n+1$ produtos de cláusulas da forma $(x-x_k)$ no lado esquerdo, em que $x$ é uma variável e todos os $x_k$ são valores. A expansão do lado esquerdo consiste na soma de todas as $2^n$ seleções possíveis dentre os dois literais ($x$ e $x_k$) de cada cláusula. Fatorando-se os termos que têm a mesma potência de $x$, obtém-se a expressão do lado direito.
def lagrange_coef (x: [float], y: [float]) -> [float]:
P = [0] * (m := len (x)) # m == n+1
z = [prod (x[j] - x[k] for k in range (m) if k != j) for j in range (m)]
.
.
.
Antes de deixarmos esta seção, observe que a alteração, inclusão ou remoção de um ponto em $\mathcal{D}$ requer que o polinômio interpolador de Lagrange seja completamente recalculado. Para contornar esse fato indesejável, outras bases de polinômios foram propostas como a de Newton, de Neville, de Fourier, de Chebyshev, entre outras.
Interpolação no Plano: Polinômios de Neville
Seja $p_{i,j}$ um polinômio de grau $j-i$ que interpola os pontos $(x_k,y_k)$ para $k=i,i+1,\ldots,j$. Temos que $p_{i,j}$ satisfaz a seguinte relação de recorrência: $$ \begin{align*} p_{i,i}(x) &= y_i, && 0\leq i\leq n,\\ p_{i,j}(x) &= \frac{(x-x_j)p_{i,j-1}(x) - (x-x_i)p_{i+1,j}(x)}{x_i - x_j}, && 0\leq i< j\leq n. \end{align*} $$
Calculando a recorrência para $P(x)=p_{0,n}(x)$, temos o polinômio interpolador de Neville para $\mathcal{D}$.
Abaixo, um exemplo mostrando a estrutura do cálculo de $p_{0,4}$.
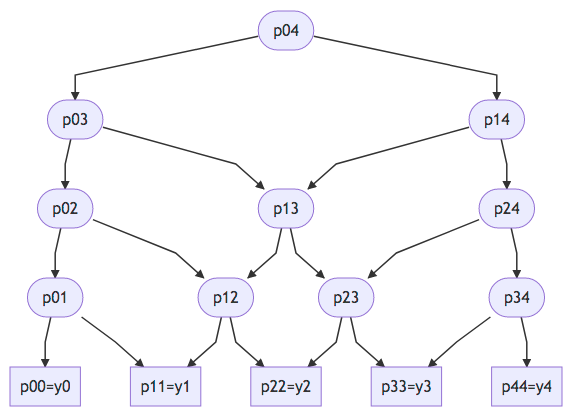
Não é difícil perceber que polinômios de menor grau são repetidamente utilizados — tanto mais quanto menor o grau. Em outras palavras, a recorrência de Neville apresenta superposição de subproblemas. Podemos evitar recálculos avaliando a recorrência em ordem reversa (bottom-up) e armazenando resultados calculados em uma matriz, como segue. $$ \left(\begin{array}{ccccccc} p_{0,0} & p_{0,1} & p_{0,2} & p_{0,3} & p_{0,4} & \cdots & \boldsymbol{p_{0,n}} \\ & p_{1,1} & p_{1,2} & p_{1,3} & p_{1,4} & \cdots & p_{1,n} \\ & & p_{2,2} & p_{2,3} & p_{2,4} & \cdots & p_{2,n} \\ & & & p_{3,3} & p_{3,4} & \cdots & p_{3,n} \\ & & & & p_{4,4} & \cdots & p_{4,n} \\ & & & & & \ddots & \vdots \\ & & & & & & p_{n,n} \\ \end{array}\right) $$ Ou seja, preenchemos tal matriz começando na diagonal principal e procedemos, diagonal por diagonal, em direção ao canto superior direito que contém o resultado desejado $\boldsymbol{p_{0,n}}$.
def neville_polynomial_mtx (x: [float], y: [float], z: float) -> float:
m = len (x) # m == n+1
p = [[(y[i] if i == j else 0) for j in range (m)] for i in range (m)]
for k in range (1, m):
for i in range (m - k):
j = k + i
p[i][j] = ((z - x[j]) * p[i][j-1] - (z - x[i]) * p[i+1][j]) / (x[i] - x[j])
return p[0][m-1]
Ponderando um pouco mais, observamos que cada diagonal é utilizada somente pela diagonal imediatamente acima. Logo, podemos utilizar um vetor.
def neville_polynomial (x: [float], y: [float]):
def N (z: float) -> float:
p = [yj for yj in y]
for k in range (1, len (x)):
for i in range (len (x) - k):
p[i] = ((z - x[k+i]) * p[i] - (z - x[i]) * p[i+1]) / (x[i] - x[k+i])
return p[0]
return lambda z: N (z)
O exemplo
x = [-9, -4, -1, 7]
y = [ 5, 2, -2, 9]
Q = neville_polynomial (x, y)
x_range = list (range (x[0]-1, x[-1]+2))
for xj, yj in zip (x_range, list (map (Q, x_range))):
print ("{: 7.3f},{: 7.3f}".format (xj, yj))
produz o mesmo resultado — afinal, o polinômio interpolador de grau menor ou igual a $n$ é único.