BCM0505-15 - Processamento da Informação

Aula A09 – 29/05: Grafos em Matrizes

• Matriz de adjacências.
• Busca em largura e caminhos mínimos.
• Algoritmos de Dijkstra e Floyd-Warshall.

Grafos e Matrizes de Adjacências

Grafos e digrafos são formalismos matemáticos adequados para descrever e manipular relações binárias entre objetos.
Formalmente, um grafo é um par ordenado $(V,E)$, em que:

• $V$ é um conjunto finito cujos elementos são chamados vértices, e
• $E\subseteq\binom{V}{2}$ é um conjunto de arestas, cada qual um par não ordenado de vértices.

Nota: $\binom{V}{2} := \{S\subseteq V:|S|=2\}$ é o conjunto de todos os subconjuntos com $2$ elementos de $V$; se $|V|=n$, claramente $\big|\binom{V}{2}\big| = \binom{|V|}{2} = \binom{n}{2}.$

Uma miríade de situações podem ser modeladas através de grafos. Para nossa aplicação, vamos considerar que os vértices representam pontos geográficos de interesse (como locais, esquinas, cidades, países, pontos turísticos, ou outros) e as arestas indicam a existência de ligações entre pares de pontos como ruas, estradas, rotas, etc. Grafos modelam relações binárias simétricas e, portanto, pensamos em ruas, estradas, rotas como entes de “mão dupla.”

No que segue, vamos sempre supor que um grafo $G=(V,E)$ possui $n\geq 0$ vértices e $m\geq 0$ arestas, com $V=\{0,1,2,\ldots,n-1\}$. O grafo $G$ pode então ser representado através de uma matriz $A(G)\in\{0,1\}^{n\times n}$, denominada matriz de adjacências de $G$, definida como: $$ A(G)[i][j] = \begin{cases} 1 & \text{se}~\{i,j\}\in E,\\ 0 & \text{em caso contrário}, \end{cases} $$ para $i,j\in V$. Em outras palavras, se os vértices $i$ e $j$ são adjacentes (existe uma aresta entre eles), as entradas $A(G)[i][j]$ e $A(G)[j][i]$ são iguais a $1$; $A(G)[i][j] = A(G)[j][i] = 0$ em caso contrário. Note que podemos utilizar True no lugar de $1$ e False em vez de $0$, deixando a representação mais econômica.

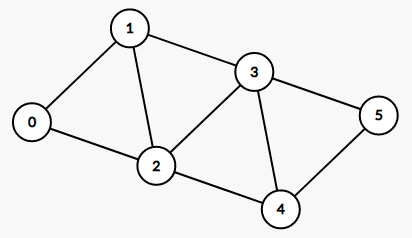
Considere o exemplo abaixo, em que temos um grafo $G_1=(V,E)$ com $V=\{0,1,2,3,4,5\}$ e $$E=\big\{\{0,1\},\{0,2\},\{1,2\},\{1,3\},\{2,3\},\{2,4\},\{3,4\},\{3,5\},\{4,5\}\big\}.$$ Podemos visualizar $G_1$ como

e representá-lo como $$ A(G_1) = \left(\begin{array}{cccccc} 0 & 1 & 1 & 0 & 0 & 0 \\ 1 & 0 & 1 & 1 & 0 & 0 \\ 1 & 1 & 0 & 1 & 1 & 0 \\ 0 & 1 & 1 & 0 & 1 & 1 \\ 0 & 0 & 1 & 1 & 0 & 1 \\ 0 & 0 & 0 & 1 & 1 & 0 \end{array}\right). $$ Claramente, $A(G_1)$ é simétrica.

Exercício 1: Um triângulo em um grafo $G=(V,E)$ é formado por três vértices distintos $u,v,w\in V$ tais que as arestas $\{u,v\}$, $\{u,w\}$ e $\{v,w\}$ pertencem a $E$. Escreva uma função que recebe a matriz de adjacências de um grafo $G$ e determina o número de triângulos em $G$.

Para um grafo $G=(V,E)$, sejam $s$ e $t$ dois vértices em $V$. Um $(s,t)$-caminho em $G$ é uma sequência de vértices $$P=\langle s=v_0,v_1,\ldots,v_k=t\rangle$$ tal que $v_i\neq v_j$ quando $i\neq j$ e $\{v_{i-1},v_i\}\in E$, para $0\leq i\leq k$. Em outras palavras, em um $(s,t)$-caminho todos os vértices são distintos e vai-se de um vértice a outro, começando em $s$ e chegando a $t$ (ou vice-versa) percorrendo-se a aresta que os conecta (não há saltos).

O comprimento de um $(s,t)$-caminho $P$, denotado por $\ell(P)$ é igual ao número de arestas que são percorridas de uma extremidade a outra. No exemplo acima, temos $\ell(P) = k$. Naturalmente, dados quaisquer $s,t\in V$, pode não haver um $(s,t)$-caminho em $G$ e, caso exista, ele não precisa ser único — tudo depende da estrutura do grafo, expressa pelas arestas.

Voltando ao exemplo $G_1$, se escolhermos $s=0$ e $t=5$ temos que alguns $(0,5)$-caminhos são, $$\langle 0, 1, 3, 5\rangle,~\langle 0, 2, 3, 5\rangle,~\langle 0, 1, 2, 3, 5\rangle,~\langle 0, 1, 2, 3, 4, 5\rangle,$$ de comprimento $3$, $3$, $4$ e $5$, respectivamente. Claramente existem outros; quantos? Observe ainda que $G_1$ tem uma característica especial: para quaisquer $s,t\in V$, é possível determinar um $(s,t)$-caminho. 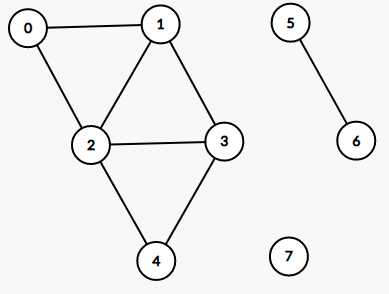Dizemos que $G_1$ — e qualquer grafo com esta propriedade — é conexo. Nem todos os grafos são conexos: no exemplo $G_2$ abaixo não existe um $(2,7)$-caminho.

$G_2$ é um grafo com $3$ componentes conexos — não vamos definir formalmente tal conceito, mas ele é óbvio à partir da figura.

Caminhos Mínimos

Sejam um grafo $G=(V,E)$ e $c:E\to\mathbb{R}_{\geq 0}$ uma função que associa a cada aresta $e\in E$ um custo real não negativo $c(e)$. No caso mais simples, chamado unitário, $c=1$ é a função constante que associa o valor $1$ a cada aresta $e$ de $G$.

Sejam $s,t\in V$ e seja $P=\langle s=v_0,v_1,\ldots,v_k=t\rangle$ um $(s,t)$-caminho em $G$. O custo de $P$ é dado por $$c(P) := \sum_{i=1}^k c(\{v_{i-1},v_i\}),$$ isto é, o custo de $P$ é a soma do custo das arestas que o compõem. Claramente, no caso unitário, temos que $c(P)=\ell(P)$; nos demais casos, a diferença entre $c(P)$ e $\ell(P)$ pode ser arbitrária.

Como aplicação, imagine que o custo de uma aresta representa:

• o tempo necessário para percorrê-la à velocidade máxima permitida, ou
• ao comprimento, em quilômetros, do trecho de pavimento que descreve, ou
• o montante, em litros, de combustível requerido para ir de um vértice ao outro, ou
• a quantia a ser dispendida em pedágios durante aquele pedaço da viagem, ou
• a variação de temperatura de um ponto a outro, ou
• virtualmente, qualquer coisa que seja quantificável.

Seja $\mathcal{P}(s,t)$ o conjunto de todos os $(s,t)$-caminhos em $G$ e defina $$c^*(s,t) := \min\big\{c(P):P\in\mathcal{P}(s,t)\big\}$$ como o custo mínimo dentre todos os $(s,t)$-caminhos em $G$. Qualquer caminho $P^*\in\mathcal{P}(s,t)$ tal que $c(P^*)=c^*(s,t)$ é dito um $(s,t)$-caminho de custo mínimo (ou simplesmente um $(s,t)$-caminho mínimo quando o custo for subentendido; quando o custo for unitário, é comum dizer-se um $(s,t)$-caminho de comprimento mínimo). Naturalmente, se não existir um $(s,t)$-caminho em $G$, tem-se que $\mathcal{P}(s,t)=\emptyset$ e que $c^*(s,t)=\infty$.

Busca em Largura (BFS)

No que segue, sempre que for dado um grafo $G$, entenda como sua matriz de adjacências $A(G)$.

Problema A9.1: Dados um grafo $G=(V,E)$, uma função de custo $c$ unitária e dois vértices $s,t\in V$, determine $c^*(s,t)$, o custo de um caminho mínimo entre $s$ e $t$.

Suponha que $P^*=\langle s=v_0,v_1,\ldots,v_k=t\rangle$ é um caminho mínimo entre $s$ e $t$. Não é difícil perceber que $P^*$ tem sub-estrutura ótima, isto é, para qualquer vértice $v_j$ com $1\leq j<k$, temos que $P^*$ é a concatenação dos caminhos $$ S = \langle s=v_0,v_1,\ldots,v_j\rangle \qquad\text{se}\qquad T = \langle v_j,\ldots,v_k=t\rangle, $$ em que $S$ é um caminho mínimo entre $s$ e $v_j$ e o mesmo vale para $T$ entre $v_j$ e $t$.

De fato, temos que $c(P^*)=c(S)+c(T)$. Se $S$ não é mínimo, existe um caminho $R=\langle s=u_0,u_1,\ldots,u_\ell=v_j\rangle$ tal que $c(R)<c(S)$, o que implica que $R$ concatenado com $T$ é um caminho entre $s$ e $t$ de custo $c(R)+c(T)<c(P^*)$. Isso contraria a hipótese de que $P^*$ é ótimo.

O argumento acima aliado ao fato de que os custos das arestas são unitários fornece uma ideia algorítmica conhecida como busca em largura (em inglês, breadth-first search ou BFS).

O algoritmo mantém limitantes superiores aos custos dos caminhos mínimos, melhorando-os (i.é, baixando os limitantes superiores) até que os valores corretos tenham sido determinados. Inicialmente, somente o vértice de origem $s$ tem o custo correto, que é $0$. Todos os demais tem um custo $\infty$ — afinal, nem sabemos se é possível atingi-los à partir de $s$. O algoritmo procede então em “ondas:” todos os vértices à distância $1$ de $s$ têm seus custos determinados; após, todos os vértices à distância $2$ de $s$ têm seus custos determinados; assim sucessivamente até que todos os vértices atingíveis à partir de $s$ tenham custos conhecidos. De suma importância: como os custos são unitários, não há possibilidade de um custo ter sido determinado erroneamente, com folga.

Como a função de custo $c$ é unitária, ela não precisa ser passada como parâmetro.

from math import inf as oo

# Recebe uma matriz de adjacências A de um grafo G e um vértice origem s de G.
# Devolve um vetor d tal que d[j] é o comprimento de um caminho mínimo entre s e j.
def BFS (A: [[bool]], s: int) -> [int]:
  d = [oo] * (n := len (A)); d[s] = 0
  Q = [s]
  while Q != []:
    i = Q.pop (0)
    for j in range (n):
      if A[i][j] and d[i] + 1 < d[j]:
        d[j] = d[i] + 1
        Q.append (j)
  return d

Não é difícil perceber que cada vértice de $G$ entra no máximo uma vez na fila $Q$ e que cada aresta é visitada $0$ ou $2$ vezes. Logo, o tempo requerido por BFS é linear no tamanho da descrição de $G$: $O(n+m)$.

Problema A9.2: Estenda o Problema A9.1 e determine, conjuntamente, um $(s,t)$-caminho mínimo em $G$ — se possível, claro.

Observe que quando a distância de um nó $j$ é baixada de infinito a um valor inteiro na linha d[j] = d[i] + 1, temos também a informação de que passamos por $i$ para chagar a $j$ em um $(s,j)$-caminho mínimo. Precisamos somente guardar essa informação. Fazemos isso através de um outro vetor $p[0\,..n-1]$, o vetor de predecessores:

• no início cada nó aponta para sí mesmo, isto é, $p[j]=j$; isso indica a não existência de um predecessor para $j$;
• ao ser visitado pela primeira e única vez na busca em largura, $p[j]$ passa a apontar para $i$;
• ao final, $$p[j] = \begin{cases} j & \text{se}~ j=s ~\text{ou}~ d[j]=\infty,\\ i & \text{se}~ d[j]=d[i]+1. \end{cases}$$

from math import inf as oo

# Recebe uma matriz de adjacências A de um grafo G e um vértice origem s de G.
# Devolve um vetor d tal que d[j] é o comprimento de um caminho mínimo entre s e j,
#         um vetor p tal que p[j] é o predecessor de j em um caminho mínimo de s a j.
def USSSP (A: [[bool]], s: int) -> [int]:
  d = [oo] * (n := len (A)); d[s] = 0
  p = [j for j in range (n)]
  Q = [s]
  while Q != []:
    i = Q.pop (0)
    for j in range (n):
      if A[i][j] and d[i] + 1 < d[j]:
        d[j] = d[i] + 1
        p[j] = i
        Q.append (j)
  return d, p

Nota: USSSP = Unitary Single Source Shortest Path.

Se o grafo é conexo, pode-se reconstruir um $(s,t)$-caminho mínimo agora com o código que segue.

def print_path (p: [int], t: int):
  if p[t] == t: 
    print (t, end = " ")
  else
    print_path (p, p[t])
    print ("-->", t, end = " ")

Exercício 2: Escreva uma versão apropriada para o caso de grafos não necessariamente conexos.

Problema A9.3: Dados um grafo $G=(V,E)$, determine se $G$ é conexo.

from math import inf as oo
def is_connected (A: [[bool]]) -> bool:
  d = BFS (A, 0)
  return all (di < oo for di in d)

Exercício 3: Dado um grafo $G=(V,E)$, determine o número de componentes conexos de $G$.

Custos Não Negativos e Algoritmo de Dijkstra

Problema A9.4: Dados um grafo $G=(V,E)$ conexo, uma função de custo $c:E\to\mathbb{R}_{\geq 0}$ e um vértice $s\in V$, determine $(s,t)$-caminhos mínimos em $G$ para todo vértice $t\in V$.

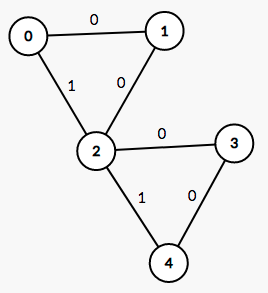
Quando a função de custo não é unitária — mas ainda é não negativa — a simples ordem de descobrimento imposta pela fila na busca em largura não mais garante correção. De fato, o grafo abaixo mostra que um $(0,4)$-caminho de custo mínimo é $P_1=\langle 0,1,2,3,4\rangle$, de custo $C(P_1)=0$, enquanto um $(0,4)$-caminho de comprimento mínimo, devolvido pela busca em largura, é $P_2=\langle 0,2,4\rangle$, de custo $c(P_2)=2$. Nota: os números próximos às arestas são os custos das mesmas.

Certamente, a sub-estrutura ótima continua presente nos casos de custos não uniforme. A diferença, então, reside na ordem de descoberta dos vértices e no fato de que agora, é possível revisitar um vértice mais tarde a um custo menor. Utilizando-se judiciosamente uma fila de prioridades (veja heaps na aula A04 ) no lugar de uma fila simples resolve o problema.

Uma fila de prioridades, neste caso, é uma estrutura $\mathcal{F}$ que armazena vértices, cada qual com um valor numérico associado que descreve a prioridade do vértice. Vamos supor que valores pequenos indicam alta prioridade e que valores grandes indicam baixa prioridade. Inicialmente, $\mathcal{F}$ é vazia. Os vértices são inseridos em $\mathcal{F}$ juntamente com suas prioridades. A qualquer momento, a prioridade de um dado vértice pode aumentar ou diminuir. No momento de remoção, o vértice de maior prioridade deixa $\mathcal{F}$.

Vamos fazer uma das implementações mais simples: utilizar um vetor $Q[0\,..n-1]$ em que $Q[i]$ armazena a prioridade do vértice $i$. Para que tudo funcione, vamos identificar alta prioridade com baixa distância e, assim, armazenar o custo atual de $s$ a $i$ em $Q[i]$. Vértices $j$ que estejam “fora” da fila terão valores $Q[j]=\infty$.

Precisamos de uma estrutura para armazenar os custos $c(\cdot)$ das arestas. Sem pensar muito, podemos estender a matriz de adjacências $A(G)$ para a forma: $$ A(G)[i][j] = \begin{cases} c(\{i,j\}) & \text{se}~\{i,j\}\in E,\\ -1 & \text{em caso contrário}, \end{cases} $$ para $i,j\in V$. Claro que o valor $-1$ funciona para indicar a ausência de uma aresta porque os custos são não negativos. Assim como na versão original, esta representação usa o dobro do espaço necessário. Não vamos nos preocupar com isso, no entanto.

from math import inf as oo

# Recebe uma matriz de adjacências estendida A de um grafo G e um vértice origem s de G.
# Devolve um vetor d tal que d[j] é o comprimento de um caminho mínimo entre s e j,
#         um vetor p tal que p[j] é o predecessor de j em um caminho mínimo de s a j.
def dijkstra (A: [[bool]], s: int) -> [int]:
  d = [oo] * (n := len (A)); d[s] = 0
  p = [j for j in range (n)]
  Q = [s]

  while len (Q) != 0:
    i = min (range (len (Q)), key = lambda j: d[Q[j]])
    Q.pop (i)  
    

  < terminar o código >

  while True:
    i = min (range (n), key = lambda j: Q[j])
    if i = oo: break

    i = Q.pop (0)
    for j in range (n):
      if A[i][j] and d[i] + 1 < d[j]:
        d[j] = d[i] + 1
        p[j] = i
        Q.append (j)


  return d, p

Como codificado, o algoritmo de Dijkstra consome tempo $O(mn)$.

Digrafos

Intuitivamente, digrafos são as contrapartes não simétricas a grafos, possibilitando assim direções e orientações de um vértice a outro.
Formalmente, um digrafo é um par ordenado $(V,R)$, em que:

• $V$ é um conjunto finito cujos elementos são chamados vértices, e
• $R\subseteq V\times V$ é um conjunto de arcos, cada qual um par ordenado de vértices.

Para um arco $r=(i,j)\in R$, dizemos que o vértice $i$ é a cauda de $r$ e que $j$ é sua cabeça. Assim, entendemos o arco $r$ como orientado de $i$ para $j$. O arco reverso a $r$ é $r'=(j,i)$. Note que $r\neq r'$. Dizemos que $r$ e $r'$ são anti-paralelos. Um laço é um arco da forma $(i,i)$.

Nota: em poucas palavras, uma aresta é um subconjunto com $2$ elementos e um arco é uma tupla com $2$ elementos; tuplas possuem ordem, subconjuntos não; logo, arestas são simétricas e arcos possuem direção específica.

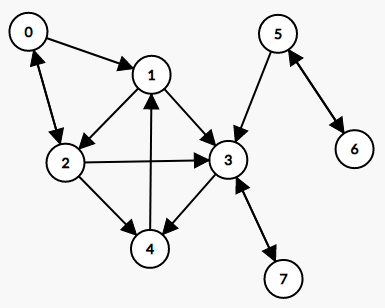
Abaixo, um exemplo de um digrafo $D_1=(V,R)$ com $V=\{0,1,2,3,4,5,6,7\}$, e $$R = \big\{(0,1),(0,2),(1,2),(1,3),(2,0),(2,3),(2,4),(3,4),(3,7),(4,1),(5,3),(5,6),(6,5),(7,3)\big\}.$$

Definimos a matriz de adjacências de um digrafo $D=(V,R)$ de forma semelhante à de um grafo: $A(D)\in\{0,1\}^{n\times n}$ é dada por: $$ A(D)[i][j] = \begin{cases} 1 & \text{se}~(i,j)\in R,\\ 0 & \text{em caso contrário}, \end{cases} $$ para $i,j\in V$. Valores Booleanos podem ser utilizados em vez de $0$ e $1$ e ela pode ser estendida para custos não negativos de forma similar ao que fizemos para grafos. Claramente, $A(D)$ é simétrica se e somente se para todo arco $r\in R$, seu anti-paralelo também pertence a $R$.

Abaixo, a matriz de adjacências do digrafo $D_1$: $$ A(D_1) = \left(\begin{array}{cccccccc} 0 & 1 & 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 1 & 0 & 0 & 0 & 0 \\ 1 & 0 & 0 & 1 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & 1 \\ 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 \end{array}\right). $$

A matriz de custos pode ser adaptada para digrafos de forma semelhante.

Utilize um tempo agora para se convencer de que os algoritmos de busca em largura e Dijsktra que desenvolvemos acima funcionam corretamente se uma matriz de adjacências fornecida for a de um digrafo (em vez da de um grafo).

Algoritmo de Floyd-Warshall

Dado um digrafo $D=(V,R)$, é possível utilizarmos o algoritmo de Dijkstra $n-1$ vezes (em que $n=|V|$) e determinarmos todos os $(s,t)$-caminhos mínimos em $D$, para todos os pares de vértices $s$ e $t$. Uma forma mais fácil e rápida consiste na utilização do algoritmo desenvolvido por Floyd e por Warshall.

Vamos fixar a ordenação numérica natural dos vértices em $V=\{0,1,\ldots,n-1\}$. Para todo par $i,j\in V$ e todo $k=-1,0,1,2,\ldots,n-1$, defina $\mathsf{dist}_k(v_i,v_j)$ como o custo do melhor caminho de $i$ a $j$ podendo utilizar somente $0,1,\ldots,k$ como vértices internos (se $k=-1$, nenhum vértice pode ser utilizado). Temos então a seguinte recorrência: $$ \mathsf{dist}_k(i,j) = \begin{cases} 0 & \text{se}~ i=j,\\ c\big((i,j)\big) & \text{se}~ i\neq j~ \text{e}~ k=-1\\ \min \big\{\mathsf{dist}_{k-1}(i,j), \mathsf{dist}_{k-1}(i,k) + \mathsf{dist}_{k-1}(k,j)\big\} & \text{se}~ i\neq j~ \text{e}~ 0\leq k\leq n-1. \end{cases} $$ Não é difícil perceber que ela fornece um algoritmo para o cômputo dos caminhos de peso mínimo entre todos os pares de vértices de $D$, e que o tempo requerido por este algoritmo é $\Theta(n^3)$. A implementação fica mais clara em forma matricial.

Seja $W\in\mathbb{R}_\geq^{V\times V}$ a matriz de pesos do digrafo $D$, isto é, para todo $i,j\in V$, $$ W_{i,j} = \begin{cases} 0 & \text{se}~ i=j,\\ c\big((i,j)\big) & \text{se}~ i\neq j~ \text{e o arco}~ (i,j)\in R,\\ \infty & \text{em caso contrário}. \end{cases} $$ Temos então, a codificação abaixo.

def floyd-warshall (D: [[bool]], W: [[float]]):
  n = len (D)
  for k in range (n):
    for i in range (n):
      for j in range (n):
        W[i][j] = min (W[i][j], W[i][k] + W[k][j])

Para a matriz $W$ devolvida, temos que $W_{i,j} = \mathsf{dist}_{n-1}(i,j)$.

Listas de Adjacências

Você deve ter observado que se os números de arestas ou arcos forem lineares (ou de ordem ainda menor) nos números de vértices, isto é, se os grafos ou digrafos forem esparsos, um número grande de entradas nulas é armazenado nas respectivas matrizes de adjacências. Semelhante ao caso dos polinômios esparsos da aula A05, isso é indesejável. Uma estrutura de dados que enfrenta esse problema é chamada listas de adjacências. Apesar de ser uma estrutura bem simples, não será coberta nesse curso (por questões de limitação). Para grafos ou digrafos densos, matrizes de adjacências são as mais adequadas.