BCM0505-15 - Processamento da Informação

Aula 02 – 14/02

Busca em Sequências Ordenadas

Considere o seguinte problema:

Problema 2.1: Dados uma sequência $$A = [ a_0,a_1,\ldots,a_{n-1} ]$$ de $n\geq 0$ elementos em ordem crescente, isto é, tal que $$a_0 \leq a_1 \leq\ldots\leq a_{n-1},$$ e um elemento $x$, devolva um índice $-1\leq j\leq n$ tal que $a_{j-1} < x\leq a_j$.

A menos do valor a ser devolvido quando $x$ não ocorre em $A$, o algoritmo de busca sequencial que desenvolvemos na aula passada resolve o problema acima — afinal, ele funciona para qualquer sequência $A$, inclusive as ordenadas. Dois pontos, no entanto, nos motivam a desenvolver uma nova versão:

• Quando $x\not\in A$, aquele algoritmo devolve $n$, o número de elementos em $A$. Observe que tal valor possui a seguinte semântica: $x$ não ocorre em $A$ e pode ser adicionado na posição $n$. No caso de uma sequência ordenada, este raciocínio é quebrado: inserir $x$ na posição $n$ pode violar a ordenação de $A$ após a inserção. Por isso, decidimos devolver o índice $j$ especificado: se $x$ ocorre em $A$, a primeira posição em que ele ocorre é $j$; em caso contrário, ele não ocorre e deveria ser adicionado na posição $j$ para manter a ordenação.
• Quando estamos procurando por $x$ em $A$ e encontramos um valor $y>x$, temos certeza de que $x\not\in A$. Não há necessidade de continuarmos varrendo $A$ até o final.

Busca Sequencial Ordenada

O código abaixo implementa essas duas modificações.

# Busca Sequencial Ordenada
# - recebe_: uma lista A de inteiros em ordem crescente e um elemento x
# - devolve: um índice j tal que A[j-1] < x <= A[j]
#
def sorted_seq_search (A, x):
  j, n = 0, len(A)
  while j < n and A[j] < x:
    j = j + 1
  return j

Note que, obviamente, ele é muito parecido com o da aula passada. O pior caso agora ocorre quando $x$ é maior que qualquer valor em $A$, implicando em um consumo de tempo linear (no pior caso) no comprimento da sequência.

Busca Binária

Explorando melhor a hipótese de ordem entre os elementos de $A$, podemos fazer algo superior.

Suponha, por um momento, que estamos procurando $x$ na sub-sequência $A[e\,..d]=[a_{e+1},a_{e+2},\ldots,a_{d-2},a_{d-1}]$, com $-1\leq e< d\leq n$. Se $e=d-1$, temos um único elemento e o índice desejado é $d$. Em caso contrário, seja $m=\lfloor(e+d)/2\rfloor$. Comparando $a_m$ com $x$, podemos ter

• $a_m < x$, o que implica certamente que $x\not\in A[e\,..m]$ — lembre-se que $A$ está em ordem crescente; logo, podemos descartar todo o lado esquerdo e concentrar a busca no lado direito; isto é feito atualizando $e=m$.
• $a_m\geq x$, o que implica que a primeira ocorrência de $x$ em $A$ está no lado esquerdo; podemos, assim, desconsiderar o lado direito, fazendo $d=m$.

Independente do caso, descartamos aproximadamente metade dos elementos que estavam em $A[e\,..d]$ no início da iteração.

Inicializando $e=-1$ e $d=n$, temos o cenário envolvendo toda a sequência $A$. Repetindo o processo descrito, mais cedo ou mais tarde atingimos o caso em que a sub-sequência possui um único elemento. Não é difícil perceber que se $x$ ocorre em $A$, sua primeira ocorrência é no índice devolvido; se $x\not\in A$, o índice devolvido também é o desejado.

Resta checarmos um caso: e quando $A$ for vazia? Observe que se $A=[\,]$, teremos inicialmente que $e=-1$ e $d=0$. O algoritmo termina e devolve $0$, que é o valor esperado.

A título de curiosidade, os invariantes são:

• $-1\leq e\leq m< d\leq n$,
• ou $e$ aumenta, ou $d$ diminui a cada passo,
• $x\not\in A[0\,..e]\cup A[d\,..n-1]$.

Ao final, $x$ ocorre ou deveria ocorrer no índice $d$.

O código abaixo implementa esta ideia.

# Busca Binária
# - recebe_: uma lista A de inteiros em ordem crescente e um elemento x
# - devolve: um índice d tal que A[d-1] < x <= A[d]
#
def bin_search (A, x):
  e, d = -1, len(A)
  while e < d-1:
    m = (e + d) // 2
    if A[m] < x:
      e = m
    else:
      d = m
  return d

O que podemos dizer sobre o número de comparações A[m] < x no pior caso? Claramente, o pior caso novamente ocorre quando $x\not\in A$ ou quando é encontrado no último passo do laço. dada a natureza bisectante do algoritmo, o número de comparações realizadas é $O(\log n)$. Ou seja, é um algoritmo cujo consumo de tempo é logarítmico no número de elementos de $A$ — o que implica que a vasta maioria (para valores de $n$ grandes) dos elementos em $A$ não são inspecionados.

Obtenção do $O(\log n)$

Esta seção é opcional, apesar de ter sido feita em sala.

A título de simplificação (sem perda de generalidade), suponha que o número de elementos em $A$ é uma pontência de $2$. Isto é, $n=2^k$ para algum $k\geq 0$ inteiro. Seja $C(n)$ o número de comparações quando $A$ tem $n$ elementos. A cada passo do laço while, uma comparação é realizada e (neste caso), metade dos elementos são eliminados. Isto resulta em um problema de mesma natureza, mas com $n/2$ elementos. Quando $n=1$, uma comparação é realizada e o algoritmo termina no próximo passo.

Obtemos então, a recorrência $$C(n) = \begin{cases} C(n/2) + 1 & \text{se } n > 1, \\ 1 & \text{se } n = 1. \end{cases}$$

Para $n$ suficientemente grande, iterando a recorrência acima, obtemos $$\begin{align*} C(n) &= C(n/2^1) + 1 \\ &= C(n/2^2) + 1 + 1 = C(n/2^2) + 2 \\ &= C(n/2^3) + 1 + 2 = C(n/2^3) + 3 \\ &\;\;\vdots \\ &= C(n/2^j) + j. \end{align*}$$

Quando $n/2^j=2^k/2^j=1$, o que ocorre quando $j=k$, temos que $C(1)=1$ e, portanto, que $$C(n) = k+1.$$ Mas $n=2^k \iff k=\log_2 n$. Logo, $C(n) = 1 + \log_2 n = O(\log n)$.

Limitante Inferior *

Esta seção é opcional (e não foi feita em sala).

Pergunta natural: é possível fazer melhor, no pior caso? Em outras palavras, é possível achar um algoritmo que realize menos comparações do tipo A[m] < x que a busca binária, no pior caso, para o Problema 2.1?

A resposta é negativa! Mais do que isso: assintoticamente, a busca binária é ótima para o Problema 2.1. O argumento é baseado em um modelo computacional simples que realiza somente comparações, chamado árvores de decisão.

É conveniente definirmos o conceito de uma árvores binárias primeiro. Uma árvore binária $T$ é uma coleção de nós — cujo intento é armazenar dados ou representar eventos — organizada ordenada e hierarquicamente e definida como:

• $T$ é vazia, ou
• $T$ possui um nó dito raiz; este possui até dois descendentes diretos (filhos) — um esquerdo e um direito — que são árvores binárias. Denominamo-nas, respectivamente, de sub-árvores esquerda e direita à raiz.

Um nó em $T$ que não possui descendentes é chamado folha. A altura de um nó em $T$ é definida indutivamente como: a raiz tem altura $0$, as raízes das sub-árvores esquerda e direita tem altura $1$, e assim sucessivamente. A altura $h$ de $T$ é o máximo das alturas de seus nós — em outras palavras, o comprimento (número de nós menos $1$) de um caminho mais longo da raiz a uma folha de $T$. Caso $T=\emptyset$, sua altura é definida como $h=-1$. Não é difícil provar, por indução em $h$, que uma árvore binária não vazia possui no máximo $2^h$ folhas.

O cerne de qualquer algoritmo para o Problema 2.1 é a comparação entre os elementos em $A$ e $x$. Podemos codificar tais comparações como nós não folhas em uma árvore binária, armazenando conjuntamente a informação de qual sub-sequência de $A$ está sendo inspecionada no momento de cada comparação. Caso a comparação em um nó tenha sido positiva, codificamos o próximo passo do algoritmo em seu filho esquerdo; caso tenha sido negativa, em seu filho direito. Índices de $A$ devolvidos pelo algoritmo são codificados por folhas.

Uma tal árvore binária recebe o nome de árvore de decisão: partindo da raiz, realizando as comparações indicadas nos nós e seguindo os ramos correspondentes aos resultados (das comparações), mais cedo ou mais tarde atingimos uma folha com a resposta desejada.

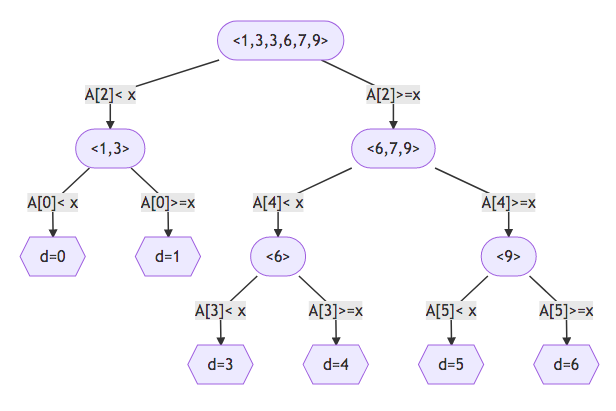
Como exemplo, apresentamos árvores de decisão para os algoritmos de busca sequencial ordenada e binária que desenvolvemos acima. Suponha que $A=[1,3,3,6,7,9]$ e que $x=2$. Temos que a árvore de decisão da busca sequencial é

e que a árvore de decisão da busca binária é

Observe que as duas tem estruturas bem diferentes. Em poucas palavras, a primeira é degenerada (quase um caminho) e tem altura de ordem linear; a segunda é mais regular e homogênea e tem altura de ordem logarítmica.

Tome alguns momentos, se necessário, para se convencer de que qualquer algoritmo de busca baseado em comparações — para quaisquer $A$ e $x$ — pode ser codificado como uma árvore de decisão.

Estar interessado no menor número de comparações no pior caso equivale, portanto, à altura da melhor árvore de decisão existente para o Problema 2.1 (claramente, estamos lidando com uma família infinita de árvores; uma para cada instância de entrada). Temos que qualquer índice em $\{0,1,\ldots,n\}$ pode ser devolvido como resposta. Logo, uma melhor árvore de decisão deve ter ao menos $n+1$ folhas.

Seja $T$ uma tal árvore com exatas $n+1$ folhas (suponha que ela existe). Como $T$ é binária, sua altura $h$ deve ser tal que $n+1\leq 2^h$, o que equivale a dizermos que $T$ deve ter altura $h\geq \log_2 (n+1)$. Em outras palavras, o número mínimo de comparações no pior caso para o Problema 2.1 é de ordem logarítmica.

Como a busca binária realiza $O(\log n)$ comparações no pior caso, a menos de constantes e termos de menor ordem (cada vez menos importantes à medida que $n\to\infty$), ela é ótima para o Problema 2.1.