Exercícios 1º passo, recorrência, transiência

Nos exercícios abaixo, sempre que necessário, considere $(X_n{)}_{n\ge 0}$$(X_n)_{n\geq 0}$ uma cadeia de Markov sobre o conjunto de estados $S$$S$ com transições $P$$P$ e distribuição inicial $\lambda$$\lambda$.

1. No jogo das apostas da lista de revisão e da lista da semana 2, suponha as jogadas CCC (cara-cara-cara) contra KCC (coroa-cara-cara) do segundo jogador. No seu modelo markoviano para esse jogo devem existir dois estados absorventes, um para cada jogador. Determine a probabilidade de absorção. Mostre que o tempo esperado de absorção é $7$$7$.

2. O diagrama abaixo representa uma cadeia de Markov com transições $p,q>0$$p,q>0$. Mostre os estados $i=1,2,3$$i=1,2,3$ são transientes verificando a desigualdade $\mathbb{P}(T_i=\mathrm{\infty }\mid X_0=1)>0$$\mathbb P (T_i = \infty\mid X_0=1)>0$.

3. Demonstre que, condicionado a $X_m=i$$X_m=i$, para eventos $A$$A$ da forma $[X_0=i_0,\dots ,X_m=i_m]$$[X_0=i_0,\dots,X_m=i_m]$ vale que

   $$\mathbb{P}([X_m=i_m,\dots ,X_{m+n}=i_{m+n}]\cap A\mid X_m=i)=\mathbb{P}(X_m=i_m,\dots ,X_{m+n}=i_{m+n}\mid X_m=i)\cdot \mathbb{P}(A\mid X_m=i)$$

   e conclua que o processo futuro $(X_{m+n}{)}_{n\ge 0}$$(X_{m+n})_{n\geq 0}$ é uma cadeia de Markov com transições $P$$P$ e estado inicial $i$$i$ (ou, distribuição inicial $({\delta }_{i,j}{)}_{j\in S}$$(\delta_{i,j})_{j\in S}$ – “delta de Kronecker” concentrado em $i$$i$), independente de $(X_0,X_1,\dots ,X_m)$$(X_0,X_1,\dots,X_m)$.

4. Defina a probabilidade de primeira passagem por $j$$j$ em exatamente $n$$n$ passos

   $$f_{ij}^{(n)}=\mathbb{P}(X_1\ne j,X_2\ne j,\dots ,X_{n-1}\ne j,X_n=j|X_0=i).$$

   (4.1) $f_{ij}^{(n)}=p_{ij}^n$$f_{ij}^{(n)} = p^n_{ij}$?

   (4.2) Se $T_i=min\{n>0:X_n=i\}$$T_i = \min\{n>0\colon X_n=i\}$ então $f_{ii}^{(n)}=\mathbb{P}(T_i=n\mid X_0=i)$$f_{ii}^{(n)} = \mathbb{P}(T_i=n\mid X_0=i)$?

   (4.3) Ainda, $f_{ii}=\mathbb{P}(T_i<\mathrm{\infty }\mid X_0=i)$$f_{ii} = \mathbb P(T_i<\infty\mid X_0=i)$ como definimos em aula. Então

   $$f_{ii}=\sum _{n=1}^{\mathrm{\infty }}{f}_{ii}^{(n)}=\sum _{n=1}^{\mathrm{\infty }}(f_{ii}{)}^n?$$

5. (Cobras e Escadas e uma Cadeia de Markov) 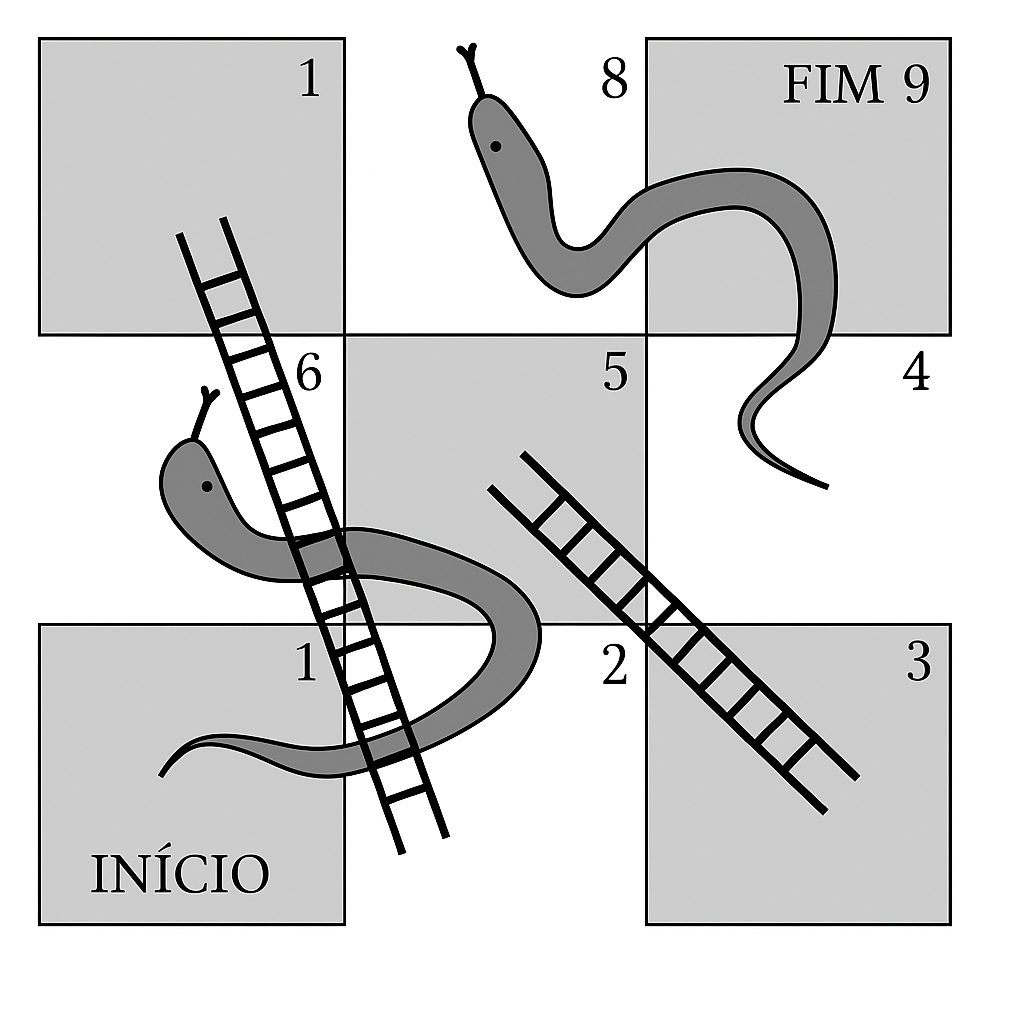Um jogo é jogado em um tabuleiro de nove casas. A cada jogada, o jogador lança uma moeda justa e avança uma ou duas casas, de acordo com o resultado ser cara ou coroa. Se o jogador parar no pé de uma escada, ele sobe até o topo; se parar na cabeça de uma cobra, ele desliza até a cauda.

   • Quantas jogadas, em média, são necessárias para completar o jogo?

   • Qual é a probabilidade de que um jogador que chegou à casa do meio termine o jogo sem escorregar de volta para a casa 1?

6. (Continuação de Ruína da lista anterior) Classifique os estados da cadeia. Considere o instante aleatório

   $$T=min\{n\ge 0:X_n=0\text{ ou }{X}_n=N\}.$$

   Deseja-se calcular a probabilidade de o jogador atingir $N antes de ir à falência, isto é,

   $$h(x)=\mathbb{P}(X_T=N\mid X_0=x),$$

   quando o jogo começa com fortuna inicial $X_0=x$$X_0 = x$. Explique por que $h(0)=0$$h(0) = 0$ e $h(N)=1$$h(N) = 1$. Usando o princípio da análise do primeiro passo, derive uma equação de recorrência para $h(x)$$h(x)$ quando $0<x<N$$0 < x < N$, considerando as possíveis evoluções do jogo na primeira jogada.

7. Seja $A\subseteq S$$A\subseteq S$ um subconjunto de estados e defina o tempo de parada $T_A=min\{n\ge 0:X_n\in A\}$$T_A= \min\{n\geq 0\colon X_n\in A\}$. O tempo médio de primeira passagem é dado por $m_i=\mathbb{E}[T_A\mid X_0=i]$$m_{i} = \mathbb{E}[T_A \mid X_0 = i]$. Demonstre que para $i\notin A$$i\not\in A$ vale

   $$m_i=1+\sum _{j\in S}{p}_{ij}{m}_j.$$