Avisos: P1 dia 03; soluções de alguns exercícios.
MCBM022-23 Introdução aos Processos Estocásticos
Jair Donadelli (sala 546, torre 2, bloco A) email jair.donadelli@ufabc.edu.br
Nessa disciplina vamos estudar os conceitos fundamentais de cadeias de Markov em tempo discreto e contínuo, martingais e teoria da renovação, com foco em suas propriedades, aplicações em modelagem e demonstrações teóricas. Calcular probabilidades de transição, retorno e limites, além de resolver e modelar situações-problema envolvendo esses temas.
onde: Seg. 21-23h; Qui. 19-21h na sala A-114-0
TPEI 4-0-0-4 RECOMENDAÇÃO: Álgebra Linear; Cálculo de Probabilidade
Atenção: todo comunicado do professor para os alunos será feito via Siga, portanto, atente-se ao seu endereço de email dessa plataforma. Não use o Siga para se comunicar com o professor, envie email para o endereço acima.
EMENTA Cadeias de Markov discretas e comportamento assintótico: passeios aleatórios, processo de ramificação. Processos de Poisson. Cadeias de Markov em tempo contínuo. Processos de renovação. Martingales. Introdução ao movimento browniano.
BIBLIOGRAFIA BÁSICA
ROSS, Sheldon M. Introduction to probability models. 10. ed. Burlington: Academic Press, 2010. xv, 784 p. ISBN 9780123756862.
DURRETT, Richard. Essentials of stochastic processes. New York: Springer, 1999. vi, 281 p. (Springer texts in statistics). ISBN 9780387988368.
HAIGH, John. Probability models. Falmer: Springer, 2002. viii, 256 p. (Springer undergraduate mathematics). ISBN 1852334312.
BIBLIOGRAFIA COMPLEMENTAR
GRIMMETT, Geoffrey; STIRZAKER, David. Probability and random processes. 3. ed. Oxford; New York: Oxford University Press, 2001. xii, 596 p. ISBN 9780198572220.
BHAT, U. Narayan; MILLER, Gregory K. Elements of applied stochastic processes. 3. ed. Hoboken: Wiley Publishing, 2002. xi, 461 p. (Wiley series in probability and statistics). ISBN 9780471414421.
TAYLOR, Howard M.; KARLIN, Samuel. An introduction to stochastic modeling. 3. ed. San Diego: Academic Press, 1998. xi, 631 p. ISBN 9780126848878.
RESNICK, Sidney I. Adventures in stochastic processes. Boston: Birkhäuser, 1992. xii, 626 p. ISBN 9780817635916.
MATERIAL BIBLIOGRÁFICO COMPLEMENTAR
Probability, Mathematical Statistics, Stochastic Processes
Finite Markov Chains and Algorithmic Applications
Markov Chains and Mixing Times
Cronograma das aulas
| Semana e Tema | Tópicos | Referências |
|---|---|---|
| Semana 1 – Introdução a Processos Estocásticos | - Plano de ensino - Conceitos de Probabilidade - Espaço de estados, tempo discreto vs. contínuo. | - Lista revisão de probabilidade - slide |
| Semana 2 – Introdução a Cadeias de Markov Discretas | - Propriedade de Markov e homogeneidade no tempo. - Matriz de transição | Ross, 4.1–4.2. G&S (Grimmet & Stirzaker), Cap. 6.1–6.2. - gerador de lero-lero - Exercícios |
| Semana 3 – Análise de primeiro passo. Propriedade Forte de Markov. Classificação de estados. | - Análise de primeiro passo. - Recorrência e transiência. - Estados absorventes. Probabilidade e tempo médio de absorção. | Ross, 4.2–4.3. G&S, Cap. 6.1. - Exercícios - Propriedade Forte de Markov |
| Semana 4 – Classificação de Estados e Cadeias. | - Propriedade Forte de Markov. - Tempo de primeira passagem e caracterização de recorrência e transiência. | Ross, Cap. 4.3–4.4. G&S, Cap. 6.2–6.3. - Exercícios |
| Semana 5 – Distribuições Invariantes | - Conjuntos fechados. Classes de comunicação. - Distribuição limite e distribuição estacionária. - Cadeias irredutiveis | Ross, Cap. 4.4. G&S, Cap. 6.4. - Exercícios |
| Semana 6 – Distribuições Invariantes e Convergência | - Cadeias aperiódicas. - Teorema ergódico (caso finito). | Idem Teorema ergódico |
| Semana 7 (feriado na 2ª) | Conteúdo até semana 05, inclusive | |
| Semana 8 | - Page rank - Passeio aleatório simples em - Cadeia de Ehrenfest | |
| Semana 9 – Martingais discretos | - Martingal, sub e supermartingal. - Propriedades básicas. - Teorema de parada opcional (forma simples). | Ross, Cap. 13.1–13.3. G&S, Cap. 12. |
| Semana 10 - Processos de Poisson(feriado na 5ª) | - Incrementos independentes e estacionários. - Distribuição de contagem (Poisson). - Distribuição de tempos (exponencial). - Superposição e divisão. | Ross, Cap. 5.1–5.3. G&S, Cap. 6.10. |
| Semana 11–Processos de Poisson | idem | idem |
| Semana 12 – Avaliação | Conteúdo a partir da P1 | |
| Semana de reposição - Recuperação | Todo conteúdo |
Avaliação
2 provas. As avaliações são individuais. Serão atribuídos conceitos nas atividades avaliativas e o resultado é definido como segue:

Substitutiva e Recuperação
A sub é aberta a qualquer aluno.
Tem direito ao exame recuperação aqueles que foram aprovado com D ou reprovado com F e obtiveram frequência mínima. O resultado do exame é um conceito que compõe com o conceito final M obtido na avaliação regular da disciplina como segue:
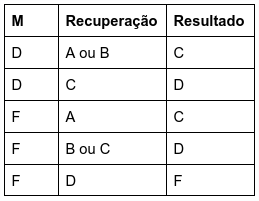
O aluno deve manifestar interesse em fazer a recuperação de acordo com as instruções que serão enviadas por email em momento apropriado durante o curso da disciplina.
Atendimento
2ª 20hs e 5ª 21hs ou qualquer outro horário combinado previamente.
